这场没打啊
A. Diagonal Walking
签到
B. String Typing
签到
C. Matrix Walk
题意
给一个x*y的矩阵A,对于每个 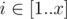 ,
, 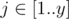 Ai, j = y(i - 1) + j,矩阵中的格子一步可以走到相邻的格子,现给出路径序列,问y的大小,以及路径是否合理
Ai, j = y(i - 1) + j,矩阵中的格子一步可以走到相邻的格子,现给出路径序列,问y的大小,以及路径是否合理
分析
分析可知相邻两个点差值的绝对值不为1的话,则为y
只要注意一下,
1 2 3
4 5 6, 3->4 / 4->3 这两种不可一步互相到达即可
D. Fight Against Traffic
题意
给一个n个点,m条边的无向图,给定起点s,终点t,问现增加一条边使得s到t的最短路不变的方案数(n,m<=1e3 )
分析
最短路?(X)
分别从s和t跑一次bfs,记录下所有点到s和t的距离,枚举所有没有给的边,check一下即可
check:如果加的这条边使得s到t的最短路变小,则一定经过这条边,只需枚举一下边的端点即可

#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<queue>
#include<map>
#include<vector>
#include<set>
#include<ctime>
#include<bits/stdc++.h>
#define LL long long
#define db double
#define EPS 1e-15
#define inf 1e16
#define pa pair<int,int>
using namespace std;
const int maxn = 1000+5;
int ds[maxn], dt[maxn];
int n,m,s,t;
vector<int>g[maxn];
bool vis[maxn];
int mp[maxn][maxn];
void bfs(int ss)
{
memset(vis,0,sizeof(vis));
vis[ss]=1;
ds[ss]=0;
queue<int>q;
while(!q.empty())
q.pop();
q.push(ss);
while(!q.empty())
{
int u=q.front();
q.pop();
for(int i=0;i<int(g[u].size());i++)
{
if(!vis[g[u][i]])
{
vis[g[u][i]]=1;
ds[g[u][i]]=ds[u]+1;
q.push(g[u][i]);
}
}
}
}
void bfsa(int tt)
{
memset(vis,0,sizeof(vis));
vis[tt]=1;
dt[tt]=0;
queue<int>q;
while(!q.empty())
q.pop();
q.push(tt);
while(!q.empty())
{
int u=q.front();
q.pop();
for(int i=0;i<int(g[u].size());i++)
{
if(!vis[g[u][i]])
{
vis[g[u][i]]=1;
dt[g[u][i]]=dt[u]+1;
q.push(g[u][i]);
}
}
}
}
int main()
{
int u, v;
scanf("%d%d%d%d", &n, &m, &s, &t);
for(int i=1;i<=m;i++)
{
scanf("%d%d", &u, &v);
g[u].push_back(v);
g[v].push_back(u);
mp[u][v]=mp[v][u]=1;
}
bfs(s);
bfsa(t);
int cnt=0;
for(int i=1;i<=n;i++)
{
for(int j=i+1;j<=n;j++)
{
if(!mp[i][j])
{
if((ds[i]+dt[j]+1)>=ds[t] && (dt[i]+ds[j]+1)>=ds[t])
cnt++;
}
}
}
printf("%d
" ,cnt);
return 0;
}
E. Water Taps
题意
分析
F. Runner's Problem
题意
分析
G. Castle Defense
题意
分析
