浙大《数据结构》第六章：图(上)

注：本文使用的网课资源为中国大学MOOC

https://www.icourse163.org/course/ZJU-93001

目录

• 什么是图(Graph)
  • 抽象数据类型定义
  • 怎么在程序中表示一个图
• 图的遍历
  • 深度优先搜索(DFS)
  • 广度优先搜索(BFS)
  • 如果图不连通怎么办？
• 应用实例：拯救007
  • 题意理解
  • 解题思路
  • 程序实现
• 应用实例：六度空间
  • 题意理解
  • 解题思路

什么是图(Graph)

表示“多对多”的关系

包含：

• 一组顶点：通常由V(vertex)表示顶点集合
• 一组边：通常用E(edge)表示边的集合
  1. 边是顶点对：((v,w) in E),其中(v,w in V)
  2. 有向边<v,w>表示从v指向w的边(单行线)
  3. 不考虑重边和自回路

抽象数据类型定义

类型名称：图(graph)

数据对象集：G(V,E)由一个非空的有限顶点集合V和一个有限边集合E组成。

操作集：对于任意的图(G in Graph)，以及(v in V, e in E)。常见的操作有：

 Graph Create(); // 建立并返回空图
 Graph InsertVertex( Graph G, Vertex v ); // 将顶点v插入G
 Graph InsertEdge( Graph G, Edge e ); // 将边e插入G
 void DFS( Graph G, Vertex v ); // 从顶点v除法深度优先遍历图G
 void BFS( Graph G, Vertex v ) // 从顶点v出发宽度优先遍历图G
 void ShortestPath( Graph G, Vertex v, int Dist[] ); // 计算图G中顶点v到任意其他顶点的最短距离
 void MST( Graph G ); // 计算图G的最小生成树

怎么在程序中表示一个图

用邻接矩阵表示

G[N][N] --- N个顶点从0到N-1编号

[G[i][j] = egin{cases} 1, & ext{若}<v_i,v_j> ext{ 是G中的边} \ 0, & ext{否则} end{cases} ]

1、对于无向图的存储，怎样省一半空间？

答：用一个长度为N(N+1)/2的一维数组A存储{(G_{00},G_{10},G_{11},...,G_{n-1,0},...,G_{n-1,n-1})}，则(G_{ij})在A中对应的下标是：

[(i*(i+1)/2+j) ]

2、对于网络(带权重的图)，只要把G[i][j]的值由(0,1)定义为(<v_i,v_j>)的权重即可。

3、邻接矩阵的好处：

• 直观、简单
• 方便检查任意一对顶点是否存在边
• 方便找任一顶点的所有“邻接点”（有边直接相连的顶点）
• 方便计算任一顶点的“度”（从该点发出的边数为“出度”，指向该点的边数为“入度”）
  1. 无向图：对应行（或列）非0元素的个数。
  2. 有向图：对应行非0元素的个数是“出度”；对应列非0元素的个数是“入度”。

4、邻接矩阵的缺点：

• 浪费空间：存稀疏图有大量的无效元素，对稠密图(特别是完全图)还是很划算
• 浪费时间：统计稀疏图中一共有多少条边时需要全局扫描。

邻接矩阵程序实现

/* 图的邻接矩阵表示法 */
 
#define MaxVertexNum 100    /* 最大顶点数设为100 */
#define INFINITY 65535      /* ∞设为双字节无符号整数的最大值65535*/
typedef int Vertex;         /* 用顶点下标表示顶点,为整型 */
typedef int WeightType;     /* 边的权值设为整型 */
typedef char DataType;      /* 顶点存储的数据类型设为字符型 */

/* 边的定义 */
typedef struct ENode *PtrToENode;
struct ENode{
    Vertex V1, V2;      // 有向边<V1, V2>
    WeightType Weight;  // 权重 
};
typedef PtrToENode Edge;

/* 图结点的定义 */
typedef struct GNode *PtrToGNode;
struct GNode
{
    int Nv;  // 顶点数
    int Ne;  // 边数
    WeightType G[MaxVertexNum][MaxVertexNum]; // 邻接矩阵
    DataType Data[MaxVertexNum]; // 存顶点的数据，若顶点无数据，则不需要出现Data[]
}
typedef PtrToGNode MGraph; // 以邻接矩阵存储的图类型


/* 初始化一个有VertexNum个顶点但没有边的图 */
MGraph CreateGraph( int VertexNum )
{ 
    Vertex V, W;
    MGraph Graph;
     
    Graph = (MGraph)malloc(sizeof(struct GNode)); // 建立图
    Graph->Nv = VertexNum;
    Graph->Ne = 0;
    /* 初始化邻接矩阵 */
    /* 注意：这里默认顶点编号从0开始，到(Graph->Nv - 1) */
    for (V=0; V < Graph->Nv; V++)
        for (W=0; W < Graph->Nv; W++)  
            Graph->G[V][W] = INFINITY;
             
    return Graph; 
}

/* 向MGraph中插入边 */
void InsertEdge( MGraph Graph, Edge E )
{
    /* 插入边 <V1, V2> */
    Graph->G[E->V1][E->V2] = E->Weight;    
    /* 若是无向图，还要插入边<V2, V1> */
    //Graph->G[E->V2][E->V1] = E->Weight;
}

/* 完整地建立一个MGraph */
/* 输入格式：
Nv Ne (边数和顶点个数)
V1 V2 Weight
....... (依次输入边的起点，终点，和权重) */
MGraph BuildGraph()
{
    MGraph Graph;
    Edge E;
    Vertex V;
    int Nv, i;
     
    scanf("%d", &Nv);   // 读入顶点个数
    Graph = CreateGraph(Nv); // 初始化有Nv个顶点但没有边的图
     
    scanf("%d", &(Graph->Ne)); // 读入边数
    if ( Graph->Ne != 0 ) 
    { 
        /* 如果有边 */ 
        E = (Edge)malloc(sizeof(struct ENode)); // 建立边结点 
        /* 读入边，格式为"起点 终点 权重"，插入邻接矩阵 */
        for (i=0; i<Graph->Ne; i++) 
        {
            scanf("%d %d %d", &E->V1, &E->V2, &E->Weight); 
            /* 注意：如果权重不是整型，Weight的读入格式要改 */
            InsertEdge( Graph, E );
        }
    } 
 
    /* 如果顶点有数据的话，读入数据 */
    for (V=0; V < Graph->Nv; V++) 
        scanf(" %c", &(Graph->Data[V]));
 
    return Graph;
}

用邻接表表示

邻接表：G[N]为指针数组，对应矩阵每行一个链表，只存非0元素。（对于网络，结构中要增加权重的域）。如图所示：

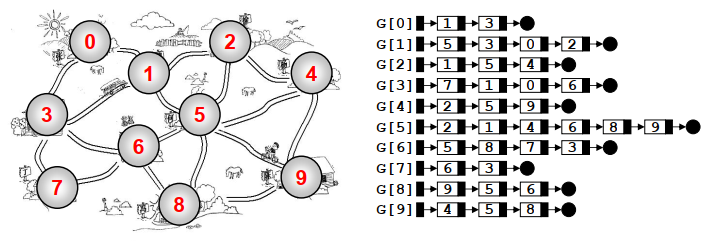
1、邻接表的好处：

• 方便找任一顶点的所有邻接点；
• 节约稀疏图的空间，但是需要N个头指针 + 2E个结点(每个结点至少2个域)
• 方便计算任一顶点的度？
  1. 对于无向图：是的
  2. 对于有向图：只能计算“出度”；需要构造“逆邻接表”（存指向自己的边）来方便计算“入度”。

2、邻接表的缺点：

• 不能检查任意一对顶点间是否存在边。

邻接表程序实现

/* 图的邻接表表示法 */
 
#define MaxVertexNum 100    /* 最大顶点数设为100 */
typedef int Vertex;         /* 用顶点下标表示顶点,为整型 */
typedef int WeightType;     /* 边的权值设为整型 */
typedef char DataType;      /* 顶点存储的数据类型设为字符型 */

/* 边的定义 */
typedef struct ENode *PtrToENode;
struct ENode{
    Vertex V1, V2;      // 有向边<V1, V2> /
    WeightType Weight;  // 权重
};
typedef PtrToENode Edge;

/* 邻接点的定义 */
typedef struct AdjVNode *PtrToAdjVNode;
struct AdjVNode
{
    Vertex AdjV;        // 邻接点下标
    WeightType Weight;  // 权重
    PtrToAdjVNode Next; // 指向下一个邻接点的指针
}

/* 顶点表头结点的定义 */
typedef struct Vnode
{
    PtrToAdjVNode FirstEdge; // 边表头指针
    DataType Data;            // 存顶点的数据 
    /* 注意：很多情况下，顶点无数据，此时Data可以不用出现 */
} AdjList[MaxVertexNum];    /* AdjList是邻接表类型 */

/* 图结点的定义 */
typedef struct GNode *PtrToGNode;
struct GNode
{
    int Nv;     // 顶点数
    int Ne;     // 边数
    AdjList G;  // 邻接表
}
typedef PtrToGNode LGraph; /* 以邻接表方式存储的图类型 */


/* 初始化一个有VertexNum个顶点但没有边的图 */
LGraph CreatGraph( int VertexNum )
{
    Vertex V, W;
    LGraph Graph;
    
    Graph = (LGraph)malloc(sizeof(struct GNode));
    Graph->Nv = VertexNum;
    Graph->Ne = 0;
    
    
    /* 注意：这里默认顶点编号从0开始，到(Graph->Nv - 1) */
    for (V=0; V < Graph->Nv; V++)
        Graph->G[V].FirstEdge = NULL;
    
    return Graph;
}

/* 向LGraph中插入边 */
void InsertEdge(  LGraph Graph, Edge E )
{
    PtrToAdjVNode NewNode;
    
    /***************** 插入边 <V1, V2> ****************/
    /* 为V2建立新的邻接点 */
    NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
    NewNode->AdjV = E->V2;
    NewNode->Weight = E->Weight;
    /* 将V2插入V1的表头 */
    NewNode->Next = Graph->G[E->V1].FirstEdge;
    Graph->G[E->V1].FirstEdge = NewNode;
    
    /********** 若是无向图，还要插入边 <V2, V1> **********/
    /* 为V1建立新的邻接点 */
    NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
    NewNode->AdjV = E->V1;
    NewNode->Weight = E->Weight;
    /* 将V1插入V2的表头 */
    NewNode->Next = Graph->G[E->V2].FirstEdge;
    Graph->G[E->V2].FirstEdge = NewNode;
}

/* 完整地建立一个LGraph */
LGraph BuildGaph()
{
    LGraph Graph;
    Edge E;
    Vertex V;
    int Nv, i;
     
    scanf("%d", &Nv);   // 读入顶点个数
    Graph = CreateGraph(Nv); // 初始化有Nv个顶点但没有边的图
     
    scanf("%d", &(Graph->Ne));   // 读入边数
    if ( Graph->Ne != 0 ) 
    { 
        /* 如果有边 */ 
        E = (Edge)malloc( sizeof(struct ENode) ); // 建立边结点
        /* 读入边，格式为"起点 终点 权重"，插入邻接矩阵 */
        for (i=0; i<Graph->Ne; i++) {
            scanf("%d %d %d", &E->V1, &E->V2, &E->Weight); 
            /* 注意：如果权重不是整型，Weight的读入格式要改 */
            InsertEdge( Graph, E );
        }
    } 
 
    /* 如果顶点有数据的话，读入数据 */
    for (V=0; V<Graph->Nv; V++) 
        scanf(" %c", &(Graph->G[V].Data));
 
    return Graph;
}

图的遍历

深度优先搜索(DFS)

类似于树的先序遍历，它沿着树的深度，遍历树的结点，极可能深地搜索树的分支，当结点V的所有边都已被探寻过，搜索将回溯到发现结点V的那条边的起始结点，假设有如下二叉树。

      A          
    /            
   B     C     
  /    /               
 D   E F   G 

A是第一个访问的，然后顺序是B,D，然后是E，接着再是CFG。

若有N个顶点，E条边，时间复杂度是：

• 用邻接表存储图，有O(N+E)
• 用邻接矩阵存储图，有O(N^2)

/* DFS */
/* 输入：
   Graph：已知图，V：起始顶点，VertexNum：顶点数，visited：用于标记的数组
*/
void ArrayGraph_DFS( MGraph Graph, Vertex V, int VertexNum, bool visited[] )
{
    int i;
    printf("%c	",Graph->Data[V]);///先输出起始顶点，再输出访问的其他顶点
    visited[V]=true;///事先将起始顶点标记为true
    
    for (i=0; i<VertexNum; i++) // 遍历n的每个邻接点
    {
        if (Graph->G[V][i]!=0 && visited[i]==0)  // 若第i个顶点与Graph->G[n]有关，并且未被访问
            ArrayGraph_DFS(Graph,i,VertexNum,visited); //用递归的方式继续搜寻
    }
}

广度优先搜索(BFS)

类似于树的层次遍历，从根节点开始，沿着树的宽度遍历树的节点。如果所有节点均被访问，则算法中止。

      A          
    /            
   B     C     
  /    /               
 D   E F   G 

这里A是第一个访问的，然后顺序是 B、C，然后再是 D、E、F、G。可以借助队列结构实现BFS访问。

若有N个顶点，E条边，时间复杂度是

• 用邻接表存储，O(N+E)
• 用邻接矩阵存储，O(N^2)

/* BFS */
/* 输入：
   Graph：已知图，V：起始顶点，VertexNum：顶点数，visited：用于标记的数组
*/
void ArrayGraph_BFS( MGraph Graph, Vertex V, int VertexNum )
{
    int i;
    int visited[MAXN]; // visited数组用于标记顶点是否被访问
    for (i=0; i<a; i++) // 对visited数组进行初始化，0为未访问，1为以访问，避免在搜寻过程中碰见闭环
        visited[i]=0;
    int flag=0; // flag为标记变量，用于防止出现两个或以上的连通分量导致的图为搜寻完成。
    queue<Vertex> Q;
    int tou; // 代表队首位置元素
    while(!flag)
    {
        printf(" %c 	",G->Data[V]);
        visited[V]=1; // 将起始位置标记为已访问
        Q.push(V); // 起始顶点入队列
        
        while ( !Q.empty() ) // 当队列不为空时，循环操作
        {
            tou = Q.front(); // 取队首位置元素 Q.pop(); // 将队首出队列
            for (i=0; i<VertexNum; i++) // 遍历n的每个邻接点
            {
                if ( Graph->G[tou][i]!=0 && visited[i]==0 )
                {
            	    visited[i] = 1; // 标记已访问
            	    Q.push(i); // 入列
                }
            }
        }
        flag=1; // 将flag标记为1，当顶点全部访问完成则结束循环，否则循环继续
        for (i=0 i<VertexNum; i++)
        {
            if ( visited[i]==0 ) // 此循环用于判断顶点是否访问完成
            {
                flag=0;
                n=i;
                break;
            }
        }
    }
}

如果图不连通怎么办？

连通：如果从v到w存在一条(无向)路径，则称v和w是连通的。

路径：v到w的路径是一系列顶点{(V, v_1,v_2, ...,v_n, W)}的集合，其中任一对相邻的顶点间都有图中的边，路径的长度是路径中的边数(如果带权，则是所有边的权重和)。如果v到w之间的所有顶点都不同，则称简单路径。

回路：起点等于终点的路径

连通图：途中任意两顶点均连通。

连通分量：无向图的极大连通子图

• 极大顶点数：再加1个顶点就不连通了
• 极大边数：包含子图中所有顶点相连的所有边。

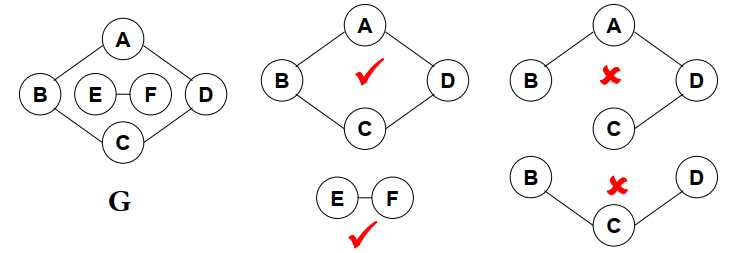
强连通：有向图中顶点v和w之间存在双向路径，则称v和w是强连通的

强连通图：有向图中任意两顶点均强连通

强连通分量：有向图的极大强连通子图

应用实例：拯救007

题意理解

假设湖是一个100乘100的正方形。 假设湖的中心在（0,0），东北角在（50,50）。中央岛是直径为15，以（0,0）为中心的圆盘。许多鳄鱼在湖的不同位置。考虑到每个鳄鱼的坐标和詹姆斯可以跳跃的距离，你必须告诉他他是否可以逃脱。

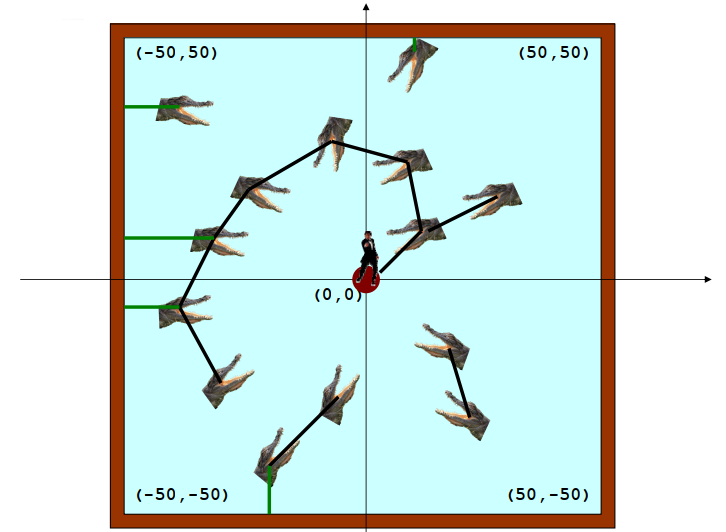
输入格式

首先第一行给出两个正整数：鳄鱼数量 N（≤100）和007一次能跳跃的最大距离 D。随后 N 行，每行给出一条鳄鱼的 (x,y) 坐标。注意：不会有两条鳄鱼待在同一个点上。

输出格式

如果007有可能逃脱，就在一行中输出"Yes"，否则输出"No"。

Sample Input

14 20
25 -15
-25 28
8 49
29 15
-35 -2
5 28
27 -29
-8 -28
-20 -35
-25 -20
-13 29
-30 15
-35 40
12 12

Sample Output

Yes

解题思路

利用DFS,遍历全部能"开始一步跳上"的鳄鱼，即每个连通图，如果遇到某个鳄鱼 “能上岸”，即退出遍历，输出“Yes”，如果全部连通图都遍历完成，还是不能上岸，则输出“No”。

程序实现

#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#include <WinDef.h>
#define MaxVertexNum 101 /* 最大顶点数设为101 */

struct Crocodile
{
    int x;
    int y;
    BOOL Isvisit;      // 是否被访问
} cro[MaxVertexNum];   //存储鳄鱼坐标的数据结构

int N; // 鳄鱼数
int D; // 跳跃距离


/*************函数声明**************/
double Distance(int i, int j);
BOOL CanEscape(int i);
BOOL DFS(struct Crocodile cro[], int V);


/**********************************/
/*             主函数             */
/*********************************/
int main()
{
    BOOL result = FALSE; //存储结果，是否能逃脱
    scanf("%d %d", &N, &D);

    cro[0].x = 0; //下标为0的结点为小岛
    cro[0].y = 0;
    cro[0].Isvisit = TRUE;

    /*  输入鳄鱼坐标   */
    for (int i = 1; i <= N; i++) 
        scanf("%d %d", &cro[i].x, &cro[i].y);

    for (int i = 1; i <= N; i++)
    {

        if (Distance(0, i) <= (D + 7.5)) //从小岛跳到鳄鱼上
        {
            result = DFS(cro, i);
            if (result)
            {
                printf("Yes
");
                break;
            }
        }
    }
    if (!result)
        printf("No
");

    system("pause"); //程序暂停，显示按下任意键继续
    return 0;
}

/***********************************/
/*         计算两个鳄鱼的距离       */
/* INPUT: i    ——代表第i个鳄鱼坐标  */
/*        j    ——代表第j个鳄鱼坐标  */
/* RETURN: 两个鳄鱼的直线距离       */
/***********************************/
double Distance(int i, int j)
{
    double b;
    b = sqrt(pow(cro[i].x - cro[j].x, 2) + pow(cro[i].y - cro[j].y, 2));
    return b;
}

/***********************************/
/* 判断是否能从当前鳄鱼跳一次就否脱离 */ 
/* INPUT: i    ——鳄鱼的编号         */
/* RETURN: 能则TRUE,不能则是FALSE   */
/***********************************/
BOOL CanEscape(int i)
{
    // 分别计算当前结点与岸边的距离
    // 即与 (x,50),(x,-50),(50,y),(-50,y) 的距离
    if (abs(cro[i].x - 50) <= D || abs(cro[i].x + 50) <= D 
        || abs(cro[i].y + 50) <= D || abs(cro[i].y - 50) <= D)
        return TRUE; // 如果该鳄鱼位置和"岸边"相邻，将情况置为 TRUE
    return FALSE;
}

/************************************/
/*             深度搜索              */
/* INPUT: cro    ——鳄鱼的结点      */
/*        V      ——当前鳄鱼的标号  */
/* RETURN: 能则TRUE,不能则是FALSE    */
/************************************/
BOOL DFS(struct Crocodile cro[], int V)
{
    BOOL result = FALSE;    // 存储结果，是否能逃脱
    cro[V].Isvisit = TRUE;  // 当前坐在的鳄鱼
    if (CanEscape(V))       // 出口条件
        result = TRUE;
    else
    { //递归部分
        for (int i = 1; i <= N; i++)
        {
            if ((cro[i].Isvisit == FALSE) && (Distance(V, i) <= D)) //当没有访问过且能跳过去
                result = DFS(cro, i);
        }
    }
    return result;
}

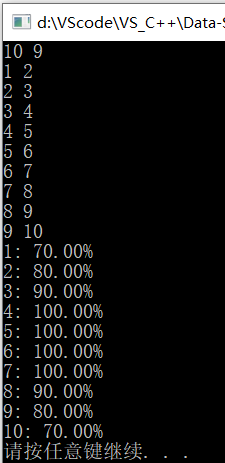
运行结果

应用实例：六度空间

题意理解

你和任何一个陌生人之间所间隔的人不会超过六个，给定社交网络图，请对每个节点计算符合“六度空间”理论的结点占结点总数的百分比。

输入格式

输入第1行给出两个正整数，分别表示社交网络图的结点数N（(1<N le 10^4),表示人数），边数M（(le 33*N)，表示社交关系数）。随后的M行对应M条边，每行给出一对正整数，分别是该条边直接连通的两个结点的编号（节点从1到N编号）。

输出格式
对每个结点输出与该结点距离不超过6的结点数占结点总数的百分比，精确到小数点后2位。每个结节点输出一行，格式为“结点编号:（空格）百分比%”。

Sample Input

10 9
1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 9
9 10

Sample Output

1: 70.00%
2: 80.00%
3: 90.00%
4: 100.00%
5: 100.00%
6: 100.00%
7: 100.00%
8: 90.00%
9: 80.00%
10: 70.00%

解题思路

• 对节点进行广度优先搜索
• 搜索过程中累计访问的节点数
• 需要记录“层数”，仅计算6层以内的节点数
• 边数 M 最大是顶点数 N 的 33 倍，很容易成为"稀疏图"，为了节省空间，采用邻接表方式存储
• BFS 适合统计步数，选用 BFS 对图遍历
• 为了节省空间，统计步数使用3个变量
  1. level，记录当前层数，如果 level=6 结束循环返回
  2. tail，记录当前入队元素，每遍历一个结点就更新一次，入队元素肯定是当前出队元素的下一层，当必要时，更新 last 为 tail，就记录了下一层的最后一个数
  3. last，记录当前层，当前层最后一个数，当当前出队元素v与 last 相等，说明该层遍历完成，更新 last = tail

如图所示：

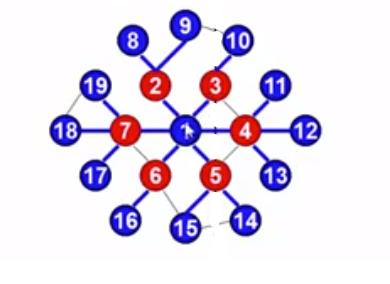
首先访问顶点1，顶点1入队，因为1所在0层，所以此时level=0.同时1是第0层入队的最后一个元素，所以 last=1 ;

然后让顶点1出队，按编号从小到大访问1的邻接点2,3,4,5,6,7，每访问一个邻接点就将值赋给tail,所以此时 tail=7 ,当1的邻接点访问完毕，last=1,说明第0层入队的元素已经都访问完毕，且第0层所有的元素的邻接点都已访问完毕，即第1层也被访问完毕，此时level++，且让last更新为tail。

依次类推，当 level=6 时，直接退出BFS。

#include <iostream> /* 引入命名空间，以及模块化I/O */
#include <queue>    /* 引用队列，常用函数有empty，push，front，back，pop，size */
#include <stdio.h>
#include <stdlib.h>

using namespace std;

#define MAXV 1005

/***********全局变量***********/
typedef int vertex;
typedef struct Node *AdjList;
struct Node
{
    vertex Adjv;    // 当前下标
    AdjList Next;   // 下一个
};
AdjList G[MAXV];    // 使用邻接表来构建图
bool Isvisit[MAXV]; // 是否访问
int N;              // 图的结点数
int M;              // 图的边数

/***********函数声明***********/
int BFS(vertex v);  // 起始点为v的BFS搜索
void SDS();         // 六度空间查找

/**********************************/
/*             主函数              */
/**********************************/
int main()
{
    vertex v1, v2;  // 图的顶点
    AdjList NewNode;

    scanf("%d%d", &N, &M);

    // 初始化点，从 1—N
    for (int i = 1; i <= N; i++)
    {
        G[i] = (AdjList)malloc(sizeof(struct Node));
        G[i]->Adjv = i;
        G[i]->Next = NULL;
    }

    // 初始化边
    for (int i = 0; i < M; i++)
    {
        scanf("%d%d", &v1, &v2);
        NewNode = (AdjList)malloc(sizeof(struct Node));
        NewNode->Adjv = v2;
        NewNode->Next = G[v1]->Next;
        G[v1]->Next = NewNode;

        NewNode = (AdjList)malloc(sizeof(struct Node));
        NewNode->Adjv = v1;
        NewNode->Next = G[v2]->Next;
        G[v2]->Next = NewNode;
    }
    
    // 运行主函数算法
    SDS();

    system("PAUSE");
    return 0;
}

/***********************************/
/*           广度优先搜索           */
/* INPUT: v ——广度优先搜索的起始点  */
/* RETURN: 符合六度空间的顶点个数    */
/***********************************/
int BFS(vertex v)
{
    int last, tail, level; // 三个辅助变量
    vertex W;
    AdjList node;

    queue<int> q; // 定义队列q
    Isvisit[v] = true;
    int count = 1; // 计数器初始值为1

    q.push(v);
    level = 0;
    last = v; //第0层最后一个入队的元素是v
    /*进入核心循环*/
    while (!q.empty())
    {
        W = q.front();
        q.pop();

        // G[i]第一个结点存自己的下标
        node = G[W]->Next;
        while (node)
        {
            if (!Isvisit[node->Adjv])
            {
                Isvisit[node->Adjv] = true;
                q.push(node->Adjv);
                count++;
                tail = node->Adjv; // 每次更新该结点
            }
            node = node->Next;
        }
        // 如果该当前结点是这层最后一个结点
        if (W == last)
        {
            level++;     // 层数 +1
            last = tail; // 更改 last
        }
        // 层数够了结束
        if (level == 6)
            break;
    }
    return count;
}

/***********************************/
/*           六度空间查找           */
/***********************************/
void SDS()
{
    int count;
    for (vertex v = 1; v <= N; v++)
    {
        // 由于要重复查找，需要将Isvisit序列填充为false，长度为MAXV
        fill(Isvisit, Isvisit + MAXV, false); 
        count = BFS(v);
        printf("%d: %.2f%%
", v, count * 100.0 / N);
    }
}

运行结果