1454E Number of Simple Paths

题目传送门

经典没读懂题瞎推一波样例求不出来安详入睡

题意

　　无向图，n个点，n个边，求图中任意一个点到另一个点的不重复路径总数。拿下图举例:

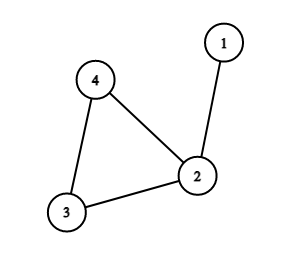
【1，2，3，4】和【1，2，4，3】是不重复的两条路径。而【1，2，3，4】和【4，3，2，1】重复了。

n个点的树有n-1条边,若再加一条边，则会形成一个环，除了环之外，其余部分由若干子树构成。  ==>   基环树。

对于无向图，拓扑排序处理出环，再处理出环上每个节点分支上的的节点个数。

设 ans=n*(n-1)  ,这是所有节点都在环上的情况，每个节点到另一个节点有两条路径。

如果环上某个节点分支上有若干个节点，那么这个分支上的路径数实际是重复的，设 cnt 为环上某个节点分支上的节点总数，则重复路径数为 C²_cnt  ，asn 减去重复路径数即为总路径数。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int inf =0x3f3f3f3f;
const int qs=2e5+7;
vector<ll> v[qs];
ll t,n,in[qs];
bool u[qs];
void topsort(){    //拓扑排序处理环 
    queue<ll> q;
    for(int i=1;i<=n;++i) if(in[i]==1) q.push(i);
    while(q.size()){
        ll t=q.front(); q.pop();
        u[t]=1;
        int Si=v[t].size();
        for(int i=0;i<Si;++i){
            int x=v[t][i];
            if(in[x]>1){
                in[x]--;
                if(in[x]==1) q.push(x);
            }
        }
    }
}
ll dfs(int x,int fa){   //dfs求环上节点分支上节点总数 
    ll Si=v[x].size(),res=0;
    for(int i=0;i<Si;++i){
        ll fx=v[x][i];
        if(u[fx]&&fx!=fa){
            res+=dfs(fx,x);
            res++;
        }
    }
    return res;
}
ll cal(ll x){        // 排列组合 去重 
    return x*(x-1)/2;
}
int main(){
    std::ios::sync_with_stdio(false);
    cin>>t;
    while(t--){
        cin>>n;
        for(int i=0;i<=n;++i){
            v[i].clear(); in[i]=u[i]=0;
        }
        int x,y;
        for(int i=1;i<=n;++i){
            cin>>x>>y;
            v[x].push_back(y); in[x]++;
            v[y].push_back(x); in[y]++;
        }
        topsort();
        ll ans=n*(n-1);        //最好情况下的总路径数 
        for(int i=1;i<=n;++i){
            if(!u[i]){
                ll cnt=dfs(i,0);
                ans-=cal(cnt+1);    //去重 
            }
        }
        cout<<ans<<"
";
    }
    return 0;
}