迭代方法图(图 1)包含一个标题为“计算参数更新”的华而不实的绿框。现在,我们将用更实质的方法代替这种华而不实的算法。
假设我们有时间和计算资源来计算 w1 的所有可能值的损失。对于我们一直在研究的回归问题,所产生的损失与 w1 的图形始终是凸形。换言之,图形始终是碗状图,如下所示:
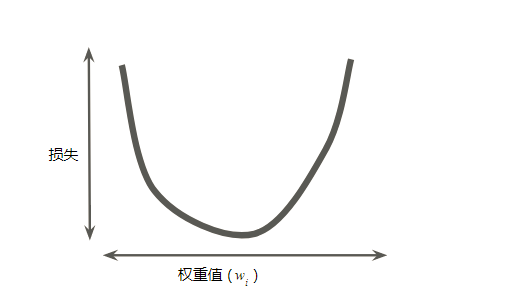
图 2. 回归问题产生的损失与权重图为凸形。
凸形问题只有一个最低点;即只存在一个斜率正好为 0 的位置。这个最小值就是损失函数收敛之处。
通过计算整个数据集中 w1 每个可能值的损失函数来找到收敛点这种方法效率太低。我们来研究一种更好的机制,这种机制在机器学习领域非常热门,称为梯度下降法。
梯度下降法的第一个阶段是为 w1 选择一个起始值(起点)。起点并不重要;因此很多算法就直接将 w1 设为 0 或随机选择一个值。下图显示的是我们选择了一个稍大于 0 的起点:
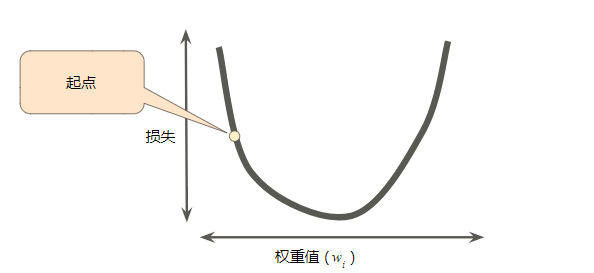
图 3. 梯度下降法的起点。
然后,梯度下降法算法会计算损失曲线在起点处的梯度。简而言之,梯度是偏导数的矢量;它可以让您了解哪个方向距离目标“更近”或“更远”。请注意,损失相对于单个权重的梯度(如图 3 所示)就等于导数。
详细了解偏导数和梯度。
请注意,梯度是一个矢量,因此具有以下两个特征:
- 方向
- 大小
梯度始终指向损失函数中增长最为迅猛的方向。梯度下降法算法会沿着负梯度的方向走一步,以便尽快降低损失。
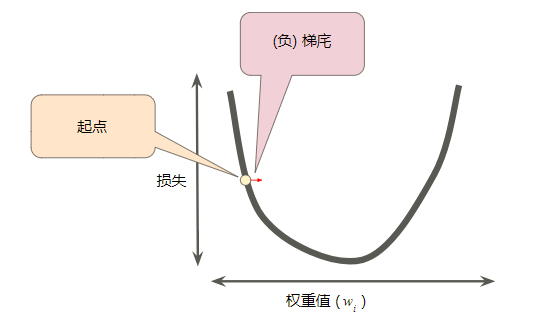
图 4. 梯度下降法依赖于负梯度。
为了确定损失函数曲线上的下一个点,梯度下降法算法会将梯度大小的一部分与起点相加,如下图所示:
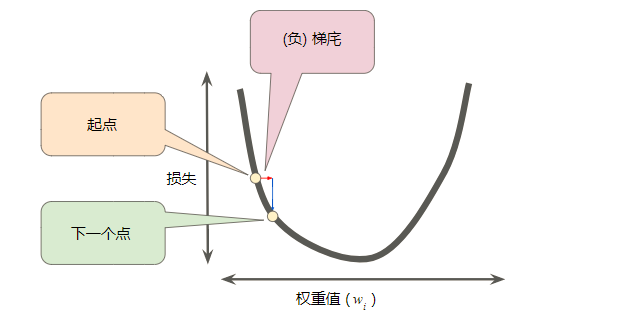
图 5. 一个梯度步长将我们移动到损失曲线上的下一个点。
然后,梯度下降法会重复此过程,逐渐接近最低点。