字符串匹配算法(暴力匹配与kmp算法)
1.暴力匹配算法
顾名思义,暴力匹配算法就是用for循环暴力匹配,将两个字符串逐一匹配,一直匹配到两个字符串相等或者直至字符串匹配结束,其时间复杂度为O(mn),其基本模板为:
int ViolentMatch(string s1,string s2)
{
int len1 = s1.size();
int len2 = s2.size();
int i = 0,j = 0,temp;
while (i < len1 && j < len2)
{
temp=i;
if (s[i] == p[j]) //匹配成功
{
i++;
j++;
}
else
{
i=temp+1
j = 0;
}
}
if (j == len2) //如果匹配成功
return i - j;
else
return -1;
}
其完整代码如下:
#include<iostream>
#include<string>
using namespace std;
int Violetmatch(string s1, string s2)
{
int len1, len2, temp;
len1 = s1.size();
len2 = s2.size();
int i = 0, j = 0;
while (i < len1&&j < len2)
{
temp = i;
if (s1[i] == s2[j])
{
i++;
j++;
}
else
{
i = temp + 1;
j = 0;
}
}
if (j == len2)
return i - j;
else
return -1;
}
int main()
{
string s1, s2;
cin >> s1 >> s2;
int ans;
ans=Violetmatch(s1, s2);
if (-1 == ans)
cout << "not find" << endl;
else
cout << "Match successfully in the " << ans+1 <<"-th of s1"<< endl;
return 0;
}
2.kmp算法
先上完整代码:
#include<iostream>
using namespace std;
const int N = 100005;
char s[N], p[N]; //s为主串,p为模式子串
int nnest[N]; //nest数组
void getnnest(char *p);
int kmp(char *s, char *p);
int main()
{
cin >> s >> p;
cout << kmp(s, p) << endl;
return 0;
}
void getnnest(char *p)
{
int j = 0, k = -1;
nnest[0] = -1;
int len = strlen(p);
while (j < len)
{
if (-1 == k || p[j] == p[k])
{
j++;
k++;
nnest[j] = k;
}
else
k = nnest[k];
}
}
int kmp(char *s, char *p)
{
getnnest(p);
int lens = strlen(s);
int lenp = strlen(p);
int k = 0;
for (int i = 0; i < lens; i++)
{
while (k&&s[i] != p[k])
k = nnest[k];
if (s[i] == p[k])
k++;
if (k == lenp)
return i - lenp + 1;
}
return -1;
}
注意不要使用string类型,因为string类型的字符串比char数组耗时,比赛时容易超时!
参考来源:CSDN的一位大佬的博客:https://blog.csdn.net/v_july_v/article/details/7041827
这里是匹配过程的详解
kmp用来处理长字符串或则数据量非常大的字符串时非常实用,因其时间复杂度只有O(m+n),其算法流程如下:
假设现在文本串S匹配到 i 位置,模式串P匹配到 j 位置
如果j = -1,或者当前字符匹配成功(即S[i] == P[j]),都令i++,j++,继续匹配下一个字符;
如果j != -1,且当前字符匹配失败(即S[i] != P[j]),则令 i 不变,j = next[j]。此举意味着失配时,模式串P相对于文本串S向右移动了j - next [j] 位。
换言之,当匹配失败时,模式串向右移动的位数为:失配字符所在位置 - 失配字符对应的next值,即移动的实际位数为:j - next[j],且此值大于等于1。
故问题转化为如何求next数组,next数组可以通过两个方式求得:
1.若要求next[j]的值,我们只需知道next数组的前面的值,再通过运算求得;
2.我们还可以根据前面j-1个字符串的最长前缀后缀,再讲所求的的各个最长前缀后缀的值向后移一位,再讲next[0]=-1赋初值,即可快速求得各个next数组的值。
寻找最长前缀后缀即相应next数组的值
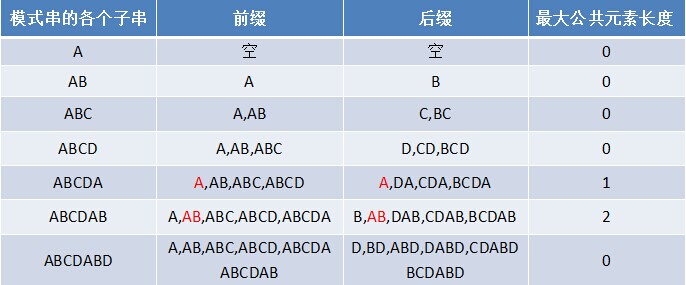
如果给定的模式串是:“ABCDABD”,从左至右遍历整个模式串,其各个子串的前缀后缀分别如下表格所示:
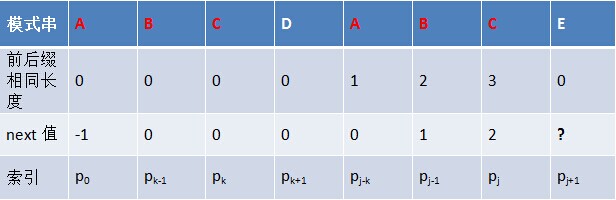
所以我们可以将最长前缀后缀的各个值向后移一位,再讲初值赋为-1,即可得到next数组,例如若对于给定的模式串:ABCDABD,它的最大前缀后缀长度表及next数组分别如下:
接下来我们就可以根据next数组求出模式字符串向右移动的位置,即
模式串向右移动的位数 = 失配字符所在的位置 - 失配字符对应的next值
或者说根据最大前缀后缀的长度值来说
模式串向右移动的位数 = 已经匹配的字符数 - 失配字符的上一位字符的最大前缀后缀长度值
通过代码递推计算next数组
1.如果对于值k,已有p0 p1 ... pk-1 = pj-k pj-k+1, ..., pj-1,相当于next[j]=k;其原因是这里相当于p[j]之前的模式串子串中,有长度为k的相同前缀和后缀;
2.下面的问题是:已知next[0, ..., j],如何求出next[j + 1]呢?这里有这么几个规律:
若p[k] == p[j],则next[j+1]=next[j]+1=k+1;
若p[k]≠p[j],如果此时p[next[k]]==p[j],则next[j+1]=next[k]+1,否则继续递归前缀索引k=next[k],而后重复此过程。 相当于在字符p[j+1]之前不存在长度为k+1的前缀"p0 p1, …, pk-1 pk"跟后缀“pj-k pj-k+1, …, pj-1 pj"相等,那么是否可能存在另一个值t+1 < k+1,使得长度更小的前缀 “p0 p1, …, pt-1 pt” 等于长度更小的后缀 “pj-t pj-t+1, …, pj-1 pj” 呢?如果存在,那么这个t+1 便是next[ j+1]的值,此相当于利用已经求得的next 数组(next [0, ..., k, ..., j])进行P串前缀跟P串后缀的匹配。
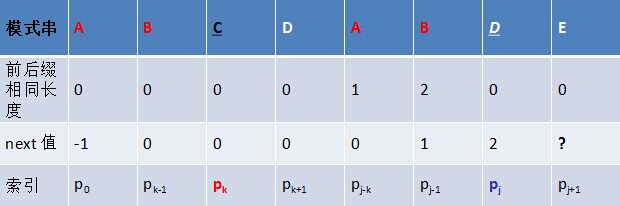
如下图所示,假定给定模式串ABCDABCE,且已知next [j]=k(相当于“p0 pk-1” = “pj-k pj-1” = AB,可以看出k为2),现要求next[j+1]等于多少?因为pk =pj=C,所以next[j+1] = next[j]+1=k+1(可以看出next[j+1]=3)。代表字符E前的模式串中,有长度k+1 的相同前缀后缀。
但如果pk != pj 呢?说明“p0 pk-1 pk” ≠ “pj-k pj-1 pj”。换言之,当pk != pj后,字符E前有多大长度的相同前缀后缀呢?很明显,因为C不同于D,所以ABC跟ABD不相同,即字符E前的模式串没有长度为k+1的相同前缀后缀,也就不能再简单的令:next[j+1]=next[j]+1 。所以,咱们只能去寻找长度更短一点的相同前缀后缀
结合上图来讲,若能在前缀“ p0 pk-1 pk ” 中不断的递归前缀索引k=next [k],找到一个字符pk’ 也为D,代表pk’=pj,且满足p0 pk'-1 pk' = pj-k' pj-1 pj,则最大相同的前缀后缀长度为k'+1,从而next[j+1]=k’+1=next[k']+1。否则前缀中没有D,则代表没有相同的前缀后缀,next[j+1]=0。
但是这样还有一个问题,比如字符串abab,p[3]=b,s[3]=c失配p[next[3]]=p[1]=b再跟s[3]匹配时,必然失配,所以我们需要改进一下算法避免这种情况发生,即不允许p[j]=p[next[j]];
综上,我们可以通过递推求得next数组,其代码如下所示:
void GetNext(string s1,int next[])
{
int len=s1.size();
next[0]=-1;
int k=-1;
int j=0;
while(j<len)
{
//p[k]表示前缀,p[j]表示后缀
if (k == -1 || p[j] == p[k])
{
++k;
++j;
if(p[j]!=p[k])
next[j] = k; //为了防止重复
else
next[j]=next[k];
}
else
{
k = next[k];
}
}
}