数据结构与算法(一)（数组、线性查找、二分查找）

 根据B站视频做的笔记及一些个人理解

https://www.bilibili.com/video/av33835237

 

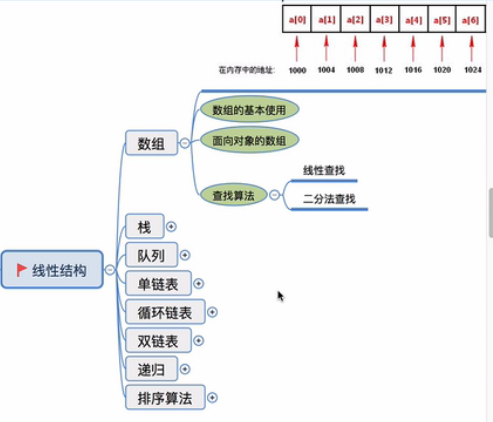
一、数组(有索引下标，所以查找快，增删慢)

 

　　1.1数组元素的基本使用

　　

结果：

 

public static void main(String[] args) {
        //创建一个数组
        int[] arr = new int[3];
        //获取数组长度
        int length1 = arr.length;
        System.out.println("数组的长度为:"+length1);
        //访问数组中的元素:数组名[下标],注意:下标从0开始，最大到数组长度-1,如果大于这个长度会抛异常
        int element0 = arr[0];
        System.out.println("element0"+":"+element0);
        //为数组中的元素赋值
        arr[0] = 99;
        System.out.println("element0"+":"+arr[0]);
        arr[1] = 98;
        arr[2] = 97;
        //遍历数组
        for(int i = 0 ; i < arr.length ; i++){
            System.out.println("arr element"+i+":"+arr[i]);
            
        }
        //创建数组的同时给数组赋值
        int[] arr1 = new int[]{10,2,0,30,40};
        //获取数组长度
        System.out.println("arr1 length"+arr1.length);
    }

 　　1.2数组元素的增加

　　　　其实也就是解决数组长度不可变的问题

　　　　思路：我们可以创建一个新的数组，然后新的数组长度为原数组的长度+1，在放入原数组的元素，替换原数组

　　　　

　　　　结果

　　　　

　　　　

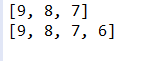
public static void main(String[] args) {
        //解决数组长度不可变的问题
        //创建数组
        int[] arr = new int[]{9,8,7};
        //快速查看数组中的元素
        System.out.println(Arrays.toString(arr));
        //要加入数组的目标元素
        int dst=6;
        
        //创建一个新的数组,长度是原数组长度+1
        int[] newArr = new int[arr.length+1];
        //把原数组中的数据全部复制到新数组中
        for(int i = 0 ; i < arr.length;i++){
            newArr[i] = arr[i];
        }
        //把目标元素放入新数组的最后
        newArr[arr.length] = dst;
        //新数组替换原数组
        arr = newArr;
        System.out.println(Arrays.toString(newArr));
    }

　　1.3数组元素的删除

 　　思路：我们可以创建一个新的数组，然后新的数组长度为原数组的长度-1，复制原数组中除了要删除的那个元素以外其他的元素

　　

　　结果　　

　　

　　

　　

public class arrayTest3 {
    //如何删除数组中的元素
    public static void main(String[] args) {
        //创建数组
        int[] arr = new int[]{9,8,7,6,5,4};
        System.out.println(Arrays.toString(arr));
        //要删除的元素下标
        int dst = 3;
        
        //创建一个新的数组,长度是原数组的长度-1
        int[] newArr = new int[arr.length-1];
        //复制原数组中除了要删除的那个元素以外其他的元素
        for(int i=0;i<newArr.length;i++){
            //要删除的元素之前的元素(直接对应赋值)
            if(i<dst){
                newArr[i]=arr[i];
            //要删除的元素之后的元素
            }else{
                newArr[i]=arr[i+1];
            }
        }
        //新数组替换旧数组
        arr = newArr;
        System.out.println(Arrays.toString(arr));
    }
}

 　　1.4面向对象的数组(我个人理解就是动态数组)

　　　　感觉就是写一个简略版的ArrayList，可以帮助我们理解ArrayList的源码

　　　　首先写一个工具类，封装数组及方法

　　　　

　　　　

　　　　

　　　　

　　　　

　　　　

　　　　

　　　　

    // 用于存储数据的数组
    private int[] elements;

    public MyArray() {
        elements = new int[0];
    }

    // 获取数组长度的方法
    public int size() {
        return elements.length;
    }

    // 往数组的末尾添加一个元素
    public void add(int element) {
        // 创建一个新的数组
        int[] newArr = new int[elements.length + 1];
        // 把原数据复制到新数组中
        for (int i = 0; i < elements.length; i++) {
            newArr[i] = elements[i];
        }
        // 把添加的元素放入新数组中
        newArr[elements.length] = element;
        // 使用新数组替换久数组
        elements = newArr;

    }

    // 打印所有元素到控制台
    public void show() {
        System.out.println(Arrays.toString(elements));
    }

    // 删除数组中的元素
    public void delete(int index) {
        // 判断下标是否越界
        if (index < 0 || index > elements.length - 1) {
            throw new RuntimeException("下标越界");
        }
        // 创建一个新数组,长度为原数组长度-1
        int[] newArr = new int[elements.length - 1];
        // 复制原有元素到新数组
        for (int i = 0; i < newArr.length; i++) {
            // 想要删除的元素前面的元素
            if (i < index) {
                newArr[i] = elements[i];
                // 想要删除的元素后面的元素
            } else {
                newArr[i] = elements[i + 1];
            }
        }
        // 新数组替换老数组
        elements = newArr;

    }

    // 获取指定位置的元素
    public int get(int index) {
        return elements[index];
    }

    // 插入一个元素到指定位置
    public void insert(int index, int element) {
        // 创建一个新的数组
        int[] newArr = new int[elements.length + 1];
        // 将原数组中的元素放入新数组
        for (int i = 0; i < elements.length; i++) {
            // 目标位置之前的元素
            if (i < index) {
                newArr[i] = elements[i];
                // 目标位置之后的元素
            } else {
                newArr[i + 1] = elements[i];
            }
        }
        // 插入新的元素
        newArr[index] = element;
        elements = newArr;
    }

    // 替换指定位置的元素
    public void set(int index, int element) {
        // 判断下标是否越界
        if (index < 0 || index > elements.length - 1) {
            throw new RuntimeException("下标越界");
        }
        elements[index] = element;
    }

测试类

　　

    public static void main(String[] args) {
        //创建一个动态数组
        MyArray ma = new MyArray();
        //获取长度
        int size = ma.size();
        System.out.println("长度为"+size);
        //往可变数组中添加一个元素
        ma.add(99);
        ma.add(98);
        ma.add(97);
        System.out.println(ma.size());
        ma.show();
        //删除元素
        ma.delete(1);
        ma.show();
        System.out.println(ma.size());
        //插入指定位置元素
        System.out.println(ma.get(0));
        System.out.println("---------------------------------");
        ma.add(96);
        ma.add(95);
        ma.add(94);
        ma.show();
        ma.insert(3, 3);
        ma.show();
        //替换指定位置元素
        ma.set(3, 4);
        ma.show();
        
        
    }

　　结果：

 　　1.6查找算法

　　　　　　1.6.1线性查找(效率低，如果特别多数据不建议)　

　　　　　　　　定义：

　　　　　　　　　　　　在一列给定的值中进行搜索，从一端开始逐一检查每个元素，直到找到所需元素的过程。

　　　　　　　　　　　　线性查找又称为顺序查找·

　　　　　　　　　　　　如果查找池是某种类型的一个表，比如一个数组，简单的查找方法是从表头开始，一次将每一个值与目标元素进行比较，最后，或者查找到目标，或者达到表尾，而目标不存在于组中，这个方法称为线性查找。

　　　　　　　　我们这里使用数组来学习线性查找，遍历数组，将目标值与数组值从头开始对比，当值相同，退出循环，打印下标，若查找不到，下标值为-1

　　　　　　　　

　　　　　　　　

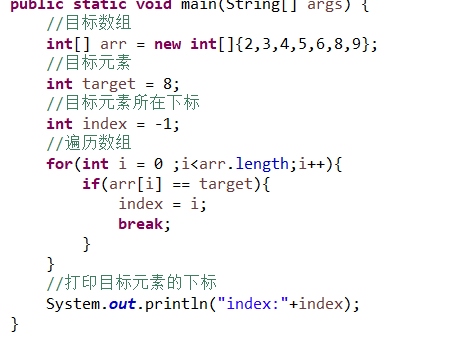
//目标数组
        int[] arr = new int[]{2,3,4,5,6,8,9};
        //目标元素
        int target = 8;
        //目标元素所在下标
        int index = -1;
        //遍历数组
        for(int i = 0 ;i<arr.length;i++){
            if(arr[i] == target){
                index = i;
                break;
            }
        }
        //打印目标元素的下标
        System.out.println("index:"+index);

　　　　　　结果：

　　　　　　　　　　

 

　　　　　　　　　　

　　　　　　1.6.2二分查找

　　　　　　　　　　定义：二分查找又称折半查找，优点是比较次数少，查找速度快，平均性能好，占用系统内存较少;其缺点是要求待查表为有序表，且插入删除困难。

　　　　　　　　　　　　　因此，折半查找方法适用于不经常变动而查找频繁的有序列表。

　　　　　　　　　　　　   首先，假设表中元素是按升序排列，将表中间位置记录的关键字与查找关键字比较，如果两者相等，则查找成功;

　　　　　　　　　　　　　否则利用中间位置记录将表分成前、后两个子表，如果中间位置记录的关键字大于查找关键字，则进一步查找前一子表，否则进一步查找后一子表。

　　　　　　　　　　　　　重复以上过程，直到找到满足条件的记录，使查找成功，或直到子表不存在为止，此时查找不成功。

　　　　　　　　　　　因为是需要有序的数组才能使用二分查找，我们可以定义一个begin和end还有mid，通过目标值比较中间值，对比大小，来移动begin或end到之前mid的位置，从而得到目标值的位置

　　　　　　

　　　　　　while()中的条件本来是true,但是这样如果目标值不在数组中，会导致死循环(因为走不到break那里。)

　　　　　　我们改成while(begin<=end)这样的话，如果的话，当程序走到最后剩中间两个数，再走下去begin就大于end了，程序终止

　　　　　　结果：

　　　　　　　　

 

　　　　      

public static void main(String[] args) {
        //目标数组
        int[] arr = new int[]{1,2,3,4,5,6,7,8,9};
        //目标元素
        int target = 8;
        //记录开始位置
        int begin = 0;
        //记录结束位置
        int end = arr.length-1;
        //记录中间位置
        int mid = (begin+end)/2;
        //记录目标位置
        int index = -1;
        while (begin<=end) {
            //判断中间这个元素是不是要找的元素
            if(arr[mid] == target){
                index = mid;
                break;
            //中间这个元素不是要查的元素
            }else {
                //判断中间这个元素是不是比目标元素要大
                if(arr[mid]>target){
                    //把结束位置调整到中间位置前一个位置
                    end = mid-1;
                //中间这个元素比目标元素小
                }else{
                    //把开始位置调整到中间位置的后一个位置
                    begin = mid+1;
                }
                //取出新的中间位置
                mid = (begin + end)/2;
            }
            
        }
        System.out.println("index:"+index);
    }

　　　　　　1.6.3整合查找算法

　　　　　　　　　　将线性查找和二分查找整合到我们的动态数组工具类里

　　　　　　　　　

//线性查找
    public int search(int target){
        // 遍历数组
        for (int i = 0; i < elements.length; i++) {
            if (elements[i] == target) {
                return i;
            }
        }
        return -1;
    }
    
    //二分法查找
    public int binarySearch(int target){
        // 记录开始位置
        int begin = 0;
        // 记录结束位置
        int end = elements.length - 1;
        // 记录中间位置
        int mid = (begin + end) / 2;
        // 记录目标位置
        int index = -1;
        while (begin <= end) {
            // 判断中间这个元素是不是要找的元素
            if (elements[mid] == target) {
                return mid;
                // 中间这个元素不是要查的元素
            } else {
                // 判断中间这个元素是不是比目标元素要大
                if (elements[mid] > target) {
                    // 把结束位置调整到中间位置前一个位置
                    end = mid - 1;
                    // 中间这个元素比目标元素小
                } else {
                    // 把开始位置调整到中间位置的后一个位置
                    begin = mid + 1;
                }
                // 取出新的中间位置
                mid = (begin + end) / 2;
            }

        }
        return index;
        
    }

 

 测试类：

　　　　

public static void main(String[] args) {
        MyArray ma = new MyArray();
        ma.add(1);
        ma.add(2);
        ma.add(3);
        ma.add(4);
        ma.add(5);
        //调用线性查找方法
        int index = ma.search(4);
        System.out.println(index);
        //调用二分法查找
        int index1 = ma.binarySearch(5);
        System.out.println(index1);
    }