冒泡排序
冒泡排序(英语:Bubble Sort)是一种简单的排序算法。它重复地遍历要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。遍历数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
冒泡排序算法的运作如下:
- 比较相邻的元素。如果第一个比第二个大(升序),就交换他们两个。
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
- 针对所有的元素重复以上的步骤,除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
时间复杂度
- 最优时间复杂度:O(n) (表示遍历一次发现没有任何可以交换的元素,排序结束。)
- 最坏时间复杂度:O(n2)
- 稳定性:稳定
冒泡排序的演示
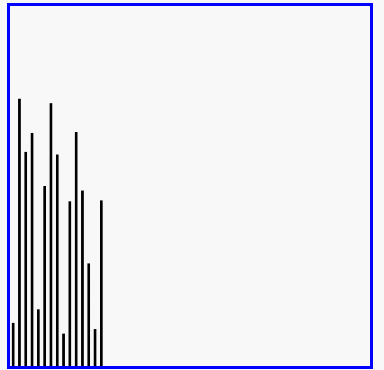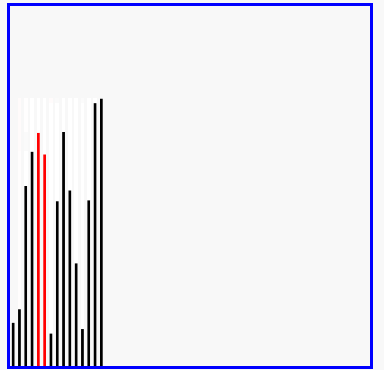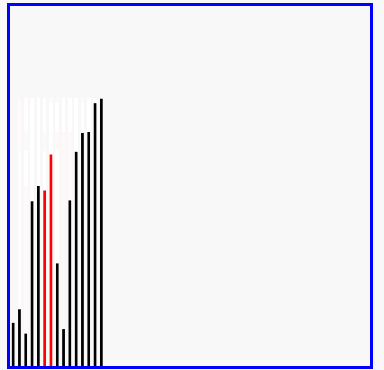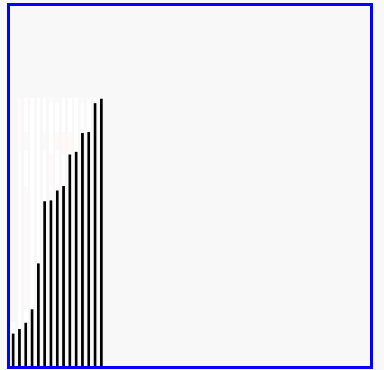
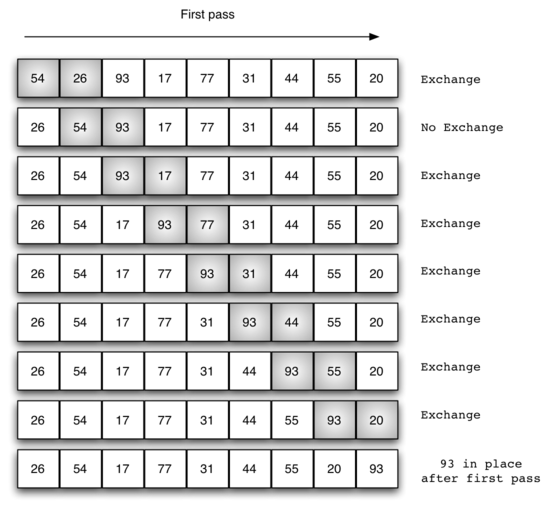
代码实现:
public class Main { public static void main(String[] args) { // TODO 自动生成的方法存根 int[] a = new int[] { 3, 6, 1, 2, 4, 5, 8, 7, 9, 0 }; boolean flag = true; int temp; for (int i = 1; i < a.length && flag; i++) { flag = false; for (int j = 1; j <= a.length - i; j++) { if (a[j - 1] > a[j]) { temp = a[j]; a[j] = a[j - 1]; a[j - 1] = temp; flag = true; } } } for (int x : a) { System.out.print(x + " "); } } }
选择排序
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理如下:
首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
选择排序的主要优点与数据移动有关。如果某个元素位于正确的最终位置上,则它不会被移动。选择排序每次交换一对元素,它们当中至少有一个将被移到其最终位置上,因此对n个元素的表进行排序总共进行至多n-1次交换。在所有的完全依靠交换去移动元素的排序方法中,选择排序属于非常好的一种。
时间复杂度
- 最优时间复杂度:O(n2)
- 最坏时间复杂度:O(n2)
- 稳定性:不稳定(考虑升序每次选择最大的情况)
选择排序演示
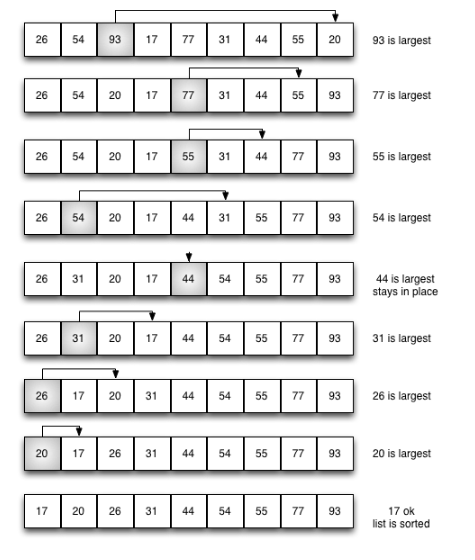
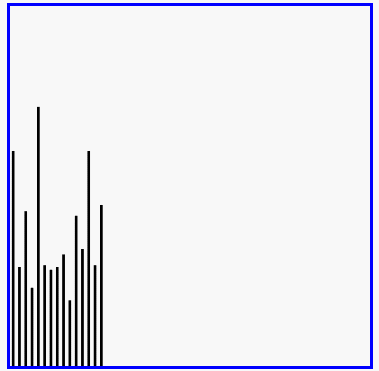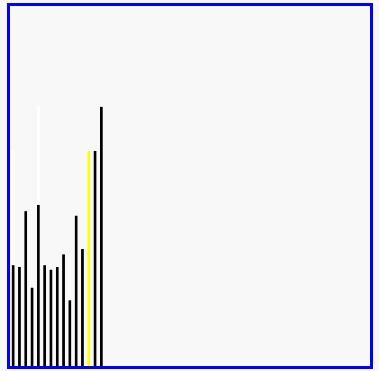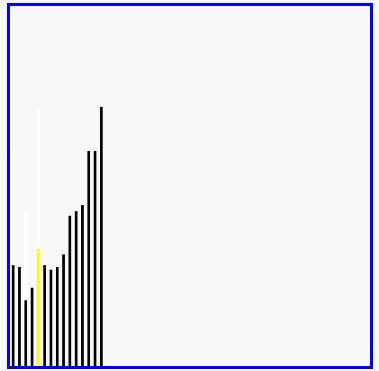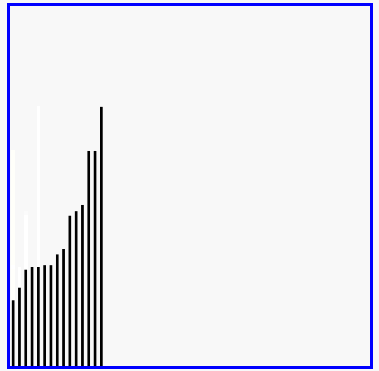
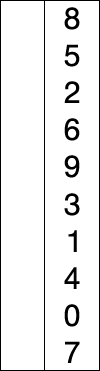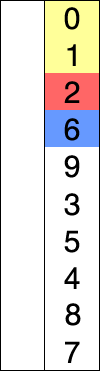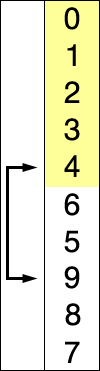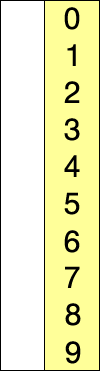
代码实现:
1 void select_sort(int *a,int n) 2 { 3 register int i,j,min,t; 4 for(i = 0;i < n-1;i++) 5 { 6 min = i;//查找最小值 7 for(j = i + 1;j < n;j++) 8 if(a[min] > a[j]) 9 min = j;//交换 10 if(min != i) 11 { 12 t = a[min]; 13 a[min] = a[i]; 14 a[i] = t; 15 } 16 } 17 }
插入排序
插入排序(英语:Insertion Sort)是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。
时间复杂度
- 最优时间复杂度:O(n) (升序排列,序列已经处于升序状态)
- 最坏时间复杂度:O(n2)
- 稳定性:稳定
插入排序演示
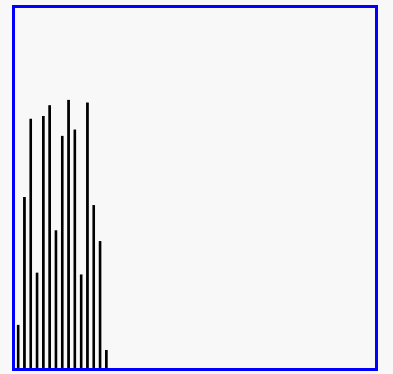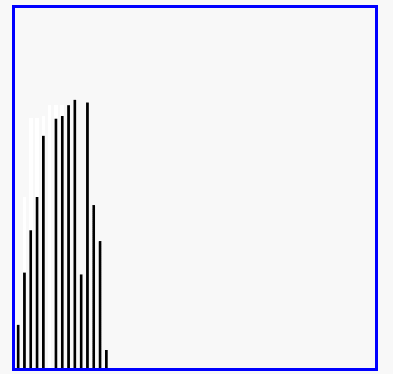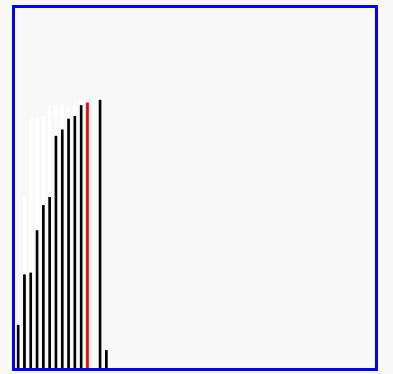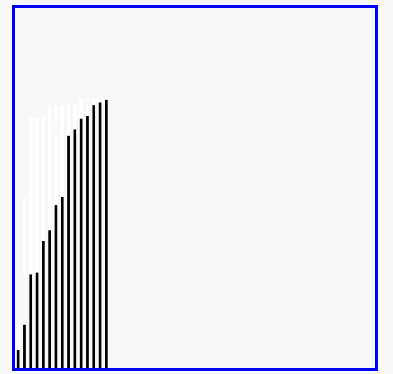
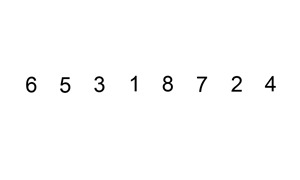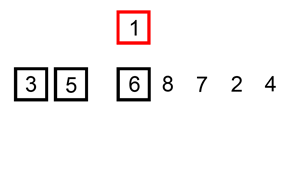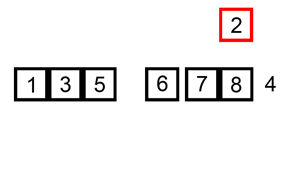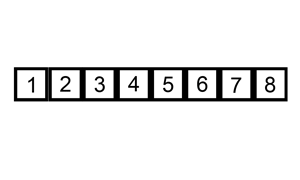
代码实现:
1 void insert_sort(int array[],unsignedint n) 2 { 3 int i,j; 4 int temp; 5 for(i = 1;i < n;i++) 6 { 7 temp = array[i]; 8 for(j = i;j > 0&& array[j - 1] > temp;j--) 9 { 10 array[j]= array[j - 1]; 11 } 12 array[j] = temp; 13 } 14 }
快速排序
快速排序(英语:Quicksort),又称划分交换排序(partition-exchange sort),通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
步骤为:
- 从数列中挑出一个元素,称为"基准"(pivot),
- 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区结束之后,该基准就处于数列的中间位置。这个称为分区(partition)操作。
- 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
递归的最底部情形,是数列的大小是零或一,也就是永远都已经被排序好了。虽然一直递归下去,但是这个算法总会结束,因为在每次的迭代(iteration)中,它至少会把一个元素摆到它最后的位置去。
时间复杂度
- 最优时间复杂度:O(nlogn)
- 最坏时间复杂度:O(n2)
- 稳定性:不稳定
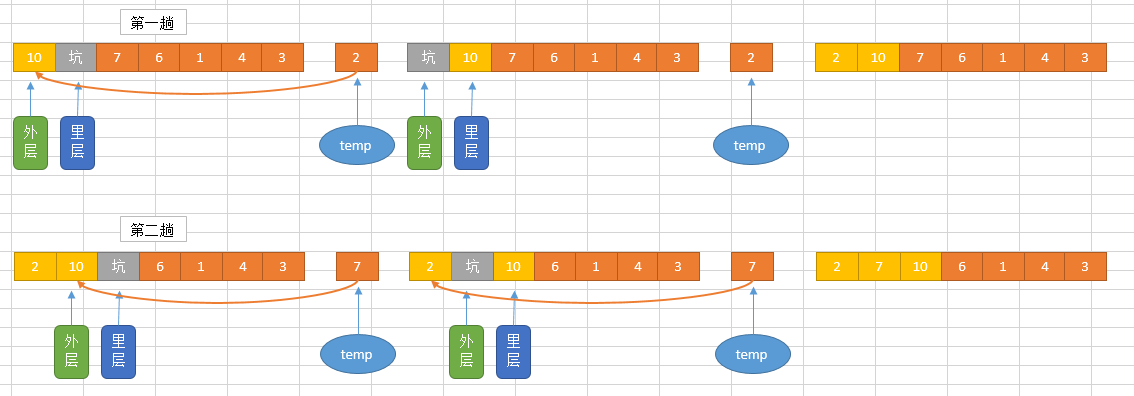
快速排序演示
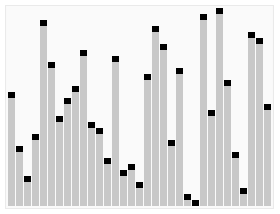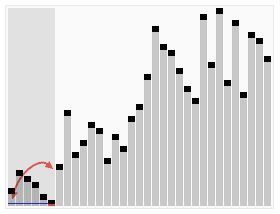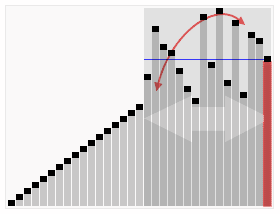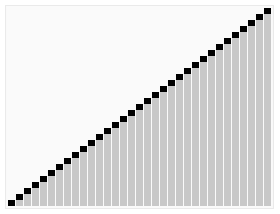

代码实现:
1 void Qsort(int a[], int low, int high) 2 { 3 if(low >= high) 4 { 5 return; 6 } 7 int first = low; 8 int last = high; 9 int key = a[first];/*用字表的第一个记录作为枢轴*/ 10 11 while(first < last) 12 { 13 while(first < last && a[last] >= key) 14 { 15 --last; 16 } 17 18 a[first] = a[last];/*将比第一个小的移到低端*/ 19 20 while(first < last && a[first] <= key) 21 { 22 ++first; 23 } 24 25 a[last] = a[first]; 26 /*将比第一个大的移到高端*/ 27 } 28 a[first] = key;/*枢轴记录到位*/ 29 Qsort(a, low, first-1); 30 Qsort(a, first+1, high); 31 }
希尔排序
希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序,是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因DL.Shell于1959年提出而得名。 希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。
希尔排序过程
希尔排序的基本思想是:将数组列在一个表中并对列分别进行插入排序,重复这过程,不过每次用更长的列(步长更长了,列数更少了)来进行。最后整个表就只有一列了。将数组转换至表是为了更好地理解这算法,算法本身还是使用数组进行排序。
希尔排序演示
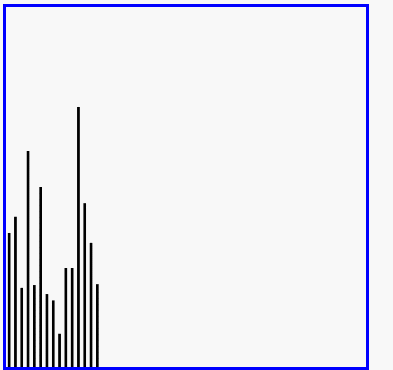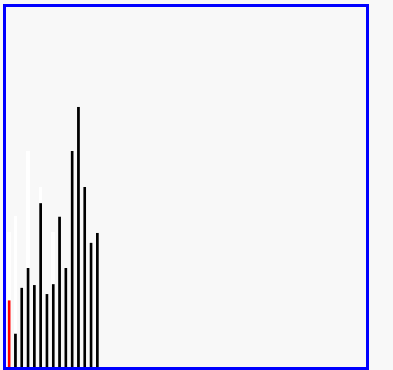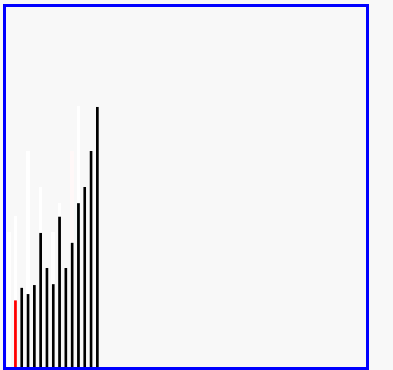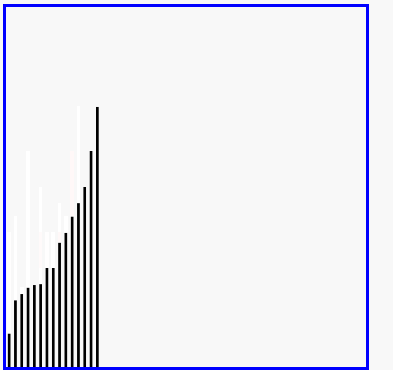
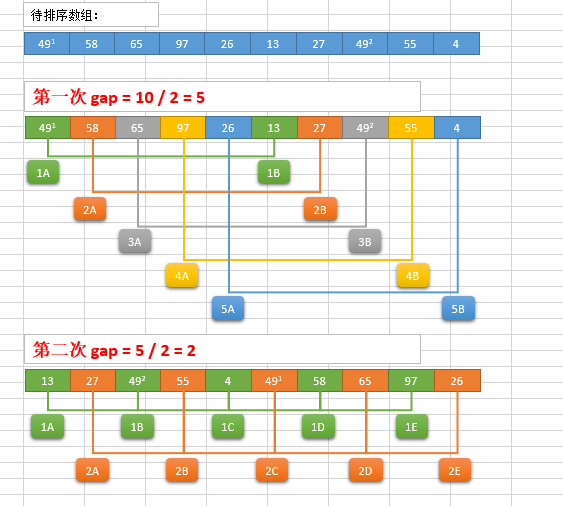
代码实现
1 #include<stdio.h> 2 #include<math.h> 3 4 #define MAXNUM 10 5 6 void main() 7 { 8 void shellSort(int array[],int n,int t);//t为排序趟数 9 int array[MAXNUM],i; 10 for(i = 0;i < MAXNUM;i++) 11 scanf("%d",&array[i]); 12 shellSort(array,MAXNUM,int(log(MAXNUM + 1) / log(2)));//排序趟数应为log2(n+1)的整数部分 13 for(i = 0;i < MAXNUM;i++) 14 printf("%d ",array[i]); 15 printf(" "); 16 } 17 18 //根据当前增量进行插入排序 19 void shellInsert(int array[],int n,int dk) 20 { 21 int i,j,temp; 22 for(i = dk;i < n;i++)//分别向每组的有序区域插入 23 { 24 temp = array[i]; 25 for(j = i-dk;(j >= i % dk) && array[j] > temp;j -= dk)//比较与记录后移同时进行 26 array[j + dk] = array[j]; 27 if(j != i - dk) 28 array[j + dk] = temp;//插入 29 } 30 } 31 32 //计算Hibbard增量 33 int dkHibbard(int t,int k) 34 { 35 return int(pow(2,t - k + 1) - 1); 36 } 37 38 //希尔排序 39 void shellSort(int array[],int n,int t) 40 { 41 void shellInsert(int array[],int n,int dk); 42 int i; 43 for(i = 1;i <= t;i++) 44 shellInsert(array,n,dkHibbard(t,i)); 45 } 46 47 //此写法便于理解,实际应用时应将上述三个函数写成一个函数。
归并排序
归并排序是采用分治法的一个非常典型的应用。归并排序的思想就是先递归分解数组,再合并数组。
将数组分解最小之后,然后合并两个有序数组,基本思路是比较两个数组的最前面的数,谁小就先取谁,取了后相应的指针就往后移一位。然后再比较,直至一个数组为空,最后把另一个数组的剩余部分复制过来即可。
归并排序的分析
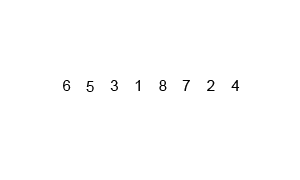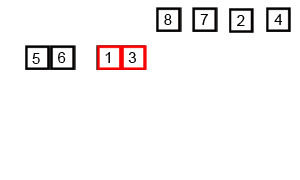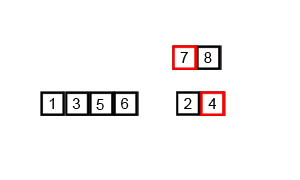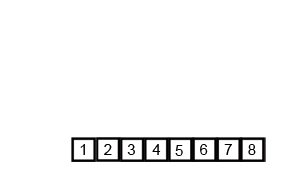
代码实现
1 #include <stdlib.h> 2 #include <stdio.h> 3 4 void Merge(int sourceArr[],int tempArr[], int startIndex, int midIndex, int endIndex) 5 { 6 int i = startIndex, j=midIndex+1, k = startIndex; 7 while(i != midIndex + 1 && j != endIndex + 1) 8 { 9 if(sourceArr[i] >= sourceArr[j]) 10 tempArr[k++] = sourceArr[j++]; 11 else 12 tempArr[k++] = sourceArr[i++]; 13 } 14 while(i != midIndex+1) 15 tempArr[k++] = sourceArr[i++]; 16 while(j != endIndex+1) 17 tempArr[k++] = sourceArr[j++]; 18 for(i = startIndex; i <= endIndex; i++) 19 sourceArr[i] = tempArr[i]; 20 } 21 22 //内部使用递归 23 void MergeSort(int sourceArr[], int tempArr[], int startIndex, int endIndex) 24 { 25 int midIndex; 26 if(startIndex < endIndex) 27 { 28 midIndex = (startIndex + endIndex) / 2; 29 MergeSort(sourceArr, tempArr, startIndex, midIndex); 30 MergeSort(sourceArr, tempArr, midIndex+1, endIndex); 31 Merge(sourceArr, tempArr, startIndex, midIndex, endIndex); 32 } 33 } 34 35 int main(int argc, char * argv[]) 36 { 37 int a[8] = {50, 10, 20, 30, 70, 40, 80, 60}; 38 int i, b[8]; 39 MergeSort(a, b, 0, 7); 40 for(i=0; i<8; i++) 41 printf("%d ", a[i]); 42 printf(" "); 43 return 0; 44 }
常见排序算法效率比较
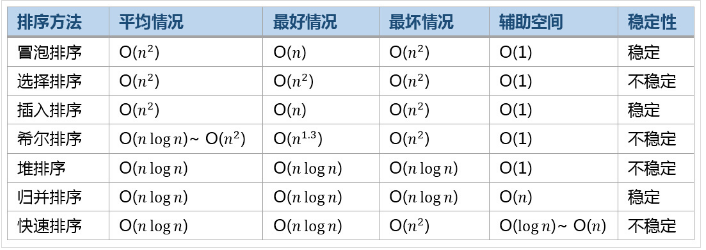
参考https://www.cnblogs.com/RainyBear/p/5258483.html