Codeforces1137D Cooperative Game

Description

Input

Output

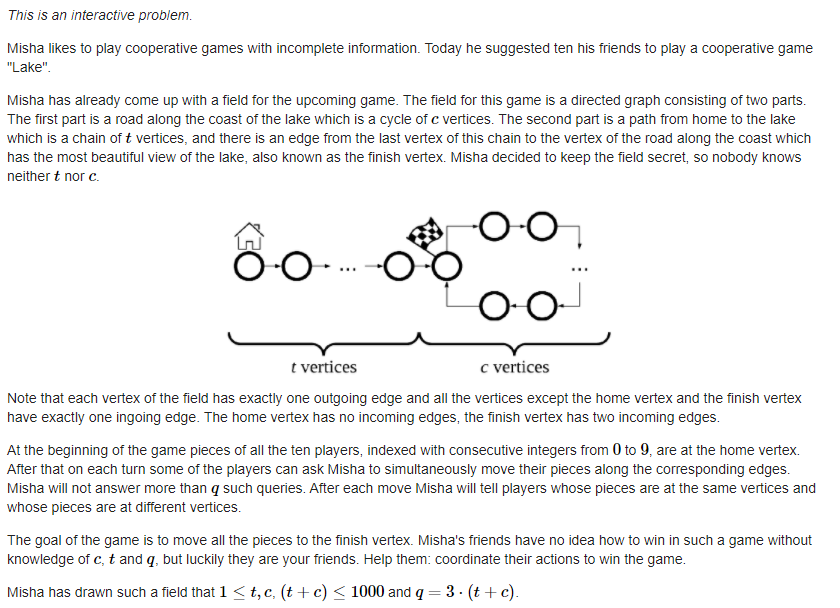
Solution

就是你有10个棋子,有一条边数为t的链和一个边数为c的环(t和c未知)组成的有向图,每次操作可以让一些棋子移动一步,让你在不超过(3 imes (t+c))次操作下让所有点移动到链和环连接的点处
首先我们考虑两个点动,剩下的点走t步走到终点
设0每两次操作走一次,1每次操作都走
当0走到连接处时,花费了2t步,还剩(t+3c)步
标记该点为0,然后按顺序给每个点按1~c-1标点
显然1的位置在(t%c)处
则1追上0需要2*(c-t%c)步
此时的位置应该是(c-t%c)
而再走t步的位置就回到了0
总步数(3t+(2c-t%c))<(3 imes (t+c))

#include <cstdio>
#include <algorithm>
#define open(x) freopen(x".in","r",stdin);freopen(x".out","w",stdout);
using namespace std;
char s[21];
int pd()
{
    int t;
    scanf("%d",&t);
    for (int i=1;i<=t;i++)
        scanf("%s",s);
    return t;
}
int main()
{
    open("cooperative");
    while (true)
    {
        printf("next 0 1
");
        fflush(stdout);
        pd();
        printf("next 1
");
        fflush(stdout);
        if (pd()==2) break;
    }
    while (true)
    {
        printf("next 0 1 2 3 4 5 6 7 8 9
");
        fflush(stdout);
        if (pd()==1) 
        {
            printf("done");
            fflush(stdout);
            exit(0);
        }
    }
    return 0;
}