先日常%foin
二叉搜索树(BST)
定义:要么是一棵空树,要么满足以下性质:
-
若左子树不为空,那么左子树中每一个节点所代表的数都比根节点所代表的数要小。
-
若右子树不为空,那么右子树中每一个节点所代表的数都比根节点所代表的数要大。
-
左、右子树均为二叉搜索树。
由于出题人很可能构造毒瘤数据,使 BST 退化为一条链,导致高度过高,所以需要通过伸展(splay)来优化运算速度。
怎么存
tot,表示 BST 中节点数量。
rt,表示 BST 中的根。
ch[n][2],其中ch[i][0]代表i号节点的左儿子,ch[i][1]代表i号节点的右儿子。
fa[N],其中fa[i]代表i号节点的父亲节点。
val[N],其中val[i]代表i号节点所存储的数。
sz[N],其中sz[i]代表以i号节点为根的子树的大小。
cnt[N],其中cnt[i]代表i号节点代表了几个数。由于可能会多次插入同一个数,所以需要记录每个数出现的次数。
操作
Splay 伸展树需要支持的基本操作有insert,delete,rank,kth,splay等。
辅助函数
which(i)函数代表节点i是fa[i]的左儿子还是右儿子。这个操作及其简单。
bool which(int x) {
return ch[fa[x]][1] == x;
}
pushup(i)函数表示更新以i节点为子树的大小。直接统计两颗子树相加再加上根节点的重数即可。
void pushup(int x) {
sz[x] = cnt[x] + sz[ch[x][0]] + sz[ch[x][1]];
}
伸展(Splay)
旋转 rotate
首先,需要旋转。rotate函数便是完成了旋转的工作。例如,最开始平衡树形态如下。
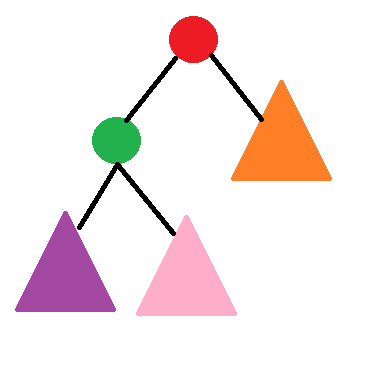
那么,可以将其做如下旋转。
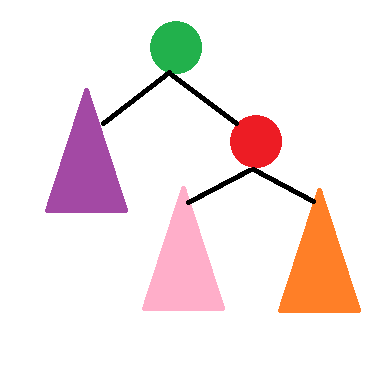
显然,旋转过后的BST仍然是满足BST的性质的,证明并不难。代码如下:
void rotate(int x) {
int y = fa[x], z = fa[y], k = chk(x), w = ch[x][k ^ 1];
ch[y][k] = w, fa[w] = y;
ch[z][chk(y)] = x, fa[x] = z;
ch[x][k ^ 1] = y, fa[y] = x;
pushup(y); pushup(x);
}
父节点会将连向需旋转的该子节点的方向的边连向该子节点位于其父节点方向的反方向的节点;然后爷爷节点会将连向父节点的边连向需旋转的该节点;最后需旋转的该节点会将连向该子节点位于其父节点方向的反方向的子节点的边连向其父节点。非人话但是自行模拟函数内容应该很容易理解。
伸展 splay
splay(i,goal)目的:将i通过rotate旋转到goal的儿子节点。实现方法:首先一个while循环,直到fa[x] = goal之前不停地找到其父亲以及其爷爷节点。注意:如果fa[fa[x]] = goal那么就直接旋转x就珂以了。而当x,fa[x],fa[fa[x]的which值都相同时,说明「三点一线」,那么要先旋转父节点。
void splay(int x, int goal = 0) {
while (fa[x] != goal) {
int y = fa[x], z = fa[y];
if (z != goal) {
if (which(x) == which(y)) rotate(y);
else rotate(x);
}
rotate(x);
}
if (!goal) {
root = x;
}
}
寻找 find
目的:将最大的小于等于的数 splay 到根。这个函数分两部分。首先
void find(int x) {
int cur = root;
while (ch[cur][x > val[cur]] && x != val[cur]) {
cur = ch[cur][x > val[cur]];
}
splay(cur);
}
交互操作
我也不知道为什么要取这个名字qwq.
反正大概就是跟用户交互的操作?
插入 insert
先放代码。
void insert(int x) {
int cur = root, p = 0;
while (cur && val[cur] != x) {
p = cur;
cur = ch[cur][x > val[cur]];
}
if (cur) {
cnt[cur]++;
} else {
cur = ++tot;
if (p) {
ch[p][x > val[p]] = cur;
}
val[cur] = x; fa[cur] = p;
cnt[cur] = sz[cur] = 1;
}
splay(cur);
}
首先,表示现在访问到的节点,而始终表示的父亲。接着一个while循环,如果要插入的数大于根,那么就到右儿子,否则到左儿子,直到不能继续为止。这时,如果现在 BST 中已经有,也就是指向的节点不为那么直接将其重数即可。否则,那么此时指向的节点编号为。说明 BST 中还没有这个数,那么就给数新建一个节点,编号为。那么此时就是的父亲节点。此时将ch[p][x>val[p]]赋值为tot即可。最后,对新建的节点进行初始化。这样,整个操作过程就完成了。
删除 remove
放代码。
void remove(int x) {
int last = pre(x), nxt = succ(x);
splay(last);
splay(nxt, last);
int del = ch[nxt][0];
if (cnt[del] > 1) {
cnt[del]--;
splay(del);
} else {
ch[nxt][0] = 0;
splay(nxt);
}
}
这个略微有一些复杂。首先,我们先不要管,pre和suf是什么last表示的是不大于于的最大的数。nxt表示的是不小于的最小的数。那么首先把splay到根,然后把splay到根的右儿子,那么此时由于右子树都大于,所以的左儿子一定大于,但是小于,所以一定是。这样,如果这个节点的重数,那么直接将重数即可。否则,如果这个节点重数,那么直接假删掉这个节点,将ch[nxt][0]设为,接着从一路splay到根更新一遍子树大小就可以了。
前驱 Precursor
int pre(int x) {
find(x);
if (val[root] < x) return root;
int cur = ch[root][0];
while (ch[cur][1]) {
cur = ch[cur][1];
}
return cur;
}
其实思路肥肠简单。首先把数旋转到根节点的位置。然后由于要找不大于于的最大的数,所以一定在左子树。所以将一个指针指向左子树的根节点,然后不停的走向右儿子,直到无法向右位置,此时这个指针就指向了的前驱。
后继 Successor
int succ(int x) {
find(x);
if (val[root] > x) {
return root;
}
int cur = ch[root][1];
while (ch[cur][0]) {
cur = ch[cur][0];
}
return cur;
}
其实思路根pre函数是完全一样的,就不加解释了。
第K大 K-th Number
int kth(int k) {
int cur = root;
while (1) {
if (ch[cur][0] && k <= sz[ch[cur][0]]) {
cur = ch[cur][0];
} else if (k > sz[ch[cur][0]] + cnt[cur]) {
k -= sz[ch[cur][0]] + cnt[cur];
cur = ch[cur][1];
} else {
return cur;
}
}
}
采用递归实现。从根节点开始,分类讨论:
-
ch[cur][0] && k <= sz[ch[cur][0]],也就是有左子树并且的大小。那么,这个数一定在左子树的第名。 -
k > sz[ch[cur][0]] + cnt[cur]也就是的大小比左子树的大小和根节点的重数之和都要大,说明一定是右子树的第k-(sz[ch[cur][0]] + cnt[cur])名。 -
否则,一定在根节点。
名次 Rank
int rank(int x) {
find(x);
return sz[ch[root][0]] + 1;
}
真的很简单。直接旋转到根节点,返回左子树的大小就可以了。
LOJ 104
注意有坑!!!!!
一定要插入两个哨兵0x3f3f3f3f和-0x3f3f3f3f,否则查到边界时会RE!!!
但是如果插入哨兵之后,rank函数要进行相应的改动,因为左子树已经多了一个节点,所以一定要改成
int rank(int x) {
find(x);
return sz[ch[root][0]];
}
直接上代码了。就是splay的模板题。