善意的投票:
因为只有(2)种意愿,不妨让想睡午觉的和源点连边,让不想睡午觉的和汇点连边。对于每一对好朋友,在他们之间连边。那么只要源点和汇点还联通,就存在一对好友是冲突的,我们现在要做的就是删去最少的边,使得源点和汇点孤立,问题转化为最小割,用最大流求解即可。
#include <bits/stdc++.h>
int n,m;
int S,T;
int head[200000],tot=1;
int cur[200000];
int deep[200000];
std::queue<int>q;
struct edge{
int to;
int nxt;
int flow;
}e[200000];
void add(int x,int y,int flow){
e[++tot]={y,head[x],flow};
head[x]=tot;
e[++tot]={x,head[y],0};
head[y]=tot;
}
bool bfs(){
memset(deep,0,sizeof deep);
deep[S]=1;
q.push(S);
while(!q.empty()){
int X=q.front();
q.pop();
for(int i=head[X];i;i=e[i].nxt){
int y=e[i].to;
if(!deep[y]&&e[i].flow){
deep[y]=deep[X]+1;
q.push(y);
}
}
}
return deep[T];
}
int dfs(int x,int flow){
if(x==T||!flow)
return flow;
int Flow=0;
for(int &i=cur[x];i;i=e[i].nxt){
int y=e[i].to;
if(e[i].flow&&deep[y]==deep[x]+1){
if(int w=dfs(y,std::min(flow,e[i].flow))){
e[i].flow-=w;
e[i^1].flow+=w;
Flow+=w;
flow-=w;
if(!flow)
break;
}
}
}
return Flow;
}
void dinic(){
int maxflow=0;
while(bfs()){
memcpy(cur,head,sizeof head);
while(int w=dfs(S,0x3f3f3f3f))
maxflow+=w;
}
printf("%d
",maxflow);
}
main(){
scanf("%d%d",&n,&m);
S=n+1;T=S+1;
for(int i=1,x;i<=n;++i){
scanf("%d",&x);
if(x)add(i,T,1);
else add(S,i,1);
}
for(int i=1,x,y;i<=m;++i){
scanf("%d%d",&x,&y);
add(x,y,1);
add(y,x,1);
}
dinic();
return 0;
}
再考虑小(M)的作物,按照之前的做法,对于每种作物,向源点和汇点分别连对应价值流量大小的边,考虑那些组合收益,假设我们需要获得那些作物在(A)中的收益,那么当组合中的所有点都和(B)断开后,我们才能保留这条边,所以我们可以这样连边:源点到这个点对应的点(x),流量为组合中的作物都种在(A)的价值,这个点向所有组合中的点连边,边权都为(infty)。组合中的作物都对这个点对应的点(x')连边,流量为(infty),(x')向汇点连边,流量为组合都种在(B)的价值。
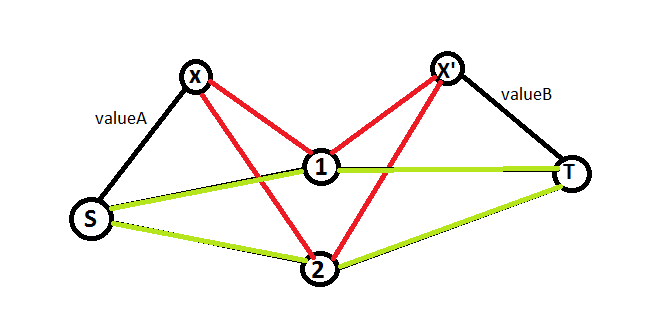
问题得解。
#include <bits/stdc++.h>
#define int long long
int n,kind,S=1,T=2;
int ans;
int head[1000001],tot=1;
int cur[1000000];
int deep[5001];
struct edge{
int to,nxt,flow;
}e[4000000];
std::queue<int>q;
void add(int x,int y,int flow){
e[++tot]={y,head[x],flow};
head[x]=tot;
e[++tot]={x,head[y],0};
head[y]=tot;
}
bool bfs(){
while(!q.empty())q.pop();
memset(deep,-1,sizeof deep);
deep[S]=0;
for(int i=0;i<=tot;++i)
cur[i]=head[i];
q.push(S);
while(!q.empty()){
int X=q.front();
q.pop();
for(int i=head[X],y;i;i=e[i].nxt){
y=e[i].to;
if(deep[y]<0&&e[i].flow){
deep[y]=deep[X]+1;
q.push(y);
if(y==T)
return 1;
}
}
}
return 0;
}
int dfs(int x,int flow){
if(x==T||!flow)
return flow;
int Flow=0;
for(int &i=cur[x],y;i;i=e[i].nxt){
y=e[i].to;
if(e[i].flow&&deep[y]==deep[x]+1){
if(int w=dfs(y,std::min(flow,e[i].flow))){
e[i].flow-=w;
e[i^1].flow+=w;
Flow+=w;
flow-=w;
if(!flow)break;
}
}
}
if(!flow)
deep[x]=-1;
return Flow;
}
void dinic(){
while(bfs())
ans-=dfs(S,1e9);
printf("%lld
",ans);
}
main(){
scanf("%lld",&n);
for(int i=1,x;i<=n;++i){
scanf("%lld",&x);
add(S,i+2,x);
ans+=x;
}
for(int i=1,x;i<=n;++i){
scanf("%lld",&x);
add(i+2,T,x);
ans+=x;
}
scanf("%d",&kind);
for(int i=1,th,valueA,valueB;i<=kind;++i){
scanf("%lld%lld%lld",&th,&valueA,&valueB);
ans+=valueA+valueB;
add(S,n+2+i,valueA);
add(n+2+i+kind,T,valueB);
for(int j=1,x;j<=th;++j){
scanf("%lld",&x);
add(n+2+i,2+x,1e6);
add(2+x,n+2+i+kind,1e6);
}
}
dinic();
return 0;
}