蓝桥杯 方格分割
【题目描述 - Problem Description】
6x6的方格,沿着格子的边线剪开成两部分。
要求这两部分的形状完全相同。
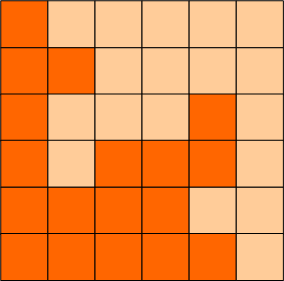
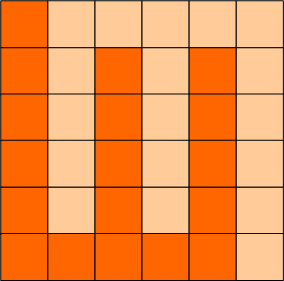

如图:p1.png, p2.png, p3.png 就是可行的分割法。
试计算: 包括这3种分法在内,一共有多少种不同的分割方法。
注意:旋转对称的属于同一种分割法。
请提交该整数,不要填写任何多余的内容或说明文字。
【题解】
DFS暴力枚举,和之前的剪邮票一个套路。由于需要考虑旋转对称造成的重复,最后结果除4。
多注意剪枝,可以让代码快很多。
【最终结果】
509
【代码 C++】
1 #include <cstdio> 2 struct Point { 3 int y, x; 4 }pit[36]; 5 int map[10][10], stk[18], opt; 6 int sum(int y, int x) { 7 if (map[y][x] == 1) { 8 map[y][x] = 2; 9 return 1 + sum(y + 1, x) + sum(y - 1, x) + sum(y, x + 1) + sum(y, x - 1); 10 } 11 return 0; 12 } 13 void DFS(int now, int i) { 14 if (i < 18) { 15 while (++now < 19 + i) { 16 if (map[7 - pit[now].y][7 - pit[now].x]) continue; 17 stk[i] = now; 18 map[pit[now].y][pit[now].x] = 1; 19 DFS(now, i + 1); 20 map[pit[now].y][pit[now].x] = 0; 21 } 22 } 23 else { 24 for (i = 0; i < 18; ++i) map[pit[stk[i]].y][pit[stk[i]].x] = 1; 25 if (sum(pit[stk[0]].y, pit[stk[0]].x) == 18) ++opt; 26 } 27 } 28 void init() { 29 int i, j, iPit = 0; 30 for (i = 1; i <= 6; ++i) for (j = 1; j <= 6; ++j) { 31 pit[iPit].y = i; pit[iPit].x = j; 32 ++iPit; 33 } 34 } 35 int main() { 36 init(); 37 DFS(-1, 0); 38 printf("%d", opt >> 2); 39 return 0; 40 }