FJNU 1153 Fat Brother And XOR(胖哥与异或)
Time Limit: 1000MS Memory Limit: 257792K
|
【Description】 |
【题目描述】 |
|
Fat brother had master ACM, recently he began to study the operation of XOR (the operation “^”). He thought of a very interesting question: select arbitrary k positive integers from the n positive integers, then XOR the selected k digital, sum all cases of XOR. Now he wants to quickly calculate the results. Maybe the results will be great, just modulo 20162333. For example, 3 integers: 1 2 3, select arbitrary 2 positive integers, the all cases: {1,2}, {2, 3}, {1, 3}. So the results is {(1 ^ 2) + (2 ^ 3) + (1 ^ 3)} %20162333 |
胖哥是个ACM大牛,最近他在学习异或操作(运算符为“^”)。他想到了个有趣的问题:从n个正整数中任选k个,然后对这k个数异或,对所有异或的结果求和。现在他想快速计算结果。最终结果可能很大,于是模20162333。 例如,3个整数:1 2 3,选择任意2个正整数,所有情况为: {1,2}, {2, 3}, {1, 3}。因此结果为{(1 ^ 2) + (2 ^ 3) + (1 ^ 3)} %20162333 |
|
【Input】 |
【输入】 |
|
There are multiple test cases. The first line of input contains an integer T (T <= 20) indicating the number of test cases. For each test case: The first line contains two integer n, k (1 <= k <= n <= 1000) The second line contains n integer ai (1 <= ai <= 1000000000) |
多组测试用例。 第一行是一个整数T(T <= 20)表示测试用例的数量。对于每个测试用例: 第一行有两个整数,k(1 <= k <= n <= 1000) 第二行有n个整数ai(1 <= ai <= 1000000000) |
|
【Output】 |
【输出】 |
|
For each test case, output the sum % 20162333 |
对于每个测试用例,输出和%20162333 |
|
【Sample Input - 输入样例】 |
【Sample Output - 输出样例】 |
|
2 3 2 1 2 3 6 2 6 6 6 6 6 6 |
6 0 |
|
【Hint】 |
【提示】 |
|
The first sample test case: (1 ^ 2) + (2 ^ 3) + (1 ^ 3) = 6 The second sample test case: (6 ^ 6) * 15 = 0 |
第一个样例: (1 ^ 2) + (2 ^ 3) + (1 ^ 3) = 6 第二个样例: (6 ^ 6) * 15 = 0 |
【题解】
这道题需要以二进制的观点来看待每个ai
举个例子:
Xai表示二进制的下ai的第X位(为方便表示从0开始)
(a1 ^ a2) + (a2 ^ a3) + (a1 ^ a3)
=[(0a1 ^ 0a2) + (0a2 ^ 0a3) + (0a1 ^ 0a3)]*20 +
[(1a1 ^ 1a2) + (1a2 ^ 1a3) + (1a1 ^ 1a3)]*21 +
[(2a1 ^ 2a2) + (2a2 ^ 2a3) + (2a1 ^ 2a3)]*22 +
…………………………………………………………………………… +
[(Xa1 ^ Xa2) + (Xa2 ^ Xa3) + (Xa1 ^ Xa3)]*2X
此时只剩0和1了
我们可以很轻易地知道:0 ^ 0 = 0, 1 ^ 0 = 1, 1 ^ 1 = 0
当然了,a ^ b = b ^ a
所以除了1 ^ 0之外,其他结果为0的情况都是无用的。
因此,题目转换为:求二进制下,1 ^ 0 这种情况出现的次数。
统计ai中二进制第X位出现几次1,保存到bit[x]
第X位提供的1 = 2X * 有效情况数
有效情况数就是由bit[X]个1与 n-bit[X]个0组合出来的
并且只有取奇数个1的时候,异或的结果才能为1(1 ^ 1 = 0)
由此可以得出
当前有效情况数: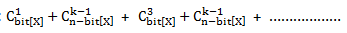
最后利用递推公式快速求组合数c(n,m)=c(n-1,m-1)+c(n-1,m)
(当然你把这个公式当成杨辉三角也是可以的:))
【代码 C++】
1 #include<cstdio> 2 #include <cstring> 3 #define mx 1005 4 #define mod 20162333 5 int main(){ 6 int t, n, k, i, j, w, opt, bit[30], c[mx][mx]; 7 for (i = 0; i < mx; ++i){ 8 for (c[i][0] = c[i][i] = j = 1; j < i; ++j) 9 c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod; 10 } 11 while (~scanf("%d", &t)){ 12 while (t--){ 13 memset(bit, 0, sizeof(bit)); 14 scanf("%d%d", &n, &k); 15 for (i = 0; i < n; ++i){ 16 scanf("%d", &j); 17 for (w = 0; j; j >>= 1) bit[w++] += j & 1; 18 } 19 for (i = opt = 0; i < 30; ++i){ 20 for (j = 1; j <= k; j += 2){ 21 opt += (1LL << i) *c[bit[i]][j] % mod*c[n - bit[i]][k - j] % mod; 22 opt %= mod; 23 } 24 } 25 printf("%d ", opt); 26 } 27 } 28 return 0; 29 }

1 #include<cstdio> 2 #include <cstring> 3 #define mx 1005 4 #define mod 20162333 5 int read_int(){ 6 int add = getchar() - '0'; 7 int a = getchar(); 8 while (a >= '0' && a <= '9') add = add * 10 + a - '0', a = getchar(); 9 return add; 10 } 11 int main(){ 12 int t, n, k, i, j, w, opt, bit[30], *c[mx]; 13 for (i = 0; i < mx; ++i){ 14 c[i] = new int[i + 1]; 15 for (c[i][0] = c[i][i] = j = 1; j < i; ++j) 16 c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod; 17 } 18 while (t = read_int(), t>0){ 19 while (t--){ 20 memset(bit, 0, sizeof(bit)); 21 n = read_int(); k = read_int(); 22 for (i = 0; i < n; ++i){ 23 for (w = 0, j = read_int(); j; j >>= 1) bit[w++] += j & 1; 24 } 25 for (i = opt = 0; i < 30; ++i){ 26 for (j = 1; j <= k; j += 2){ 27 if (bit[i] < j || n - bit[i] < k - j) continue; 28 opt += (1LL << i) *c[bit[i]][j] % mod*c[n - bit[i]][k - j] % mod; 29 opt %= mod; 30 } 31 } 32 printf("%d ", opt); 33 } 34 } 35 return 0; 36 }
