-
计算动态图像的梯度结构相似度(\(\mbox{NRSS}\)),数值低于一定阈值的图像被标记为模糊图像而被剔除;
-
结构相似度(\(\mbox{SSIM}\))
-
亮度比较(\(\mbox{lighting}\))
\[\mbox{l}(x,y)=\frac{2\mu_x\mu_y+C_1}{\mu_x^2+\mu_y^2+C_1} \] -
对比度比较(\(\mbox{contrast}\))
\[\mbox{c}(x,y)=\frac{2\sigma_x\sigma_y+C_2}{\sigma_x^2+\sigma_y^2+C_2} \] -
结构信息比较(\(\mbox{struct}\))
\[\mbox{s}(x,y)=\frac{\sigma_{xy}+C_3}{\sigma_x\sigma_y+C_3} \] -
结构相似度(\(\mbox{SSIM}\))
\[\mbox{SSIM}(x,y)=\mbox{l}^\alpha(x,y)\cdot\mbox{c}^\beta(x,y)\cdot\mbox{s}^\gamma(x,y) \] -
参数释义
\[\begin{aligned} &x&第一幅图像\\ &y&第二幅图像\\ &\mu_x,\mu_y&两幅图像各自平均值\\ &\sigma_x,\sigma_y&两幅图像各自方差\\ &\sigma_{xy}&两幅图像的协方差\\ &C_1,C_2,C_3&为了避免分母为0而设的常数\\ &\alpha,\beta,\gamma&代表不同特征的占比 \end{aligned} \]
-
-
无参考图像清晰度的评价指标(\(\mbox{NRSS}\))
-
构造参考图像\(I_r=\mbox{LPF}(I)\),即对图像\(I\)进行低通滤波处理(基于圆盘模型的均值滤波器和高斯模型的平滑滤波器也能有不错的效果),建议采用\(\mbox{size}=7\times7,\sigma^2=6\)的高斯平滑滤波器;
-
使用\(\mbox{Sobel}\)算子提取\(I,I_r\)的梯度图像(水平和垂直方向的边缘信息)分别记为\(G,G_r\);
-
将图像\(G,G_r\)按\(\mbox{size}=8\times8,\mbox{step=4}\)划分为若干图像块,方差越大表示梯度信息越丰富,找出其中方差最大的\(N\)块(建议值为64),\(G\)中的块记为\(\{x_i|i=1,\dots,N\}\)、\(G_r\)中的块记为\(\{y_i|i=1,\dots,N\}\);
-
利用结构相似度\(\mbox{SSIM}\)计算\(\mbox{NRSS}\):
\[\mbox{NRSS}=1-\frac{1}{N}\times{\sum_{i=1}^N{\mbox{SSIM}(x_i,y_i)}} \]
-
-
参考文献以及工具
-
-
自适应中值滤波去除椒盐噪声(中值滤波在去噪时容易平滑有效的边缘信息)
-
确定滤波器尺度:若\(Z_{\mbox{min}}\lt Z_{\mbox{mid}}\lt Z_{\mbox{max}}\),说明在\(S_{xy}\)中椒盐噪声含量不高(未过半),跳转\(\mbox{B}\)。否则增大滤波器尺度以适应高密度椒盐噪声(相当于稀释噪声密度),重复\(\mbox{A}\);
如果在重复执行\(\mbox{A}\)时滤波器尺度大于规定最大尺度,倘若椒盐噪声的密度依旧过大,则说明这幅图不适合用中值滤波的思想去噪,所以直接用该点的像素值\(Z_{xy}\)去替代\(Z_{\mbox{mid}}\),然后跳转\(\mbox{B}\)。
-
保留原始信息同时去噪:若\(Z_{\mbox{min}}\lt Z_{xy}\lt Z_{\mbox{max}}\),即该像素点不是最值(故不可能为椒盐噪声点),该点像素值保持不变。否则该点的像素值用\(Z_{\mbox{mid}}\)替代;
最糟糕的情况是滤波器尺度最大(\(Z_{\mbox{mid}}\)为椒盐噪声点)且该点(\(Z_{xy}\))为噪声点,不能去除掉,也就是说,对于图像中密度过大的区域,中值滤波的思想是不顶用的。
-
-
使用基于积分图像的自适应阈值化算法对滤波后图像进行二值化
-
积分图像
-
定义式
\[\mbox{I}(x,y)=\sum_{i=0,j=0}^{x,y}{f(x,y)} \] -
右下图可知\(\mbox{I}(x,y)=A+B+C+D+E+F+G+H+I\),按照递归的思想,观察其定义式可拆分组合为下式:
\[\begin{aligned} \mbox{I}(x,y)&=\scriptsize{(A+B+D+E+H+G)+(A+B+C+D+E+F)-(A+B+D+E)+I}\\ &=\mbox{I}(x-1,y)+\mbox{I}(x,y-1)-\mbox{I}(x-1,y-1)+f(x,y) \end{aligned} \]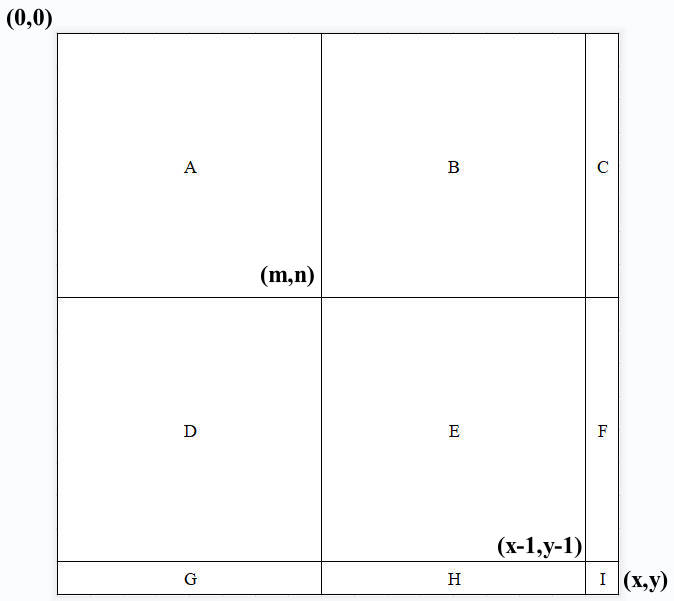
-
所以不难计算出任意点\((m,n)\)到\((x,y)\)的矩形围成的面积(积分图像)
\[\begin{aligned} \mbox{I}^{(x,y)}_{(m,n)}&=\mbox{I}(x,y)-\mbox{I}(m-1,y)-\mbox{I}(x,n-1)+\mbox{I}(m-1,n-1)\\ \mbox{I}^{(x_2,y_2)}_{(x_1,y_1)}&=\mbox{I}(x_2,y_2)-\mbox{I}(x_1-1,y_2)-\mbox{I}(x_2,y_1-1)+\mbox{I}(x_1-1,y_1-1) \end{aligned} \]
-
-
二值化
-
指定一个\(\mbox{size}=s,\mbox{center}=(x,y)\)的矩形滑动窗口\(W\),不难计算出\(W\)中的积分值
\[\mbox{I}_W=\mbox{I}(x_2,y_2)-\mbox{I}(x_1-1,y_2)-\mbox{I}(x_2,y_1-1)+\mbox{I}(x_1-1,y_1-1) \]其中\(x_1=x-\frac{s}{2}\),\(x_2=x+\frac{s}{2}\),\(y_1=y-\frac{s}{2}\),\(y_2=y+\frac{s}{2}\);
-
由此我们可以得出二值化图像
\[\mbox{BW}(x,y)= \begin{cases} 1&f(x,y)\ge T\\ 0&f(x,y)\lt T \end{cases} \quad\text{,} T=N\times\frac{I_W\times(100-t)}{100} \]其中\(t\)值需要实验对比得出较佳方案,\(N=(x_2-x_1)\times(y_2-y_1)\)。
-
-
-
对分割出来的矿石做外接矩形框,以便统计矿石的粒度分布;