写在前面
感谢 caq 的倾情讲解 
模拟退火是个随机化算法,正确性有一定保证,但如果你想我一样脸黑的话......
实测模拟退火做多了 rp 会掉
正文
简介
模拟退火是一种随机化算法,当一个问题的方案数量极大(甚至是无穷的)而且不是一个单峰函数时,我们常使用模拟退火求解。- Oi-wiki
什么是退火?
退火是一种金属热处理工艺,指的是将金属缓慢加热到一定温度,保持足够时间,然后以适宜速度冷却。目的是降低硬度,改善切削加工性;消除残余应力,稳定尺寸,减少变形与裂纹倾向;细化晶粒,调整组织,消除组织缺陷。准确的说,退火是一种对材料的热处理工艺,包括金属材料、非金属材料。而且新材料的退火目的也与传统金属退火存在异同。---百度百科
扯远了。
这个算法就是在温度不断降低的过程中,不断地从当前位置寻找别的位置进行计算,温度越低,也就是它的动能越小时,位置就会变化的越小,最后逐渐停留在最优解(或者附近)
算法流程
每次随机一个新的状态,如果状态更优就更新答案,否则以一定概率接受这个状态。
Metropolis准则
以求最小值为例。
-
如果 (Delta E < 0),说明当前解更优,直接更新即可
-
否则,如果
就接受这个状态。
- 否则 直接跳过。
为什么?
第一步因为是最优解所以一定选择更新答案
第二步后边的是一个随机值我们暂且不论。
考虑整个退火过程,
假设温度 (T) 不变,新的解越劣,(Delta E) 越大,左项的值越小,接受的概率也越小。
假设 (Delta E) 不变,随着温度的下降,求解的范围也趋于稳定,(T) 越小,左项得值也越小,接受的概率也越小
扔一张图可能会更好理解:
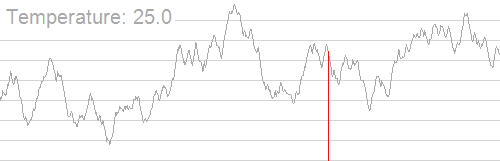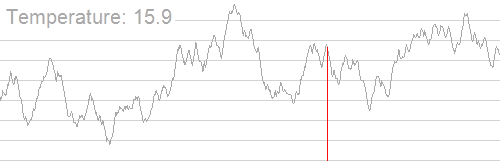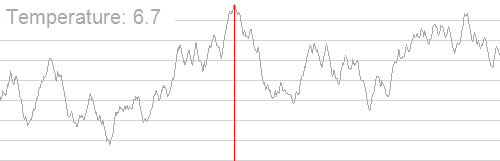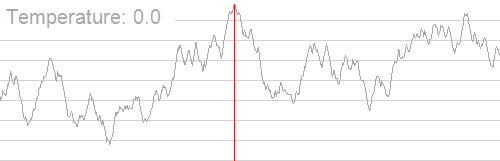
听上去很扯 ,但它还是有一定的正确性的。
SA 函数
通常降温系数 (d) 是一个很接近 (1) 的数,终止温度 (T_0) 是一个很接近 (0) 的数
这里给一个伪代码:
const double lim = ... // 温度最小值,通常为 1e-10 左右
const double d = ... // 变化系数,通常为 0.996 左右
void SA() {
double T = ... // 初始温度,通常为 2021 左右
while(T > lim) {
... // 获取一个随机的位置
now = calc(); // 计算当前位置的答案
del = now - ans; // 计算 变化量
if(del < 0) { // 以最小值为例
ans = now; // 更新答案
... // 更新答案和中间量的状态
} else if(exp(-del/T) > (double)rand()/RAND_MAX) {
... // 一定概率选择当前当前状态
}
T *= d; // 降温
}
}
计算函数 calc
依据题目而定,这里不给出
一些技巧/思想
如果想要随机一个无限大平面内的一个点,可以这样:
double nowx = limx + ((rand() << 1) - RAND_MAX) * T;
double nowy = limy + ((rand() << 1) - RAND_MAX) * T;
其中 nowx,nowy 是我们随机的位置, limx, limy 是我们一个中间状态的位置(注意不是答案的位置),
后面的那一坨刚好对应着温度越小变化越小的实际情况。
我们有时为了使得到的解更有质量,会在模拟退火结束后,以当前温度在得到的解附近多次随机状态,尝试得到更优的解(其过程与模拟退火相似)。
模拟退火是个随机的算法,执行次数越多获得的解越有可能更优,所以我们可以执行多遍 SA 函数。至于如何控制时间?
while((double)clock()/CLOCKS_PER_SEC < 0.90) SA();
上面这个代码控制时间在 (0.90s) 左右,如果时间限制为 (1s),而每次 SA 函数执行时间略长时,就要小心可能会 ( ext{T}) 掉了。
如果一个代码不行,就考虑换个种子吧。
srand(...);
为了获得更精确的解,也可以把 (d) 和 (T_0) 调的更精准一点
const double d = 0.996 -> 0.99996;
const double lim = 1e-10 -> 1e-15;
还有,随机乱搞一些 初温,终温,降温系数 也是可以的。
随机微调:
对于序列分组这类问题,每次可以随机两个位置交换计算新解的贡献。
但要注意如果没有接受这个状态时要把两个位置在交换回去。
打乱排序:
对于一些统计贡献与序列顺序无关的题可以考虑。
函数 random_shuffle() 可以在 (O(n)) 的时间内随机打乱一个序列
包含在 ctime 中,使用方法和 sort 类似。
可以用下面那道 P2503 来练练手。
Tips
模拟退火通常用来解决一些数据范围比较小,但对正解的计算不好算的问题。
通过随机一些状态来不断逼近正解。
其计算过程通常是 简单粗暴 的。
其正确性可能是 玄学 的。
这些例题中都有体现,注意体会。
例题
UVA10228 A Star not a Tree?
初始点的位置考虑选择所有点的平均值(人类本质?)
按照上面说的每次随机一个点即可。
如何计算一个点的贡献?(n) 的数据范围只有 (100),暴力计算即可。
看一下代码可能会更好理解。
/*
Work by: Suzt_ilymics
Problem: 不知名屑题
Knowledge: 垃圾算法
Time: O(能过)
CAQ yyds !!!!
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
#include<ctime>
#define LL long long
#define orz cout<<"lkp AK IOI!"<<endl
using namespace std;
const int MAXN = 1e5+5;
const int INF = 1e9+7;
const int mod = 1e9+7;
const double d = 0.996;
const double lim = 1e-10;
int n;
double ax[MAXN], ay[MAXN];
double limx, limy; // 上一次选择保留的位置
double ansx, ansy; // 存答案的位置;
double ans;
int read(){
int s = 0, f = 0;
char ch = getchar();
while(!isdigit(ch)) f |= (ch == '-'), ch = getchar();
while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
return f ? -s : s;
}
double dis(double sx, double sy, double ex, double ey) {
return sqrt((sx - ex) * (sx - ex) + (sy - ey) * (sy - ey));
}
double calc(double sx, double sy) {
double sum = 0.0;
for(int i = 1; i <= n; ++i) {
sum += dis(sx, sy, ax[i], ay[i]);
}
return sum;
}
void SA() {
double T = 2021; // 设置初始温度
while(T > lim) { // 当没降完温继续降温
double nowx = limx + ((rand() << 1) - RAND_MAX) * T; // 独特的随机一个点的公式
double nowy = limy + ((rand() << 1) - RAND_MAX) * T;
double now = calc(nowx, nowy);//计算贡献
double del = now - ans; // 计算 改变量
if(del < 0) {
ansx = nowx, ansy = nowy;
limx = nowx, limy = nowy;
ans = now;
} else if(exp(-del / T) > (double)rand() / RAND_MAX) { // 概率的选择接受这个解
limx = nowx, limy = nowy;
}
T *= d; // 降温
}
}
void work() {
limx /= (1.0 * n); // 取一个平均值
limy /= (1.0 * n);
ansx = limx, ansy = limy;
ans = calc(limx, limy);
for(int i = 1; i <= 10; ++i) SA(); // 多执行几遍 SA 函数
}
int main()
{
int t = read();
for(int i = 1; i < t; ++i) { // UVA 独特的数据测试方式
limx = limy = ansx = ansy = 0.0;
ans = 0;
n = read();
for(int j = 1; j <= n; ++j) {
scanf("%lf%lf", &ax[j], &ay[j]);
limx += ax[j], limy += ay[j];
}
work();
printf("%.0lf
", ans);
}
n = read();
for(int j = 1; j <= n; ++j) {
scanf("%lf%lf", &ax[j], &ay[j]);
limx += ax[j], limy += ay[j];
}
work();
printf("%.0lf
", ans);
return 0;
}
P5544 [JSOI2016]炸弹攻击1
肯定要先随机一个点,考虑如何确定 (R)。
随机吗?
注意随机一个量的时候只能有一个参照量,也就是说这里不能同时随机点的位置和爆炸半径。
因为我们无法简单的确定一个决策依据。
人类本质?
能炸多少炸多少啊!
所以暴力找到最大爆炸范围统计贡献就行啊。
/*
Work by: Suzt_ilymics
Problem: 不知名屑题
Knowledge: 垃圾算法
Time: O(能过)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
#include<cstdlib>
#include<ctime>
#define LL long long
#define orz cout<<"lkp AK IOI!"<<endl
using namespace std;
const int MAXN = 1e5+5;
const int INF = 1e9+7;
const int mod = 1e9+7;
const double d = 0.996;
const double lim = 1e-10;
struct node {
int x, y, r;
}a[MAXN];
struct node2 {
int x, y;
}b[MAXN];
int n, m, R;
double limx, limy, ansx, ansy;
int ans;
int read(){
int s = 0, f = 0;
char ch = getchar();
while(!isdigit(ch)) f |= (ch == '-'), ch = getchar();
while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
return f ? -s : s;
}
double GetR(double sx, double sy, int x) {
return sqrt((sx - a[x].x) * (sx - a[x].x) + (sy - a[x].y) * (sy - a[x].y)) - a[x].r;
}
double Dis(double sx, double sy, int x) {
return sqrt((sx - b[x].x) * (sx - b[x].x) + (sy - b[x].y) * (sy - b[x].y));
}
int calc(double sx, double sy) {
double maxR = 1.0 * R;
for(int i = 1; i <= n; ++i) {
maxR = min(maxR, GetR(sx, sy, i));
}
int cnt = 0;
for(int i = 1; i <= m; ++i) {
if(Dis(sx, sy, i) <= maxR) cnt++;
}
return cnt;
}
void SA() {
double T = 2021;
while(T > lim) {
double nowx = limx + ((rand() << 1) - RAND_MAX) * T;
double nowy = limy + ((rand() << 1) - RAND_MAX) * T;
int now = calc(nowx, nowy);
int del = now - ans;
if(del > 0) {
ansx = nowx, ansy = nowy;
limx = nowx, limy = nowy;
ans = now;
} else if(exp(-del/T) < (double) rand() / RAND_MAX) {
limx = nowx, limy = nowy;
}
T *= d;
}
}
void work() {
ansx = ansy = limx = limy = 0.0;
ans = calc(limx, limy);
while((double)clock() / CLOCKS_PER_SEC < 0.70) SA(); // CLOCKS_PER_SEC
}
int main()
{
n = read(), m = read(), R = read();
for(int i = 1; i <= n; ++i) a[i].x = read(), a[i].y = read(), a[i].r = read();
for(int i = 1; i <= m; ++i) b[i].x = read(), b[i].y = read();
work();
printf("%d", ans);
return 0;
}
P2503 [HAOI2006]均分数据
原题面中的式子可能有点错误,应该把 (m) 组当成 (m) 个元素来计算方差
介绍一个函数 random_shuffle(),可以在 (O(n)) 的时间内,将一段区间随机打乱。
考虑最简单的想法,
每次随机打乱,贪心的分组。
每次加进一个元素,将它放进当前 (m) 组中最小的那一组中。
然后计算贡献。
多随机几遍,总有一遍我们会碰到最优解的。
/*
Work by: Suzt_ilymics
Problem: 不知名屑题
Knowledge: 垃圾算法
Time: O(能过)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
#include<ctime>
#define LL long long
#define orz cout<<"lkp AK IOI!"<<endl
using namespace std;
const int MAXN = 1e5+5;
const int INF = 1e9+7;
const int mod = 1e9+7;
const double d = 0.996;
const double lim = 1e-10;
int n, m;
int a[22];
int b[7];
int sum;
double ave, ans = 10000000.0;
int read(){
int s = 0, f = 0;
char ch = getchar();
while(!isdigit(ch)) f |= (ch == '-'), ch = getchar();
while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
return f ? -s : s;
}
double calc() {
memset(b, false, sizeof b);
for(int i = 1; i <= n; ++i) {
int wz = 1;
for(int j = 1; j <= m; ++j) if(b[wz] > b[j]) wz = j;
b[wz] += a[i];
}
double Sum = 0;
for(int i = 1; i <= m; ++i) {
Sum += (ave - 1.0 * b[i]) * (ave - 1.0 * b[i]);
}
Sum /= (1.0 * m);
return sqrt(Sum);
}
void SA() {
double T = 2021;
while(T > lim) {
random_shuffle(a + 1, a + n + 1);
double now = calc();
ans = min(ans, now);
// double del = now - ans;
//// cout<<now<<endl;
// if(del < 0) {
// ans = now;
// }
T *= d;
}
}
void work() {
ave = 1.0 * sum / m;
for(int i = 1; i <= 20; ++i) SA();
}
int main()
{
n = read(), m = read();
for(int i = 1; i <= n; ++i) a[i] = read(), sum += a[i];
work();
printf("%.2lf", ans);
return 0;
}
P3878 [TJOI2010]分金币
前一半分一组,后一半分一组。
然后每次随机两个位置交换一下计算贡献。
nowx = rand() % n + 1; // 整数位置的随机直接 % n + 1 即可
这里与板子略有不同
如果更优就更新,
否则考虑概率接受,
否则你要把元素再换回去!
计算函数应该很好想,依旧是暴力,如果还不会就看代码吧。
/*
Work by: Suzt_ilymics
Problem: 不知名屑题
Knowledge: 垃圾算法
Time: O(能过)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
#include<ctime>
#define int long long
#define LL long long
#define orz cout<<"lkp AK IOI!"<<endl
using namespace std;
const int MAXN = 1e5+5;
const int INF = 1e12+7;
const int mod = 1e9+7;
const double d = 0.996;
const double lim = 1e-10;
int t, n, ans = INF;
int a[40];
int read(){
int s = 0, f = 0;
char ch = getchar();
while(!isdigit(ch)) f |= (ch == '-'), ch = getchar();
while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
return f ? -s : s;
}
int calc() {
int sum1 = 0, sum2 = 0;
for(int i = 1; i <= n / 2; ++i) sum1 += a[i];
for(int i = n / 2 + 1; i <= n; ++i) sum2 += a[i];
return abs(sum1 - sum2);
}
void SA() {
double T = 2021;
while(T > lim) {
int nowx = rand() % n + 1;
int nowy = rand() % n + 1;
swap(a[nowx], a[nowy]);
int now = calc();
int del = now - ans;
if(del < 0) {
ans = now;
} else if(exp(-del/T) > (double)rand() / RAND_MAX) {
} else swap(a[nowx], a[nowy]);
T *= d;
}
}
void work() {
for(int i = 1; i <= 100; ++i) SA();
}
signed main()
{
t = read();
while(t--) {
n = read();
ans = INF;
for(int i = 1; i <= n; ++i) a[i] = read();
random_shuffle(a + 1, a + n + 1);
work();
printf("%lld
", ans);
}
return 0;
}
P3936 Coloring
选择按顺序染色作为初始状态。
然后开始微调。
如何更快的计算贡献?
在原来的基础上减去两个位置原来位置的贡献,然后加上交换后的贡献。
推荐参数:
d = 0.9999,lim = 1e-15,T = 500,srand(20041011)
这样的话分数就可以在 (97pts) 以上了
有个疑问?
我计算 (del) 的时候是当前值与交换前的值作差,而不是和最优值作差。可前面几道题都是和最优值作差,可这道题这样做却死活过不去。有没有大佬可以解释一下啊,也可以到我这个帖子看一看。
/*
Work by: Suzt_ilymics
Problem: 不知名屑题
Knowledge: 垃圾算法
Time: O(能过)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
#include<ctime>
#define LL long long
#define orz cout<<"lkp AK IOI!"<<endl
using namespace std;
const int MAXN = 1e5+5;
const int INF = 1e9+7;
const int mod = 1e9+7;
const double d = 0.99998;
const double lim = 1e-15;
int dx[] = {1, -1, 0, 0};
int dy[] = {0, 0, 1, -1};
int n, m, c, ans, now_;
int p[55], cnt[55], top = 1;
int col[22][22], acol[22][22];
int read(){
int s = 0, f = 0;
char ch = getchar();
while(!isdigit(ch)) f |= (ch == '-'), ch = getchar();
while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
return f ? -s : s;
}
bool check(int x, int y) { return x < 1 || y < 1 || x > n || y > m; }
int Dev(int sx, int sy) {
int Cnt = 0;
for(int i = 0; i < 4; ++i) {
int x = sx + dx[i], y = sy + dy[i]; // 找相邻的四个格子计算贡献
if(check(x, y)) continue;
if(col[sx][sy] != col[x][y]) Cnt++;
}
return Cnt;
}
//int Dev(int x, int y) { return (col[x][y] != col[x-1][y] && x!=1) + (col[x][y] != col[x][y-1] && y!=1) + (col[x][y] != col[x+1][y] && x != n) + (col[x][y] != col[x][y+1] && y != m); }
int calc(int sx, int sy, int ex, int ey) {
int res = 0;
// orz;
res = res - Dev(sx, sy) - Dev(ex, ey); // 减去原来的贡献
swap(col[sx][sy], col[ex][ey]);
res = res + Dev(sx, sy) + Dev(ex, ey); // 加上现在的贡献
return res;
}
void SA() {
// orz;
// for(int i = 1; i <= n; ++i) for(int j = 1; j <= m; ++j) col[i][j] = acol[i][j];
// now_ = ans;
double T = 500;
while(T > lim) {
int nowsx = rand() % n + 1;
int nowsy = rand() % m + 1;
int nowex = rand() % n + 1;
int nowey = rand() % m + 1;
// int pre = Calc();
// swap(col[nowsx][nowsy], col[nowex][nowey]); // 先交换
// cout<<calc(nowsx, nowsy, nowex, nowey)<<"
";
int now = now_ + calc(nowsx, nowsy, nowex, nowey); // 再计算
// cout<<ans<<" "<<now_<<" "<<now<<"
";
int del = now - now_; // now_ 存的是当前 col 矩阵的答案
// int del = now - ans; // ans 存的是最优解
if(del < 0) { // 更新这个解
ans = now;
now_ = now;
for(int i = 1; i <= n; ++i) for(int j = 1; j <= m; ++j) acol[i][j] = col[i][j];
} else if(exp(-del/T) > (double) rand() / RAND_MAX) {
now_ = now; // 一定概率接受当前这个状态
} else {
swap(col[nowsx][nowsy], col[nowex][nowey]); // 交换回去
}
T *= d;
}
}
void work() {
// for(int i = 1; i <= n; ++i) {
// for(int j = 1; j <= m; ++j) {
// ans += Dev(i, j);
// }
// }
// ans /= 2;
for(int i = 2; i <= n; ++i)
for(int j = 1;j <= m; ++j)
if(col[i][j] != col[i - 1][j]) ans++;
for(int i = 1; i <= n; ++i)
for(int j = 2;j <= m; ++j)
if(col[i][j] != col[i][j - 1]) ans++;
now_ = ans;
// cout<<ans<<" "<<now_<<endl;
// cout<<ans<<endl;
// for(int i = 1; i <= 30; ++i) SA();
while((double)clock() / CLOCKS_PER_SEC < 3.90) SA();//, cout<<ans<<" "<<now_<<endl;
}
int main()
{
srand(20041011);
n = read(), m = read(), c = read();
for(int i = 1; i <= c; ++i) p[i] = read();
for(int i = 1; i <= n; ++i) {
for(int j = 1; j <= m; ++j) {
if(cnt[top] == p[top]) ++top;
acol[i][j] = col[i][j] = top;
++cnt[top];
}
}
work();
// printf("%d
", ans);
for(int i = 1; i <= n; ++i) {
for(int j = 1; j <= m; ++j) {
printf("%d ", acol[i][j]);
}puts("");
}
return 0;
}
/*
int dev(int sx, int sy, int ex, int ey) {
int cnt = 0;
for(int i = 0; i < 4; ++i) {
int x = sx + dx[i], y = sy + dy[i]; // 与起点相邻的点
if(check(x, y)) continue;
if(col[ex][ey] != col[x][y]) cnt++;
}
for(int i = 0; i < 4; ++i) {
int x = ex + dx[i], y = ey + dy[i]; // 与终点相邻的点
if(check(x, y)) continue;
if(col[sx][sy] != col[x][y]) cnt++;
}
// cout<<"cnt1 :"<< cnt<<" ";
return cnt;
}
int Calc() {
int cnt = 0;
for(int i = 2; i <= n; ++i)
for(int j = 1;j <= m; ++j)
if(col[i][j] != col[i - 1][j]) cnt++;
for(int i = 1; i <= n; ++i)
for(int j = 2;j <= m; ++j)
if(col[i][j] != col[i][j - 1]) cnt++;
return cnt;
}
*/