比赛时候切了A-E,fst了A
Standings第一页只有三个人挂了A题,而我就是其中之一,真™开心啊蛤蛤蛤
A. Fake NP
Tavak and Seyyed are good friends. Seyyed is very funny and he told Tavak to solve the following problem instead of longest-path.
You are given l and r. For all integers from l to r, inclusive, we wrote down all of their integer divisors except 1. Find the integer that we wrote down the maximum number of times.
Solve the problem to show that it's not a NP problem.
The first line contains two integers l and r (2 ≤ l ≤ r ≤ 109).
Print single integer, the integer that appears maximum number of times in the divisors.
If there are multiple answers, print any of them.
19 29
2
3 6
3
Definition of a divisor: https://www.mathsisfun.com/definitions/divisor-of-an-integer-.html
The first example: from 19 to 29 these numbers are divisible by 2: {20, 22, 24, 26, 28}.
The second example: from 3 to 6 these numbers are divisible by 3: {3, 6}.
脑洞题
求被[l,r]范围的数拥有的最多的因数。
如果l==r就输出l,如果l<r就输出2,正确性显然
只要5行就可以AC呢
1 #include<iostream> 2 #include<cstdio> 3 using namespace std; 4 int main(){ 5 int l,r; 6 scanf("%d%d",&l,&r); 7 if(l==r)printf("%d ",l); 8 else printf("2 "); 9 return 0; 10 }
看到题的时候蠢兮兮枚举sqrt范围内的数,算1~r的贡献减去1~l-1的贡献。
其实这样也可以龟速跑过的吧?但是减的时候减了1~l的贡献,PP以后还自信锁题试图hack别人,这就回天无力了。(PP都是骗人的)
In the beginning of the new year Keivan decided to reverse his name. He doesn't like palindromes, so he changed Naviek to Navick.
He is too selfish, so for a given n he wants to obtain a string of n characters, each of which is either 'a', 'b' or 'c', with no palindromes of length 3 appearing in the string as a substring. For example, the strings "abc" and "abca" suit him, while the string "aba" doesn't. He also want the number of letters 'c' in his string to be as little as possible.
The first line contains single integer n (1 ≤ n ≤ 2·105) — the length of the string.
Print the string that satisfies all the constraints.
If there are multiple answers, print any of them.
2
aa
3
bba
A palindrome is a sequence of characters which reads the same backward and forward.
看上去是个贪心递推?假的!
abbaabbaabba无限循环即可
或者"aabb"也可以

1 #include<iostream> 2 #include<algorithm> 3 #include<cstring> 4 #include<cstdio> 5 #include<cmath> 6 using namespace std; 7 const int mxn=200010; 8 int read(){ 9 int x=0,f=1;char ch=getchar(); 10 while(ch<'0' || ch>'9'){if(ch=='-')f=-1;ch=getchar();} 11 while(ch>='0' && ch<='9'){x=x*10+ch-'0';ch=getchar();} 12 return x*f; 13 } 14 char s[mxn]; 15 int n; 16 bool check(int i,char c){ 17 if(s[i-1]==c)return 0; 18 return 1; 19 } 20 int main(){ 21 int i,j; 22 n=read(); 23 for(i=1;i<=n;i++){ 24 if(i%4==1)printf("a"); 25 else if(i%4==2)printf("b"); 26 else if(i%4==3)printf("b"); 27 else if(i%4==0)printf("a"); 28 } 29 printf(" "); 30 return 0; 31 }
C. Find Amir
构造题真开心
代价是$ mod (n+1) $意义下计算的,脑洞一下可以发现1 to n , 2 to n-1 3 to n-2 这样的走法代价为0,而n to 2,n-1 to 3这样的转移代价是1
于是这样转转转就可以了,再考虑到总共有奇数个点的情况,答案为(n+1)/2-1

1 #include<iostream> 2 #include<algorithm> 3 #include<cstring> 4 #include<cstdio> 5 #include<cmath> 6 using namespace std; 7 int read(){ 8 int x=0,f=1;char ch=getchar(); 9 while(ch<'0' || ch>'9'){if(ch=='-')f=-1;ch=getchar();} 10 while(ch>='0' && ch<='9'){x=x*10+ch-'0';ch=getchar();} 11 return x*f; 12 } 13 int main(){ 14 int i,j; 15 int n=read(); 16 if(n==1)printf("0 "); 17 else{ 18 printf("%d ",(n+1)/2-1); 19 } 20 return 0; 21 }
D. Minimum number of steps
发现如果有连续的一串a后面一个b,它们对答案的贡献是$(2^cnt[a])-1$
cnt是要累积的,因为前面的ab换成bba以后,如果后面还有b,仍然对答案有贡献

1 #include<iostream> 2 #include<algorithm> 3 #include<cstring> 4 #include<cstdio> 5 #include<cmath> 6 #define LL long long 7 using namespace std; 8 const int mod=1e9+7; 9 const int mxn=1000010; 10 int read(){ 11 int x=0,f=1;char ch=getchar(); 12 while(ch<'0' || ch>'9'){if(ch=='-')f=-1;ch=getchar();} 13 while(ch>='0' && ch<='9'){x=x*10+ch-'0';ch=getchar();} 14 return x*f; 15 } 16 int ksm(int a,int k){ 17 int res=1; 18 while(k){ 19 if(k&1)res=(LL)res*a%mod; 20 a=(LL)a*a%mod; 21 k>>=1; 22 } 23 return res; 24 } 25 char s[mxn]; 26 int main(){ 27 int i,j; 28 scanf("%s",s+1); 29 int n=strlen(s+1); 30 int ans=0,cnt=0; 31 for(i=1;i<=n;i++){ 32 if(s[i]=='a'){ 33 cnt++; 34 } 35 else if(cnt){ 36 ans=((LL)ans+ksm(2,cnt)%mod-1)%mod; 37 // cnt--; 38 } 39 } 40 printf("%d ",ans); 41 return 0; 42 }
E. Ice cream coloring
Isart and Modsart were trying to solve an interesting problem when suddenly Kasra arrived. Breathless, he asked: "Can you solve a problem I'm stuck at all day?"
We have a tree T with n vertices and m types of ice cream numerated from 1 to m. Each vertex i has a set of si types of ice cream. Vertices which have the i-th (1 ≤ i ≤ m) type of ice cream form a connected subgraph. We build a new graph G with m vertices. We put an edge between the v-th and the u-th (1 ≤ u, v ≤ m, u ≠ v) vertices in G if and only if there exists a vertex in T that has both the v-th and the u-th types of ice cream in its set. The problem is to paint the vertices of G with minimum possible number of colors in a way that no adjacent vertices have the same color.
Please note that we consider that empty set of vertices form a connected subgraph in this problem.
As usual, Modsart don't like to abandon the previous problem, so Isart wants you to solve the new problem.
The first line contains two integer n and m (1 ≤ n, m ≤ 3·105) — the number of vertices in T and the number of ice cream types.
n lines follow, the i-th of these lines contain single integer si (0 ≤ si ≤ 3·105) and then si distinct integers, each between 1 and m — the types of ice cream in the i-th vertex. The sum of si doesn't exceed 5·105.
n - 1 lines follow. Each of these lines describes an edge of the tree with two integers u and v (1 ≤ u, v ≤ n) — the indexes of connected by this edge vertices.
Print single integer c in the first line — the minimum number of colors to paint the vertices in graph G.
In the second line print m integers, the i-th of which should be the color of the i-th vertex. The colors should be between 1 and c. If there are some answers, print any of them.
3 3
1 1
2 2 3
1 2
1 2
2 3
2
1 1 2
4 5
0
1 1
1 3
3 2 4 5
2 1
3 2
4 3
3
1 1 1 2 3
In the first example the first type of ice cream is present in the first vertex only, so we can color it in any color. The second and the third ice cream are both presented in the second vertex, so we should paint them in different colors.
In the second example the colors of the second, the fourth and the fifth ice cream should obviously be distinct.
贪心 构造 读题
开这题的时候还有1h10min,看了几遍题面没看懂,觉得接下来一个小时都要砸这题上了。
转去看F,觉得如果做不出E那肯定也做不出F。
这时候我注意到我的A题有BUG,但是我已经把它锁了。
实时rank900+,如果不再肝一道题出来就是大幅掉分预定
单纵就是干!斩杀靠砸桶!(大雾)
懵逼了半小时,然后敲了个乱搞代码居然真的乱搞出来了,蛤蛤蛤
这题卡读题啊……看那个我标成红色的句子,大致意思就是说,同种标号的冰淇淋挤在树的连通块上,它是解题的关键。
注意到每个树结点内包含的冰淇淋构成一个完全图,它们的颜色必定不一样。
脑洞一下可以得出最少需要的颜色数是max{一个结点包含的冰淇淋数}
由于上面那个性质,暴力DFS贪心染色不会有问题

1 #include<iostream> 2 #include<algorithm> 3 #include<cstring> 4 #include<cstdio> 5 #include<cmath> 6 #include<vector> 7 using namespace std; 8 const int mxn=300005; 9 int read(){ 10 int x=0,f=1;char ch=getchar(); 11 while(ch<'0' || ch>'9'){if(ch=='-')f=-1;ch=getchar();} 12 while(ch>='0' && ch<='9'){x=x*10+ch-'0';ch=getchar();} 13 return x*f; 14 } 15 struct edge{ 16 int v,nxt; 17 }e[mxn<<1]; 18 int hd[mxn],mct=0; 19 void add_edge(int u,int v){ 20 e[++mct].v=v;e[mct].nxt=hd[u];hd[u]=mct;return; 21 } 22 int n,m,ans; 23 int col[mxn]; 24 vector<int>ve[mxn]; 25 bool vis[mxn]; 26 int st[mxn],top=0; 27 void DFS(int u,int fa){ 28 int cnt=1,t;top=1; 29 for(int i=0;i<ve[u].size();i++){ 30 t=ve[u][i]; 31 if(col[t])st[++top]=t,vis[col[t]]=1; 32 } 33 for(int i=0;i<ve[u].size();i++){ 34 t=ve[u][i]; 35 if(!col[t]){ 36 while(vis[cnt])cnt++; 37 col[t]=cnt; 38 cnt++; 39 } 40 } 41 while(top)vis[col[st[top--]]]=0; 42 for(int i=hd[u];i;i=e[i].nxt){ 43 int v=e[i].v; 44 if(v==fa)continue; 45 DFS(v,u); 46 } 47 return; 48 } 49 int main(){ 50 int i,j,s,u,v; 51 n=read();m=read(); 52 ans=1; 53 for(i=1;i<=n;i++){ 54 s=read(); 55 ans=max(ans,s); 56 for(j=1;j<=s;j++) 57 ve[i].push_back(read()); 58 } 59 for(i=1;i<n;i++){ 60 u=read();v=read(); 61 add_edge(u,v);add_edge(v,u); 62 } 63 DFS(1,0); 64 printf("%d ",ans); 65 for(i=1;i<=m;i++)if(!col[i])col[i]=1; 66 for(i=1;i<=m;i++){ 67 printf("%d ",col[i]); 68 } 69 return 0; 70 }
F. Expected diameter of a tree
Pasha is a good student and one of MoJaK's best friends. He always have a problem to think about. Today they had a talk about the following problem.
We have a forest (acyclic undirected graph) with n vertices and m edges. There are q queries we should answer. In each query two vertices v and u are given. Let V be the set of vertices in the connected component of the graph that contains v, and U be the set of vertices in the connected component of the graph that contains u. Let's add an edge between some vertex  and some vertex in
and some vertex in  and compute the value d of the resulting component. If the resulting component is a tree, the value d is the diameter of the component, and it is equal to -1 otherwise. What is the expected value of d, if we choose vertices a and b from the sets uniformly at random?
and compute the value d of the resulting component. If the resulting component is a tree, the value d is the diameter of the component, and it is equal to -1 otherwise. What is the expected value of d, if we choose vertices a and b from the sets uniformly at random?
Can you help Pasha to solve this problem?
The diameter of the component is the maximum distance among some pair of vertices in the component. The distance between two vertices is the minimum number of edges on some path between the two vertices.
Note that queries don't add edges to the initial forest.
The first line contains three integers n, m and q(1 ≤ n, m, q ≤ 105) — the number of vertices, the number of edges in the graph and the number of queries.
Each of the next m lines contains two integers ui and vi (1 ≤ ui, vi ≤ n), that means there is an edge between vertices ui and vi.
It is guaranteed that the given graph is a forest.
Each of the next q lines contains two integers ui and vi (1 ≤ ui, vi ≤ n) — the vertices given in the i-th query.
For each query print the expected value of d as described in the problem statement.
Your answer will be considered correct if its absolute or relative error does not exceed 10 - 6. Let's assume that your answer is a, and the jury's answer is b. The checker program will consider your answer correct, if  .
.
3 1 2
1 3
3 1
2 3
-1
2.0000000000
5 2 3
2 4
4 3
4 2
4 1
2 5
-1
2.6666666667
2.6666666667
In the first example the vertices 1 and 3 are in the same component, so the answer for the first query is -1. For the second query there are two options to add the edge: one option is to add the edge 1 - 2, the other one is 2 - 3. In both ways the resulting diameter is 2, so the answer is 2.
In the second example the answer for the first query is obviously -1. The answer for the second query is the average of three cases: for added edges 1 - 2 or 1 - 3 the diameter is 3, and for added edge 1 - 4 the diameter is 2. Thus, the answer is  .
.
这题太菜啦!我只用了整整一上午时间就写出来啦!
数学问题 数学期望 树形DP 并查集
用并查集可以判连通块,并且搞出连通块的size
树形DP可以处理出每个点出发能走的最远距离g[](用于计算直径)
询问两个点的时候,如果在同一个连通块里输出-1 (废话)
否则找到这两个点对应的树。假设在两棵树上分别选一点得到u,v,如果g[u]+g[v]+1大于原树直径,那么贡献就是g[u]+g[v]+1,否则贡献是原树直径。
计算每种方案的贡献res, $ans=res/(size[find(u)]*size[find(v)])$
将同一棵树的g[]从小到大排序以后用two pointers扫描可以优化上述过程,做到$ O(n) $计算,或者排序后二分$O(nlogn)$
再加个记忆化就能过了

1 #include<iostream> 2 #include<algorithm> 3 #include<cstring> 4 #include<cstdio> 5 #include<cmath> 6 #include<map> 7 #include<vector> 8 using namespace std; 9 const double eps=1e-7; 10 const int mxn=100010; 11 int read(){ 12 int x=0,f=1;char ch=getchar(); 13 while(ch<'0' || ch>'9'){if(ch=='-')f=-1;ch=getchar();} 14 while(ch>='0' && ch<='9'){x=x*10+ch-'0';ch=getchar();} 15 return x*f; 16 } 17 struct edge{ 18 int v,nxt; 19 }e[mxn<<1]; 20 int hd[mxn],mct=0; 21 void add_edge(int u,int v){ 22 e[++mct].v=v;e[mct].nxt=hd[u];hd[u]=mct;return; 23 } 24 int fa[mxn],sz[mxn]; 25 int vis[mxn]; 26 int find(int x){ 27 return fa[x]==x?x:fa[x]=find(fa[x]); 28 } 29 // 30 vector<int> D[mxn],smm[mxn]; 31 int dis[mxn],g[mxn]; 32 #define amax(a,b) ((a)>(b))?(a):(b) 33 void DFS(int u,int ff){ 34 for(int i=hd[u],v;i;i=e[i].nxt){ 35 v=e[i].v; if(v==ff)continue; 36 DFS(v,u); 37 dis[u]=amax(dis[u],dis[v]+1); 38 } 39 return; 40 } 41 inline void update(int *a,int x){ 42 for(int i=0;i<2;i++) 43 if(x>a[i])swap(a[i],x); 44 return; 45 } 46 void DFS2(int u,int ff,int up,vector<int> &now){ 47 int ano[2];//通往u的其他子树的最长/次长链 48 ano[0]=ano[1]=-1000; 49 vis[u]=1; 50 g[u]=amax(dis[u],up);//从u出发能走的最远距离 51 now.push_back(g[u]); 52 // 53 for(int i=hd[u];i;i=e[i].nxt){ 54 int v=e[i].v;if(v==ff)continue; 55 update(ano,dis[v]); 56 } 57 for(int i=hd[u],v;i;i=e[i].nxt){ 58 v=e[i].v;if(v==ff)continue; 59 int tmp=(ano[0]==dis[v])?ano[1]:ano[0]; 60 DFS2(v,u,amax(tmp+2,up+1),now); 61 } 62 return; 63 } 64 65 #undef amax 66 int n,m,Q; 67 map<pair<int,int>,double>mp; 68 void calc(int u,int v){ 69 if(mp.count(make_pair(u,v))){ 70 printf("%.10f ",mp[make_pair(u,v)]); 71 return; 72 } 73 if(sz[u]<sz[v])swap(u,v); 74 int L=max(D[u].back(),D[v].back()); 75 double res=0.0; 76 int K=D[u].size(); 77 for(int i=0;i<D[v].size();i++){ 78 int x=upper_bound(D[u].begin(),D[u].end(),L-D[v][i]-1)-D[u].begin(); 79 res+=1.0*x*L+(smm[u][K]-smm[u][x])+1.0*(K-x)*(D[v][i]+1); 80 } 81 res/=D[u].size();res/=D[v].size(); 82 if(u>v)swap(u,v); 83 mp[make_pair(u,v)]=res; 84 printf("%.10f ",res); 85 return; 86 } 87 int main(){ 88 int i,j,u,v; 89 n=read();m=read();Q=read(); 90 for(i=1;i<=n;i++)fa[i]=i,sz[i]=1; 91 for(i=1;i<=m;i++){ 92 u=read();v=read(); 93 add_edge(u,v);add_edge(v,u); 94 u=find(u);v=find(v); 95 if(u==v)continue; 96 fa[v]=u; 97 sz[u]+=sz[v]; 98 } 99 for(i=1;i<=n;i++) 100 if(find(i)==i)DFS(i,0); 101 for(i=1;i<=n;i++){ 102 if(!vis[i]){ 103 int x=find(i); 104 DFS2(x,0,0,D[x]); 105 sort(D[x].begin(),D[x].end()); 106 int ed=D[x].size(); 107 smm[x].resize(ed+1); 108 for(j=1;j<=ed;j++) 109 smm[x][j]=smm[x][j-1]+D[x][j-1]; 110 } 111 } 112 while(Q--){ 113 u=read();v=read(); 114 u=find(u);v=find(v); 115 if(u==v){ 116 printf("-1 "); 117 continue; 118 } 119 if(u>v)swap(u,v); 120 calc(u,v); 121 } 122 return 0; 123 }

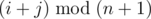 and can be used multiple times. Help Sajjad to find the minimum cost he needs to pay for tickets to visit all schools. He can start and finish in any school.
and can be used multiple times. Help Sajjad to find the minimum cost he needs to pay for tickets to visit all schools. He can start and finish in any school.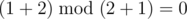 .
.