Submit: 1653 Solved: 835
Description
有一张N×m的数表，其第i行第j列（1 < =i < =礼，1 < =j < =m）的数值为
能同时整除i和j的所有自然数之和。给定a，计算数表中不大于a的数之和。
Input
输入包含多组数据。
输入的第一行一个整数Q表示测试点内的数据组数，接下来Q行，每行三个整数n，m，a(|a| < =10^9)描述一组数据。
Output
对每组数据，输出一行一个整数，表示答案模2^31的值。
Sample Input
2
4 4 3
10 10 5
4 4 3
10 10 5
Sample Output
20
148
148
HINT
1 < =N．m < =10^5 ， 1 < =Q < =2×10^4
Source
数学 容斥 莫比乌斯反演
【能同时整除i和j的所有自然数之和】也就是gcd(i,j)的所有因数的和。
设x的所有因数的和为F,则F(x)=$ sum_{d|x}^{x}d $
迁移这里的思想 http://www.cnblogs.com/SilverNebula/p/6582843.html 可以求出一定范围内有多少数对的gcd等于特定值
不看那个链接也没关系，我打算再写一遍
设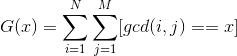
，即N,M范围内gcd(i,j)==x的数对的数量
——————太长不看的一部分推导——————
(暂时懒得写)
————————————
则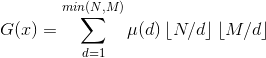 
←此处N和M均为原N、M除以x（懒得重作图了）
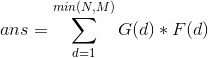
一番变形得
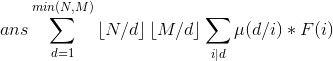
后面那个sigma里的东西可以预处理出来。
如何解决题目中a的限制呢？
将询问离线，按a从小到大排序，回答每个询问时，把值小于a的F(x)都添加进来，其他的F(x)置为0。这一操作可以用树状数组维护
跑了1w+ms，之后看popoQQQ dalao的题解说这个模数可以直接自然溢出……于是删掉了所有longlong和取模，可以跑3700+ms
1 /*by SilverN*/ 2 #include<algorithm> 3 #include<iostream> 4 #include<cstring> 5 #include<cstdio> 6 #include<cmath> 7 #include<vector> 8 #define LL long long 9 using namespace std; 10 const int mxn=100005; 11 int read(){ 12 int x=0,f=1;char ch=getchar(); 13 while(ch<'0' || ch>'9'){if(ch=='-')f=-1;ch=getchar();} 14 while(ch>='0' && ch<='9'){x=x*10+ch-'0';ch=getchar();} 15 return x*f; 16 } 17 struct F{ 18 int pos; 19 int v; 20 bool operator < (F b)const{ 21 return v<b.v; 22 } 23 }f[mxn]; 24 int pri[mxn],mu[mxn],cnt=0; 25 bool vis[mxn]; 26 void init(){ 27 mu[1]=1; 28 for(int i=2;i<mxn;i++){ 29 if(!vis[i]){ 30 pri[++cnt]=i; 31 mu[i]=-1; 32 } 33 for(int j=1;j<=cnt && (LL)pri[j]*i<mxn;j++){ 34 vis[pri[j]*i]=1; 35 if(i%pri[j]==0){mu[pri[j]*i]=0;break;} 36 mu[pri[j]*i]=-mu[i]; 37 } 38 } 39 for(int i=1;i<mxn;i++){//计算因数和 40 f[i].pos=i; 41 for(int j=i;j<mxn;j+=i) 42 f[j].v+=i; 43 } 44 sort(f+1,f+mxn); 45 return; 46 } 47 // 48 int t[mxn]; 49 int ed; 50 void add(int x,int v){ 51 while(x<=ed){t[x]+=v;x+=x&-x;} 52 return; 53 } 54 int ask(int x){ 55 int res=0; 56 while(x){res=res+t[x];x-=x&-x;} 57 return res&0x7fffffff; 58 } 59 struct que{ 60 int n,m,a; 61 int id; 62 }q[mxn]; 63 inline int cmp(const que x,const que y){return x.a<y.a;} 64 int n; 65 int ans[mxn]; 66 int calc(int a,int b){ 67 int res=0;int pos; 68 if(a>b)swap(a,b); 69 for(int i=1;i<=a;i=pos+1){ 70 int x=a/i,y=b/i; 71 pos=min(a/x,b/y); 72 res+=x*y*(ask(pos)-ask(i-1)); 73 } 74 return res&0x7fffffff; 75 } 76 void solve(int x){ 77 ans[q[x].id]=calc(q[x].m,q[x].n); 78 return; 79 } 80 int main(){ 81 int i,j; 82 init();ed=mxn; 83 n=read(); 84 for(i=1;i<=n;i++){ 85 q[i].n=read();q[i].m=read();q[i].a=read(); 86 q[i].id=i; 87 } 88 sort(q+1,q+n+1,cmp); 89 int hd=1; 90 for(i=1;i<=n;i++){ 91 while(hd<mxn && f[hd].v<=q[i].a){ 92 for(j=f[hd].pos;j<mxn;j+=f[hd].pos){ 93 add(j,f[hd].v*mu[j/f[hd].pos]); 94 } 95 hd++; 96 } 97 solve(i); 98 } 99 for(i=1;i<=n;i++) 100 printf("%d ",ans[i]&0x7fffffff); 101 return 0; 102 } 103 //&2147483647 104 /* 105 3 106 500 800 239 107 2798 2389 9023 108 1200 100000 20000 109 */