题目描述
又到暑假了,住在城市A的Car想和朋友一起去城市B旅游。她知道每个城市都有四个飞机场,分别位于一个 矩形的四个顶点上,同一个城市中两个机场之间有一条笔直的高速铁路,第I个城市中高速铁路了的单位里程价格为Ti,任意两个不同城市的机场之间均有航线, 所有航线单位里程的价格均为t。
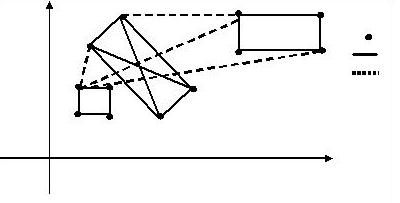
图例(从上而下)
机场 高速铁路
飞机航线
注意:图中并没有
标出所有的铁路与航线。
那么Car应如何安排到城市B的路线才能尽可能的节省花费呢?她发现这并不是一个简单的问题,于是她来向你请教。
找出一条从城市A到B的旅游路线,出发和到达城市中的机场可以任意选取,要求总的花费最少。
输入输出格式
输入格式:第一行为一个正整数n(0<=n<=10),表示有n组测试数据。
每组的第一行有四个正整数s,t,A,B。
S(0<S<=100)表示城市的个数,t表示飞机单位里程的价格,A,B分别为城市A,B的序号,(1<=A,B<=S)。
接下来有S行,其中第I行均有7个正整数xi1,yi1,xi2,yi2,xi3,yi3,Ti,这当中的(xi1,yi1),(xi2,yi2),(xi3,yi3)分别是第I个城市中任意三个机场的坐标,T I为第I个城市高速铁路单位里程的价格。
输出格式:共有n行,每行一个数据对应测试数据。 保留一位小数
输入输出样例
输入样例#1:
1
3 10 1 3
1 1 1 3 3 1 30
2 5 7 4 5 2 1
8 6 8 8 11 6 3
输出样例#1:
47.5
最短路。
对于每个城市,根据已知的三个点坐标算出第四个点坐标,然后在同一城市的点之间两两连边(高铁),在不同城市的点之间两两连边(飞机),跑最短路即可。如何算第四个点的坐标?
首先由于四个点构成矩形,已知的三个点必构成直角三角形。通过比较三条边的长度可以找到直角顶点。具体看代码。
1 /*by SilverN*/ 2 #include<algorithm> 3 #include<iostream> 4 #include<cstring> 5 #include<cstdio> 6 #include<cmath> 7 #include<queue> 8 using namespace std; 9 const int mxn=24000; 10 int read(){ 11 int x=0,f=1;char ch=getchar(); 12 while(ch<'0' || ch>'9'){if(ch=='-')f=-1;ch=getchar();} 13 while(ch>='0' && ch<='9'){x=x*10+ch-'0';ch=getchar();} 14 return x*f; 15 } 16 double dist(int x1,int y1,int x2,int y2){ 17 return sqrt( (double)(x1-x2)*(x1-x2)+(double)(y1-y2)*(y1-y2) ); 18 } 19 struct node{//点集 20 int x,y; 21 }a[mxn],p[5]; 22 int ncnt=0; 23 int pdd(){//找直角边顶点 24 double d12=dist(p[1].x,p[1].y,p[2].x,p[2].y); 25 double d23=dist(p[3].x,p[3].y,p[2].x,p[2].y); 26 double d13=dist(p[1].x,p[1].y,p[3].x,p[3].y); 27 if(d12>d23 && d12>d13)return 3; 28 if(d23>d12 && d23>d13)return 1; 29 if(d13>d23 && d13>d12)return 2; 30 } 31 void pos4(int tp){//算第四个点坐标 32 switch(tp){//根据直角顶点讨论。其实如果先把直角顶点swap到p[1]位置,代码可以更精简 33 case 1:{ 34 p[4].x=p[2].x+p[3].x-p[1].x; 35 p[4].y=p[2].y+p[3].y-p[1].y; 36 break; 37 } 38 case 2:{ 39 p[4].x=p[3].x+p[1].x-p[2].x; 40 p[4].y=p[3].y+p[1].y-p[2].y; 41 break; 42 } 43 case 3:{ 44 p[4].x=p[2].x+p[1].x-p[3].x; 45 p[4].y=p[2].y+p[1].y-p[3].y; 46 break; 47 } 48 } 49 return; 50 } 51 struct edge{ 52 int v,nxt; 53 double dis; 54 }e[mxn]; 55 int hd[mxn],mct=0; 56 void add_edge(int u,int v,double dis){ 57 e[++mct].v=v;e[mct].dis=dis;e[mct].nxt=hd[u];hd[u]=mct; 58 return; 59 } 60 61 int N; 62 int n,w,A,B; 63 64 queue<int>q; 65 double dis[mxn]; 66 bool inq[mxn]; 67 void SPFA(int s){//最短路 68 for(int i=1;i<=ncnt;i++)dis[i]=10000009; 69 dis[s]=0;inq[s]=1; 70 q.push(s); 71 int i,j; 72 while(!q.empty()){ 73 int u=q.front();q.pop();inq[u]=0; 74 for(i=hd[u];i;i=e[i].nxt){ 75 int v=e[i].v; 76 if(dis[v]>dis[u]+e[i].dis){ 77 dis[v]=dis[u]+e[i].dis; 78 if(!inq[v]){ 79 inq[v]=1; 80 q.push(v); 81 } 82 } 83 } 84 } 85 return; 86 } 87 int main(){ 88 int i,j; 89 N=read(); 90 while(N--){ 91 memset(a,0,sizeof a); 92 memset(e,0,sizeof e); 93 memset(hd,0,sizeof hd); 94 mct=ncnt=0; 95 // 96 n=read(); 97 w=read();A=read();B=read(); 98 int X1,X2,X3,Y1,Y2,Y3,tt; 99 for(i=1;i<=n;++i){ 100 p[1].x=read();p[1].y=read(); 101 p[2].x=read();p[2].y=read(); 102 p[3].x=read();p[3].y=read(); 103 tt=read(); 104 pos4(pdd()); 105 for(j=1;j<=4;j++) 106 for(int k=1;k<=4;k++){ 107 if(k!=j)add_edge(ncnt+j,ncnt+k,dist(p[j].x,p[j].y,p[k].x,p[k].y)*tt); 108 } 109 for(j=1;j<=4;j++){ 110 for(int k=1;k<=ncnt;k++){ 111 double dd=dist(p[j].x,p[j].y,a[k].x,a[k].y)*w; 112 add_edge(ncnt+j,k,dd); 113 add_edge(k,ncnt+j,dd); 114 } 115 } 116 for(j=1;j<=4;j++){a[++ncnt]=p[j];} 117 } 118 double ans=100000009; 119 int st=(A-1)*4; 120 for(i=1;i<=4;i++){ 121 SPFA(st+i); 122 int ed=(B-1)*4; 123 for(j=1;j<=4;j++){ 124 // printf("%d to %d dis:%.1f ",st+i,ed+j,dis[ed+j]); 125 ans=min(ans,dis[ed+j]); 126 } 127 } 128 printf("%.1f ",ans); 129 } 130 return 0; 131 }