POJ1330 Nearest Common Ancestors

 

Nearest Common Ancestors

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 24587		Accepted: 12779

Description

A rooted tree is a well-known data structure in computer science and engineering. An example is shown below: 

 
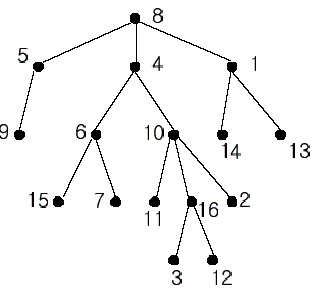
In the figure, each node is labeled with an integer from {1, 2,...,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is. 

For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y. 

Write a program that finds the nearest common ancestor of two distinct nodes in a tree. 

Input

The input consists of T test cases. The number of test cases (T) is given in the first line of the input file. Each test case starts with a line containing an integer N , the number of nodes in a tree, 2<=N<=10,000. The nodes are labeled with integers 1, 2,..., N. Each of the next N -1 lines contains a pair of integers that represent an edge --the first integer is the parent node of the second integer. Note that a tree with N nodes has exactly N - 1 edges. The last line of each test case contains two distinct integers whose nearest common ancestor is to be computed.

Output

Print exactly one line for each test case. The line should contain the integer that is the nearest common ancestor.

Sample Input

2
16
1 14
8 5
10 16
5 9
4 6
8 4
4 10
1 13
6 15
10 11
6 7
10 2
16 3
8 1
16 12
16 7
5
2 3
3 4
3 1
1 5
3 5

Sample Output

4
3

Source

Taejon 2002

LCA（最近公共祖先）

先找到树根，之后倍增处理出每个点的祖先结点，然后同时上溯即可。

//lca 
#include<algorithm>
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<vector>
using namespace std;
const int mxn=10010;
int n;
vector<int> e[mxn];
int fa[mxn][18];
int dep[mxn];
int in[mxn];
void add_edge(int u,int v){
    e[u].push_back(v);
    in[v]++;
}
void dfs(int u){//求点深度，倍增算祖先结点fa 
    for(int i=0;i<e[u].size();i++){
        int v=e[u][i];
        fa[v][0]=u;
        dep[v]=dep[u]+1;
        for(int j=1;(1<<j)<=dep[v];j++){
            fa[v][j]=fa[fa[v][j-1]][j-1];
        }
        dfs(v);
    }
    return;
}
int lca(int a,int b){
    if(dep[a]<dep[b])swap(a,b);//（处理深度更大的那个） 
    for(int i=16;i!=-1;i--)//从高位开始试。（其实从低开始也一样？） 
        if(dep[a]>=dep[b]+(1<<i))a=fa[a][i];//此步结束后，a和b查找到的深度相同 
    if(a==b)return a;
    for(int i=16;i!=-1;i--)//共同上溯 
        if(fa[a][i]!=fa[b][i])a=fa[a][i],b=fa[b][i];
    return fa[a][0];
}
int main(){
    int T;
    scanf("%d",&T);
    int i,j;
    while(T--){
        memset(dep,0,sizeof(dep));
        memset(fa,0,sizeof(fa));
        memset(in,0,sizeof(in));
        scanf("%d",&n);
        for(i=1;i<=n;i++) e[i].clear();
        int u,v;
        for(i=1;i<n;i++){
            scanf("%d%d",&u,&v);
            add_edge(u,v);
        }
        int root=0;
        for(i=1;i<=n;i++)if(in[i]==0){root=i;break;}//入度为0的那个点是根 
        dep[root]=1;
        fa[root][0]=-1;
        dfs(root);
        int a,b;
        scanf("%d%d",&a,&b);
        printf("%d
",lca(a,b));
    }
    return 0;
}