最大独立集专题
本文着重介绍一些特别的图的有关最大独立集的问题。
part1.树上最大独立集
例题:没有上司的舞会
题目描述
某大学有N个职员,编号为1~N。他们之间有从属关系,也就是说他们的关系就像一棵以校长为根的树,父结点就是子结点的直接上司。现在有个周年庆宴会,宴会每邀请来一个职员都会增加一定的快乐指数Ri,但是呢,如果某个职员的上司来参加舞会了,那么这个职员就无论如何也不肯来参加舞会了。所以,请你编程计算,邀请哪些职员可以使快乐指数最大,求最大的快乐指数。
输入格式
第一行一个整数N。(1<=N<=6000)
接下来N行,第i+1行表示i号职员的快乐指数Ri。(-128<=Ri<=127)
接下来N-1行,每行输入一对整数L,K。表示K是L的直接上司。
最后一行输入0 0
输出格式
输出最大的快乐指数。
输入输出样例
输入 #1
7
1
1
1
1
1
1
1
1 3
2 3
6 4
7 4
4 5
3 5
0 0
输出 #1
5
方法:树形dp
这就是典型的树上带权最大独立集。(这水题居然有这么高大尚的名字)
直接树形dp即可。
(dp[x][0/1])表示选/不选第x个点的最大快乐度。
代码:
#include<bits/stdc++.h>
using namespace std;
int dp[10010][2],n,A[10010];
vector<int> G[10010];
void DFS(int x,int fa){
dp[x][1]=A[x];
for(int i=0;i<G[x].size();i++){
int t=G[x][i];
if(t==fa)continue;
DFS(t,x);
dp[x][0]+=max(dp[t][0],dp[t][1]);
dp[x][1]+=dp[t][0];
}
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%d",&A[i]);
for(int i=1;i<=n-1;i++){
int x,y;
scanf("%d %d",&x,&y);
G[x].push_back(y);
G[y].push_back(x);
}
DFS(1,0);
cout<<max(dp[1][0],dp[1][1]);
return 0;
}
part2.基环树最大独立集
基环树,也是环套树,简单地讲就是树上在加一条边。它形如一个环,环上每个点都有一棵子树的形式。因此,对基环树的处理大部分就是对树处理和对环处理。显然,难度在于后者。
例题1:天黑请闭眼
题目描述
最近天黑请闭眼在 C国十分流行!游戏里有两个身份,一个是杀手,另一个是平民。杀手知道哪些人是杀手,而平民对此一无所知。
现在为了知道谁是杀手,参与游戏的每个人都指证了一个人为杀手,可以确定的是,**杀手一定会指证平民**,而平民指证的人有可能是杀手,也有可能是平民。给出每位玩家指证的人,请找出游戏中最多可能的杀手个数。
输入
第一行包括一个整数N,表示玩家个数.玩家分别被编号为1~N.
接下来N行,每行一个整数,其中第K行的数表示编号为K的玩家所指证为杀手的玩家编号。
输出
输出仅一行,表示最多可能的杀手个数。
样例输入
7
3
3
4
5
6
4
4
3
2
3
1
3
2
1
1
样例输出
4
1
2
方法1:树形dp
显然,你会发现,题目中的边是可以无向的。因为x和其指向的人如果其中一人是狼,那么另一人必定不是狼。
于是,这就可以转化成基环树最大不带权独立集。
根据引用的内容,我们可以把基环树分成树和一条返祖边。
因此,我们抛开这条返祖边不看,剩下的就变成了一棵树。那么我们直接在树上dp即可。
而对于这条返祖边,其无非就是多了个限制,即与其相连的两个端点不能同时为狼。
于是,我们考虑,枚举一个端点是否为狼,然后dp两次即可。
注意:由于此题可能会形成基环树森林,所以对于每个基环树要分别dp,然后把答案累加。
代码:
#include<bits/stdc++.h>
#define MAXN 100010
using namespace std;
int n,nex[MAXN],pre[MAXN],tot,head[MAXN],deep[MAXN],ans,dp[MAXN][2],dp2[MAXN][2];
bool vis[MAXN],vis2[MAXN];
struct node {
int ed,last;
} G[MAXN*4];
void Add(int st,int ed) {
tot++;
G[tot]=node {ed,head[st]};
head[st]=tot;
}
int st,ed;
void DFS(int x,int fa) {//找环
deep[x]=deep[fa]+1;
for(int i=head[x]; i; i=G[i].last) {
int t=G[i].ed;
if(t==fa)continue;
if(deep[t]) {
if(deep[t]<deep[x])st=t,ed=x;
continue;
}
DFS(t,x);
}
}
void solve1(int x,int fa){//dp1:其中一个端点一定为狼
dp[x][1]=1;
vis[x]=true;
for(int i=head[x];i;i=G[i].last){
int t=G[i].ed;
if(t==fa)continue;
if(deep[t]!=deep[x]+1)continue;
if(vis[t])continue;
solve1(t,x);
dp[x][0]+=max(dp[t][0],dp[t][1]);
dp[x][1]+=dp[t][0];
}
if(nex[x]==x)dp[x][1]=-1e9-7;
if(x==ed)dp[x][1]=-1e9-7;
}
void solve2(int x,int fa){//dp2:其中一个端点一定不为狼
dp2[x][1]=1;
vis2[x]=true;
for(int i=head[x];i;i=G[i].last){
int t=G[i].ed;
if(t==fa)continue;
if(deep[t]!=deep[x]+1)continue;
if(vis2[t])continue;
solve2(t,x);
dp2[x][0]+=max(dp2[t][0],dp2[t][1]);
dp2[x][1]+=dp2[t][0];
}
if(nex[x]==x)dp2[x][1]=-1e9-7;
if(x==ed)dp2[x][0]=-1e9-7;
if(x==st)dp2[x][1]=-1e9-7;
}
int main() {
scanf("%d",&n);
for(int i=1; i<=n; i++)scanf("%d",&nex[i]),Add(nex[i],i),Add(i,nex[i]);
for(int i=1;i<=n;i++){
if(!deep[i]){
int tmp=0;
DFS(i,0);
solve1(i,0);
solve2(i,0);
tmp=max(tmp,dp[i][0]);
tmp=max(tmp,dp[i][1]);
tmp=max(tmp,dp2[i][0]);
tmp=max(tmp,dp2[i][1]);
ans+=tmp;
}
}
cout<<ans;
return 0;
}
方法2:贪心
如果我们把边当成有向的,那么会出现什么情况呢?
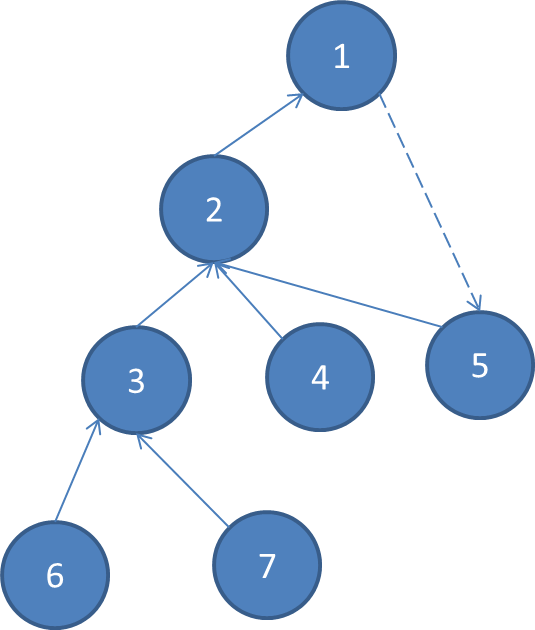
你会发现:
1.任意一个节点,其出度仅为1,但入度大于等于1。
2.任意一条边所连的两个端点,必定有一个点为狼。(如果两个点都不为狼,那么显然可以让一个点成为狼)
结合这两个性质,那么对于一条边x和其指向的y,如果x可以成为狼,那让x变成狼一定是更优的。(因为可能会有好多个点同时指向y,如果y成为狼,那么那些点显然都不能成为狼了,而让x成为狼,仅仅是y不能成为狼)
于是我们就先对这张图进行一波拓扑排序,对于一个点,若其未被标记,那么就选择他,并且把它指向的点标记(初始所有点都是未被标记)
而由于这是一棵基环树,所以剩下的必定是一个环,而对于环的话,我们可以把其划分成好多个未被标记的区间,然后每个区间可以成为狼的数量就是区间内点的数量/2.
注意:
1.对于一个区间,若其是遇到了被标记的点而停止更新的,那么要把点的数量+1,举个栗子:
一个环:1->2->3->4->1,如果4被标记了,那么我们统计区间内点的数量的答案为3,算出来3/2=1,但实际上这是可以选1和3的,所以要把数量+1。
2.首尾区间要合并统计,举个栗子:
依然是一个环1->2->3->4->1,如果3被标记了,那么第一次统计答案为2,加1为3,狼的数量为3/2=1;第二次统计答案为1,这时不能+1了,狼的数量为1/2=0,总计为1,但实际上是可以选2和4的,所以我们要把首尾合并在一起,即把第一次和第二次统计的答案加起来,算出来为(3+1)/2=2
虽然细节多了点,但是代码长度和时间还是很优秀滴。
代码:
#include<bits/stdc++.h>
#define MAXN 500010
using namespace std;
int n,nex[MAXN],deg[MAXN],ans,len1,len2;
bool can[MAXN],flag;
queue<int> Q;
int main() {
memset(can,true,sizeof(can));
scanf("%d",&n);
for(int i=1; i<=n; i++)scanf("%d",&nex[i]),deg[nex[i]]++;
for(int i=1; i<=n; i++)if(!deg[i])Q.push(i);
while(!Q.empty()){
int now=Q.front();
Q.pop();
ans+=can[now];
deg[nex[now]]--;
if(can[now])can[nex[now]]=false;
if(!deg[nex[now]])Q.push(nex[now]);
}
for(int i=1,x; i<=n; i++) {
flag=true,len1=len2=0;
if(deg[i]) {
x=i;
do{
deg[x]=0;
if(flag)len1++;
else len2++;
if(!can[x])ans+=len2/2,len2=0,flag=false;
x=nex[x];
}while(x!=i);
ans+=(len1+len2)/2;
}
}
cout<<ans;
return 0;
}
写法对比:
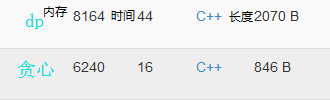
反思:没有上司的舞会也可以贪心吗?
显然,很麻烦的。之所以可以贪心,是因为这是不带权的最大独立集,而对于带权的话,选它的所有儿子不一定是最优的。
所以遇到这类最大独立集题目的话,我认为写dp比较保险,毕竟贪心用处不广并且细节多,不写对拍的话基本上很难调出来。
例题2:【HDU】P4830 Party
Problem Description
B公司共有N个员工,但是并不是所有人都能和睦相处。在每一个人的心中都有一个潜在的对手,任何人都不能接受和他的对手同时参加B公司的聚餐。然而这种关系并不一定是对称的,也就是说,A把B视作自己的对手,而B所想的对手并不一定是A。
现在,B公司准备举办一次盛大的聚会,公司希望员工通过这次聚会获得尽可能多的快乐值。第i个员工的快乐值是一个大于0不大于100的整数,如果他参加聚餐,他就会获得的快乐值,如果他的对手参加聚餐,他的快乐值就为0。
但老板在安排聚餐时不知道如何解决这个问题,因此,他找到你帮忙计算这次聚会最多可以带来多少快乐值。
Input
输入数据的第一行是一个整数T,表示有T组测试数据。
每组数据的第一行包括一个整数N,表示共有N个员工。(约有500组数据N不大于500,约有10组数据N不大于100000)
第二行是N个用空格隔开的整数,第i个整数表示第i个员工的对手的编号。数据保证 xi ∈ [1,N], 且 xi <> i .
第三行也包含N个用空格隔开的整数,表示第i个员工能够获得的快乐值ai。
Output
对于第k组数据,第一行输出Case #k:,第二行输出仅包含一个数,表示这次聚会最多可以带来多少快乐值。
Sample Input
1
8
2 7 1 8 4 2 3 5
50 30 40 40 50 10 70 60
Sample Output
Case #1:
190
Hint
在样例中,应选择1、6、7、8号员工。
方法:树形dp
这仅仅就多了个权值而已,把不带权的稍微改一下就好了。
代码:
#include<bits/stdc++.h>
#define MAXN 100010
using namespace std;
int n,nex[MAXN],pre[MAXN],tot,head[MAXN],deep[MAXN],ans,dp[MAXN][2],dp2[MAXN][2],A[MAXN],T,cas;
bool vis[MAXN],vis2[MAXN];
struct node {
int ed,last;
} G[MAXN*4];
void Add(int st,int ed) {
tot++;
G[tot]=node {ed,head[st]};
head[st]=tot;
}
int st,ed;
void DFS(int x,int fa) {
deep[x]=deep[fa]+1;
for(int i=head[x]; i; i=G[i].last) {
int t=G[i].ed;
if(t==fa)continue;
if(deep[t]) {
if(deep[t]<deep[x])st=t,ed=x;
continue;
}
DFS(t,x);
}
}
void solve1(int x,int fa) {
dp[x][1]=A[x];
vis[x]=true;
for(int i=head[x]; i; i=G[i].last) {
int t=G[i].ed;
if(t==fa)continue;
if(deep[t]!=deep[x]+1)continue;
if(vis[t])continue;
solve1(t,x);
dp[x][0]+=max(dp[t][0],dp[t][1]);
dp[x][1]+=dp[t][0];
}
if(nex[x]==x)dp[x][1]=-1e9-7;
if(x==ed)dp[x][1]=-1e9-7;
}
void solve2(int x,int fa) {
dp2[x][1]=A[x];
vis2[x]=true;
for(int i=head[x]; i; i=G[i].last) {
int t=G[i].ed;
if(t==fa)continue;
if(deep[t]!=deep[x]+1)continue;
if(vis2[t])continue;
solve2(t,x);
dp2[x][0]+=max(dp2[t][0],dp2[t][1]);
dp2[x][1]+=dp2[t][0];
}
if(nex[x]==x)dp2[x][1]=-1e9-7;
if(x==ed)dp2[x][0]=-1e9-7;
if(x==st)dp2[x][1]=-1e9-7;
}
void init(){
st=ed=tot=ans=0;
memset(G,0,sizeof(G));
memset(dp,0,sizeof(dp));
memset(dp2,0,sizeof(dp2));
memset(deep,0,sizeof(deep));
memset(head,0,sizeof(head));
memset(vis,false,sizeof(vis));
memset(vis2,false,sizeof(vis2));
memset(pre,0,sizeof(pre));
}
int main() {
scanf("%d",&T);
while(T--) {
init();
scanf("%d",&n);
for(int i=1; i<=n; i++)scanf("%d",&nex[i]),Add(nex[i],i),Add(i,nex[i]);
for(int i=1; i<=n; i++)scanf("%d",&A[i]);
for(int i=1; i<=n; i++) {
if(!deep[i]) {
int tmp=0;
DFS(i,0);
solve1(i,0);
solve2(i,0);
tmp=max(tmp,dp[i][0]);
tmp=max(tmp,dp[i][1]);
tmp=max(tmp,dp2[i][0]);
tmp=max(tmp,dp2[i][1]);
ans+=tmp;
}
}
printf("Case #%d:
%d
",++cas,ans);
}
return 0;
}
part3.仙人掌最大独立集
如果某个无向连通图的任意一条边至多只出现在一条简单回路(simple cycle)里,我们就称这张图为仙人图(cactus)。所谓简单回路就是指在图上不重复经过任何一个顶点的回路。
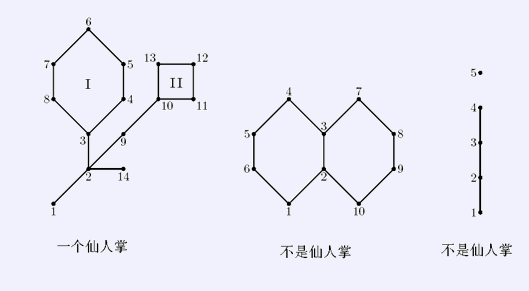
例题:【BZOJ】P4316 小C的独立集
Description
图论小王子小C经常虐菜,特别是在图论方面,经常把小D虐得很惨很惨。
这不,小C让小D去求一个无向图的最大独立集,通俗地讲就是:在无向图中选出若干个点,这些点互相没有边连接,并使取出的点尽量多。
小D虽然图论很弱,但是也知道无向图最大独立集是npc,但是小C很仁慈的给了一个很有特点的图: 图中任何一条边属于且仅属于一个简单环,图中没有重边和自环。小C说这样就会比较水了。
小D觉得这个题目很有趣,就交给你了,相信你一定可以解出来的。
Input
第一行,两个数n, m,表示图的点数和边数。
第二~m+1行,每行两个数x,y,表示x与y之间有一条无向边。
Output
输出这个图的最大独立集。
Sample Input
5 6
1 2
2 3
3 1
3 4
4 5
3 5
Sample Output
2
HINT
100% n <=50000, m<=60000
方法:dp
一道仙人掌不带权最大独立集。
由于仙人掌没有一条边是在两个环上,于是我们依然可以把其转化成树和若干条返祖边。
由于这里的返祖边有很多条,显然枚举端点状态时间是吃不消的。
由于一条返祖边会形成一个环,于是我们可以把dp过程分成树dp和环dp两部分。
如下图:
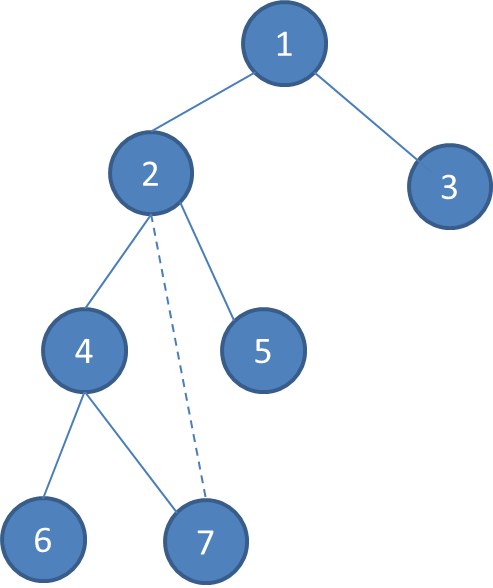
我们首先进行树dp,由于2,4,7构成了一个环那么我们再树dp过程中转移时不考虑这3个点,即4从不含7的所有儿子中转移过来,2从不含4的所有儿子中转移过来。
树dp部分代码:
void DFS(int x,int fa){
dp[x][1]=1;
dfsn[x]=low[x]=++mark;//我这里采用类似Tarjan缩点的方法去判断
pre[x]=fa;
deep[x]=deep[fa]+1;
for(int i=head[x];i;i=G[i].last){
int t=G[i].ed;
if(t==fa)continue;
if(deep[t]&&deep[t]!=deep[x]+1){
low[x]=min(low[x],dfsn[t]);
continue;
}
DFS(t,x);
low[x]=min(low[x],low[t]);
if(low[t]>dfsn[x]){
dp[x][0]+=max(dp[t][0],dp[t][1]);
dp[x][1]+=dp[t][0];
}
}
for(int i=head[x];i;i=G[i].last){//进行环dp必须保证该点是环的一端点
int t=G[i].ed;
if(t==fa)continue;
if(deep[t]==deep[x]+1)continue;
if(low[t]!=dfsn[x])continue;
DP2(x,t);//环dp
}
}
对于环dp的话,我们破环为链,再拿图来说,我们变成2->4->7这条链。
类似基环树的写法,我们枚举一端点(7)是否被选,然后进行两次链上dp。
而对于链dp的话,我们已经算出了一个点不包括这条链上的点的dp值,那么就变成了这个问题:
一个序列,选了当前数就不能选下一个数,每个数选和不选都分别有一个价值,求这个价值的最大值
那么,设(dp2[i][0/1])表示第i个数选/不选,前i个数的最大价值
转移方程:
其中(tmp[i])表示序列中第i个数对应的点的编号。
整体代码:
#include<bits/stdc++.h>
#define MAXN 100010
using namespace std;
int n,m,tot,head[MAXN],pre[MAXN],deep[MAXN],dp[MAXN][2],mark,dfsn[MAXN],low[MAXN],tmp[MAXN],dp2[MAXN][2],ans;
struct node{
int ed,last;
}G[MAXN<<1];
void Add(int st,int ed){
tot++;
G[tot]=node{ed,head[st]};
head[st]=tot;
}
void DP2(int st,int ed){
tmp[0]=0;
while(ed!=st)tmp[++tmp[0]]=ed,ed=pre[ed];
tmp[++tmp[0]]=st;
dp2[0][0]=dp2[0][1]=0;
for(int i=1;i<=tmp[0];i++){
dp2[i][0]=max(dp2[i-1][0],dp2[i-1][1])+dp[tmp[i]][0];
dp2[i][1]=dp2[i-1][0]+dp[tmp[i]][1];
}
dp[st][0]=dp2[tmp[0]][0];
dp2[0][0]=-1e9+7,dp2[0][1]=0;
for(int i=1;i<=tmp[0];i++){
dp2[i][0]=max(dp2[i-1][0],dp2[i-1][1])+dp[tmp[i]][0];
dp2[i][1]=dp2[i-1][0]+dp[tmp[i]][1];
}
dp[st][1]=dp2[tmp[0]][1];
}
void DFS(int x,int fa){
dp[x][1]=1;
dfsn[x]=low[x]=++mark;
pre[x]=fa;
deep[x]=deep[fa]+1;
for(int i=head[x];i;i=G[i].last){
int t=G[i].ed;
if(t==fa)continue;
if(deep[t]&&deep[t]!=deep[x]+1){
low[x]=min(low[x],dfsn[t]);
continue;
}
DFS(t,x);
low[x]=min(low[x],low[t]);
if(low[t]>dfsn[x]){
dp[x][0]+=max(dp[t][0],dp[t][1]);
dp[x][1]+=dp[t][0];
}
}
for(int i=head[x];i;i=G[i].last){
int t=G[i].ed;
if(t==fa)continue;
if(deep[t]==deep[x]+1)continue;
if(low[t]!=dfsn[x])continue;
DP2(x,t);
}
}
int main(){
scanf("%d %d",&n,&m);
for(int x,y,i=1;i<=m;i++){
scanf("%d %d",&x,&y);
Add(x,y);
Add(y,x);
}
for(int i=1;i<=n;i++){
if(!dfsn[i]){
DFS(i,0);
ans+=max(dp[i][0],dp[i][1]);
}
}
cout<<ans;
return 0;
}
变态题:【SDOI】2010 城市规划
题目描述
小猪iPig来到了一个叫做pigsty的城市里,pigsty是一座专门为小猪所准备的城市,城市里面一共有n个小区给小猪们居住,并且存在许多条无向边连接着许多小区。因为这里是一个和谐的城市,所以小猪iPig准备在这个城市里面度过他的余生。
若干年之后小猪iPig当上了规划局长,这件事令他非常开心。不过与此同时pigsty城市里面出现了许多反和谐主义者,他们已经厌烦了这样和谐的生活,在城市里到处闹事。小猪iPig为了更好地控制局面,他把城市改造成了另外一个样子:iPig把道路全部摧毁之后重新修建了m条无向边,并且保证每一个小区最多存在于一个由无向边组成的环中。
iPig以为这样做就让那些反和谐主义者不敢继续猖狂下去了,谁知到在新的城市道路修建好以后反和谐主义者宣言要对城市的小区进行一次洗脑!
这下可麻烦了,iPig赶紧收集了许多的情报。iPig给每个小区标记了一个和谐值HX_i,用它来表示第i个小区的和谐程度。
通过地下消息iPig又得知那些反和谐主义者进攻时有个规律:他们会选择若干个小区下手,这些小区都派一只猪过去,把这些小区的和谐值归零。在这个过程中,每个选择的小区所直接连接着的几个小区都派了一只猪去看守——以防被警猪给干扰。这个计划看似完美但是还是存在一个漏洞:因为人员之间都是在网络上认识的,互相没有见过面,为了防止不必要的麻烦(认错猪之类),每个小区最多只会有一头猪存在。
iPig突然感到了莫大的压力,他想知道在最坏情况下会丢失多少和谐值。但是不懂计算机的他不知道应该怎样计算。你能帮帮他吗?
输入格式
输入第一行有两个整数n和m,表示pigsty城市里面有n个小区,在iPig修整城市后有m条无向边连接着n个小区。
接下来一行有n个正整数,第i个正整数HX_i表示第i个小区的和谐值为HX_i。
接下来m行,每行两个正整数a和b(1<=a,b<=n),表示存在一条连接着小区a和小区 b的无向边。
输出格式
输出只有一行一个整数,表示最坏情况下损失的和谐值为多少。
输入输出样例
输入 #1
9 9
2 2 3 4 1 2 3 10 11
1 2
2 3
1 3
3 5
5 4
5 6
4 7
6 7
8 9
输出 #1
17
说明/提示
【样例解释】
反和谐主义者选择的小区分别是小区3(看守的小区是小区1、小区2和小区5)、小区7(看守的小区是小区4和小区6)和小区9(看守的小区是小区8),这样会损失的总和谐值为3+3+11=17。
或者选择的小区分别是小区1(看守的小区是小区2和小区3)、小区4(看守的小区是小区5和小区7)和小区9(看守的小区是小区8),这样会损失的总和谐值为2+4+11=17。
如果同时选择小区3、小区4和小区9,虽然损失的总和谐值为18,但是小区3和小区4都要派猪来看守小区5,这不符合条件,故此方案不可行。
【数据约定】
对于20%的数据,保证每个点不存在于任何一个环中;
对于另外30%的数据,保证图中只存在一个环;
对于100%的数据,有N<=1000000,M<=2000000,所有的权值不超过1000。
方法:还是dp
说白了,这道题就是这样:
仙人掌,带权,求一个权值最大的点的集合,使得任意两点之间的距离大于等于3
第一部分:树dp
我们设(dp[x][0/1/2])表示节点x自己选/有儿子选/自己和所有儿子都不选的最大权值。
树dp转移,((x)表示一个节点,(t)表示其儿子)。
其中(dp[x][0])的初值为x的权值
解释:
x自己选:那么只能从t自己和它所有儿子都不选的状态转移过来。
x有儿子选了:显然,x是不能有两个以上的儿子同时选的,所以我们就判断是保留当前x节点选的儿子还是t,取个max就好了。
x自己和儿子都不选:那么就从t中有儿子选了或者t中自己和儿子都不选中去一个最大值转移过来。
树dp代码:
void DFS(int x,int fa) {
dp[x][0]=A[x];
dfsn[x]=low[x]=++mark;
pre[x]=fa;
deep[x]=deep[fa]+1;
for(register int i=head[x]; i; i=G[i].last) {
int t=G[i].ed;
if(t==fa)continue;
if(deep[t]&&deep[t]!=deep[x]+1) {
low[x]=min(low[x],dfsn[t]);
continue;
}
DFS(t,x);
low[x]=min(low[x],low[t]);
can[x]=true;
if(low[t]>dfsn[x]) {
dp[x][0]+=dp[t][2];
dp[x][1]=max(dp[x][1]+dp[t][1],dp[x][2]+dp[t][0]);
dp[x][2]+=max(dp[t][1],dp[t][2]);
}
}
for(register int i=head[x]; i; i=G[i].last) {
int t=G[i].ed;
if(t==fa)continue;
if(deep[t]==deep[x]+1)continue;
if(low[t]!=dfsn[x])continue;
DP2(x,t);
}
}
第二部分:环dp
额,这部分的话细节就有点小多了。
老规矩,先上张图:
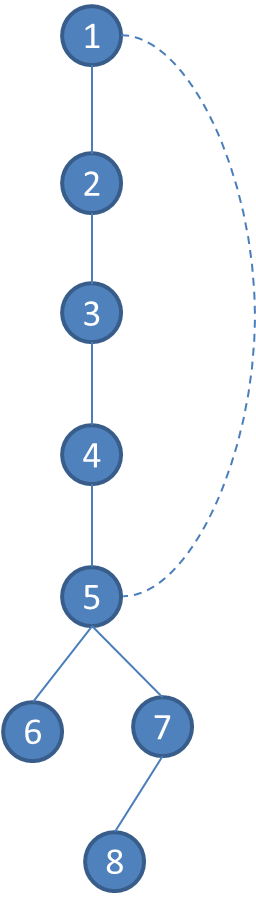
我们要分成以下几种情况讨论:
注:(len)表示这条链的长度
1.一端点(编号为5)自己选。
由于5选了,那么1的状态肯定就是有一个儿子选了,于是只能拿(dp2[len][2])来更新(dp[1][1])
2.一端点(编号为5)有一个儿子选了。
此时,5的儿子到1的距离为2。
同样的,我们拿(dp2[len][1])来更新(dp[1][1]),(dp2[len][2])来更新(dp[1][2])
3.一端点(编号为5)自己和儿子都不选。
此时,5的子树中到1的距离至少为3。
那我们就直接拿(dp2[len][0/1/2])来更新(dp[1][0/1/2])。
但是,这是错误的!!!
一组hack数据:
5 5
4 4 9 7 7
1 2
2 3
1 4
3 5
5 4out : 9
仔细想一想,你会发现,
在这种情况下,如果4被选了,那么4到1的距离就是2(通过返祖边)。
但实际上,在链上4到1的距离为3。
也就是说,这样处理,4和1会同时被选!
那好办,我们再枚举4是否被选。
综上,一共有这4种情况:
1.一端点自己选。
2.一端点有儿子选。
3.一端点自己和儿子都不选,但链上倒数第二个点自己选了。
4.一端点自己和儿子都不选,且链上倒数第二个点自己未选。
环dp部分代码:
void DP2(int st,int ed) {
int x=ed,ans0=0,ans1=0,ans2=0;
tmp[0]=0;
while(x!=st)tmp[++tmp[0]]=x,x=pre[x];
tmp[++tmp[0]]=st;
for(register int type=1; type<=4; ++type) {
dp2[1][0]=dp2[1][1]=dp2[1][2]=-2e18;
if(type==1)dp2[1][0]=dp[tmp[1]][0];
if(type==2)dp2[1][1]=dp[tmp[1]][1];
if(type==3||type==4)dp2[1][2]=dp[tmp[1]][2];
for(register int i=2; i<=tmp[0]; ++i) {
if(i==2&&type==3) {
dp2[2][1]=dp2[2][2]=-2e18;
dp2[2][0]=dp2[1][2]+max(A[tmp[2]],dp[tmp[2]][0]);
continue;
}
if(i==2&&type==4) {
dp2[2][0]=-2e18;
dp2[2][1]=dp2[1][0]+dp[tmp[2]][1];
dp2[2][2]=max(dp2[1][1],dp2[1][2])+dp[tmp[2]][2];
continue;
}
dp2[i][0]=dp2[i-1][2]+max(A[tmp[i]],dp[tmp[i]][0]);
dp2[i][1]=max(dp2[i-1][0]+dp[tmp[i]][2],dp2[i-1][1]+dp[tmp[i]][1]);
dp2[i][2]=max(dp2[i-1][1],dp2[i-1][2])+dp[tmp[i]][2];
}
if(type==1)ans1=max(ans1,dp2[tmp[0]][2]);
if(type==2)ans1=max(ans1,dp2[tmp[0]][1]),ans2=max(ans2,dp2[tmp[0]][2]);
if(type==3)ans1=max(ans1,dp2[tmp[0]][1]),ans2=max(ans2,dp2[tmp[0]][2]);
if(type==4)ans0=max(ans0,dp2[tmp[0]][0]),ans1=max(ans1,dp2[tmp[0]][1]),ans2=max(ans2,dp2[tmp[0]][2]);
}
dp[st][0]=ans0,dp[st][1]=ans1,dp[st][2]=ans2;
}
整体代码:
#include<bits/stdc++.h>
#define int long long
#define MAXN 1000010
using namespace std;
int n,m,tot,head[MAXN],pre[MAXN],deep[MAXN],dp[MAXN][3],mark,dfsn[MAXN],low[MAXN],tmp[MAXN],dp2[MAXN][3],ans,A[MAXN];
bool can[MAXN];
struct node {
int ed,last;
} G[MAXN<<1];
void Add(int st,int ed) {
tot++;
G[tot]=node {ed,head[st]};
head[st]=tot;
}
void DP2(int st,int ed) {
int x=ed,ans0=0,ans1=0,ans2=0;
tmp[0]=0;
while(x!=st)tmp[++tmp[0]]=x,x=pre[x];
tmp[++tmp[0]]=st;
for(register int type=1; type<=4; ++type) {
dp2[1][0]=dp2[1][1]=dp2[1][2]=-2e18;
if(type==1)dp2[1][0]=dp[tmp[1]][0];
if(type==2)dp2[1][1]=dp[tmp[1]][1];
if(type==3||type==4)dp2[1][2]=dp[tmp[1]][2];
for(register int i=2; i<=tmp[0]; ++i) {
if(i==2&&type==3) {
dp2[2][1]=dp2[2][2]=-2e18;
dp2[2][0]=dp2[1][2]+max(A[tmp[2]],dp[tmp[2]][0]);
continue;
}
if(i==2&&type==4) {
dp2[2][0]=-2e18;
dp2[2][1]=dp2[1][0]+dp[tmp[2]][1];
dp2[2][2]=max(dp2[1][1],dp2[1][2])+dp[tmp[2]][2];
continue;
}
dp2[i][0]=dp2[i-1][2]+max(A[tmp[i]],dp[tmp[i]][0]);
dp2[i][1]=max(dp2[i-1][0]+dp[tmp[i]][2],dp2[i-1][1]+dp[tmp[i]][1]);
dp2[i][2]=max(dp2[i-1][1],dp2[i-1][2])+dp[tmp[i]][2];
}
if(type==1)ans1=max(ans1,dp2[tmp[0]][2]);
if(type==2)ans1=max(ans1,dp2[tmp[0]][1]),ans2=max(ans2,dp2[tmp[0]][2]);
if(type==3)ans1=max(ans1,dp2[tmp[0]][1]),ans2=max(ans2,dp2[tmp[0]][2]);
if(type==4)ans0=max(ans0,dp2[tmp[0]][0]),ans1=max(ans1,dp2[tmp[0]][1]),ans2=max(ans2,dp2[tmp[0]][2]);
}
dp[st][0]=ans0,dp[st][1]=ans1,dp[st][2]=ans2;
}
void DFS(int x,int fa) {
dp[x][0]=A[x];
dfsn[x]=low[x]=++mark;
pre[x]=fa;
deep[x]=deep[fa]+1;
for(register int i=head[x]; i; i=G[i].last) {
int t=G[i].ed;
if(t==fa)continue;
if(deep[t]&&deep[t]!=deep[x]+1) {
low[x]=min(low[x],dfsn[t]);
continue;
}
DFS(t,x);
low[x]=min(low[x],low[t]);
can[x]=true;
if(low[t]>dfsn[x]) {
dp[x][0]+=dp[t][2];
dp[x][1]=max(dp[x][1]+dp[t][1],dp[x][2]+dp[t][0]);
dp[x][2]+=max(dp[t][1],dp[t][2]);
}
}
for(register int i=head[x]; i; i=G[i].last) {
int t=G[i].ed;
if(t==fa)continue;
if(deep[t]==deep[x]+1)continue;
if(low[t]!=dfsn[x])continue;
DP2(x,t);
}
}
signed main() {
scanf("%lld %lld",&n,&m);
for(register int i=1; i<=n; ++i)scanf("%lld",&A[i]);
for(register int x,y,i=1; i<=m; ++i) {
scanf("%lld %lld",&x,&y);
Add(x,y);
Add(y,x);
}
for(register int i=1; i<=n; ++i) {
if(!dfsn[i]) {
DFS(i,0);
ans+=max(max(dp[i][2],dp[i][0]),dp[i][1]);
}
}
cout<<ans;
return 0;
}