状压dp+容斥
由于n各集合有(2^n)个交集,因此我们可以把整个矩形划分成许多含有若干矩阵交集的子矩阵。
就像第一个样例就可以这样划分。
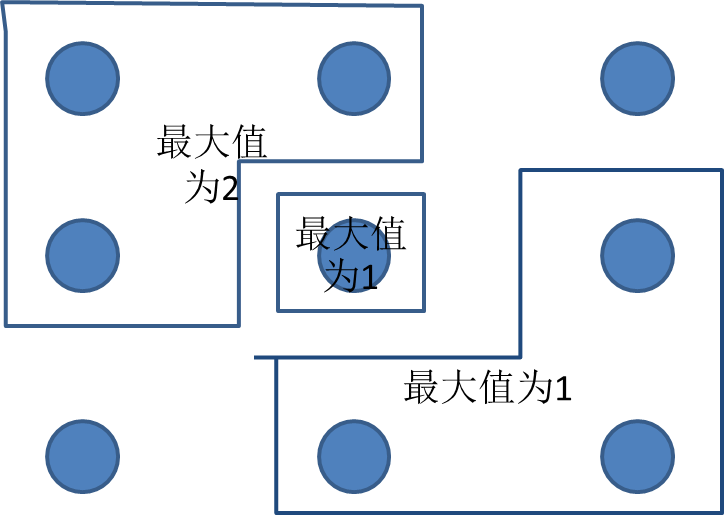
这样的话,我们就不用讨论许多矩阵相交的情况,问题就会简化很多。
设(mx[i])表示第i个子矩阵内的最大值, (S[i]) 表示第i个子矩阵内含有的元素数量
然后,我们考虑状压dp。对于一个子矩阵,我们有如下决策:
1.子矩阵内的最大值小于$mx[i] $,此时方案数为 ((mx[i]-1)^{S[i]}) 。
由于子矩阵是许多小矩阵的交集,只要一个小矩阵最大值达到了 (mx[i]),那么当前子矩阵实际最大值也为 (mx[i]),也是合法的。
2.子矩阵内的最大值为(mx[i]) ,此时方案数为 (mx[i]^{S[i]}-(mx[i]-1)^{S[i]}) 。由于子矩阵是许多小矩阵的交集,因此当前取到最大值可能会影响到一些其它小矩阵。
那么,(dp[i][j]) 表示前i个子矩阵,取得最大值的小矩阵状态为j的方案数
状态转移:
[dp[i][j]=dp[i][j]+dp[i-1][j] cdot (mx[i]-1)^{S[i]}
]
[dp[i][j|can[i]]=dp[i][j|can[i]]+dp[i-1][j]cdot mx[i]^{S[i]}-(mx[i]-1)^{S[i]}
]
其中(can[i])表示第i个子矩阵最大值取到 (mx[i]) 会使得哪些小矩阵达到最大值
而对于划分成许多子矩阵我们可以用容斥预处理一波。
注意:所有小矩阵的并集可能不为整个矩阵,也就是说,这种情况下,有若干个点是可以随便取的(就像样例1),我们最后还要乘以(m^{cnt})((cnt)表示可以随便取的点数量)
代码:
#include<bits/stdc++.h>
#define int long long
using namespace std;
int T,h,w,m,n,dp[(1<<10)+5][(1<<10)+5],MM[(1<<10)+5],cas,sum=0;
const int MOD=1e9+7;
struct Set{
int x1,y1,x2,y2,mx,SS;
int S(){
return max(x2-x1+1,0LL)*max(y2-y1+1,0LL);
}
}A[10010],B[10010];
Set operator + (Set X,Set Y){
Set Ans;
Ans.mx=min(X.mx,Y.mx);
Ans.x1=max(X.x1,Y.x1);
Ans.y1=max(X.y1,Y.y1);
Ans.x2=min(X.x2,Y.x2);
Ans.y2=min(X.y2,Y.y2);
return Ans;
}
int Quick_Pow(int a,int p){
int res=1;
while(p){
if(p&1)res=res*a%MOD;
a=a*a%MOD;
p>>=1;
}
return res;
}
signed main(){
scanf("%lld",&T);
while(T--){
memset(dp,0,sizeof(dp));
memset(A,0,sizeof(A));
memset(B,0,sizeof(B));
memset(MM,0,sizeof(MM));
scanf("%lld %lld %lld %lld",&h,&w,&m,&n);
A[0]=Set{1,1,h,w,2e9+7,0};
for(int i=1;i<=n;i++){
scanf("%lld %lld %lld %lld %lld",&B[(1<<(i-1))].x1,&B[(1<<(i-1))].y1,&B[(1<<(i-1))].x2,&B[(1<<(i-1))].y2,&B[(1<<(i-1))].mx);
}
for(int i=1;i<(1<<n);i++)A[i]=A[i-(i&-i)]+B[i&-i];
for(int i=(1<<n)-1;i>=0;i--){
A[i].SS=A[i].S();
for(int j=i+1;j<(1<<n);j++){
if((j|i)==j)A[i].SS-=A[j].SS;
}
for(int j=1;j<=n;j++){
if((1<<(j-1))&i){
if(A[i].mx==A[(1<<(j-1))].mx){
MM[i]|=(1<<(j-1));
}
}
}
}
dp[0][0]=1;
for(int i=1;i<(1<<n);i++){
for(int j=0;j<(1<<n);j++){
dp[i][j]+=dp[i-1][j]*Quick_Pow(A[i].mx-1,A[i].SS)%MOD,dp[i][j]%=MOD;
dp[i][j|MM[i]]+=dp[i-1][j]*(Quick_Pow(A[i].mx,A[i].SS)-Quick_Pow(A[i].mx-1,A[i].SS)+MOD)%MOD,dp[i][j|MM[i]]%=MOD;
}
}
sum=h*w;
for(int i=1;i<(1<<n);i++)sum-=A[i].SS;
printf("Case #%lld: %lld
",++cas,dp[(1<<n)-1][(1<<n)-1]*Quick_Pow(m,sum)%MOD);
}
return 0;
}