【BZOJ】P2144 跳跳棋

LCA+二分

看了题面，再看标签：二分也就算了，但。。。LCA？？
没错，就是LCA！
来慢慢分析一波。。。。。

由于一次只允许跳过1颗棋子并且两个棋子不能同时在一个点，我们以(1,2,3)为例((x,y,z)表示3个棋子分别在x,y和z位置)模拟一下.

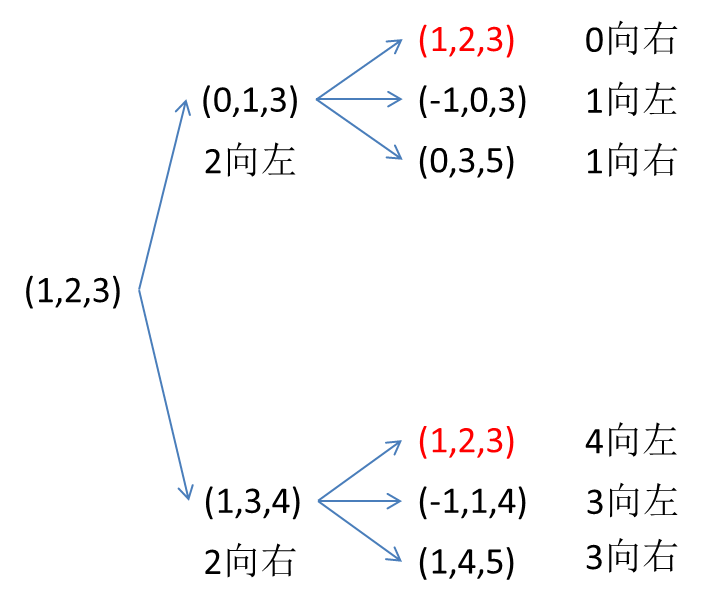
注意红体字部分。
不难发现，当中间数向两边跳时，会产生两种未出现过的子状态，而左右两边数只能取一个距离离中间数小的向中间跳，这样产生的子状态是上一层状态。

看到这里，我们假设把当前状态连条边到子状态，那么就有了

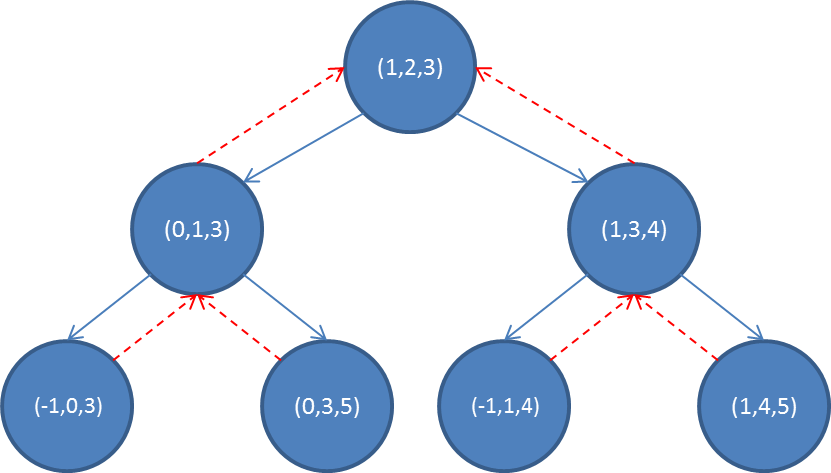
WOC！这不就是一棵树吗？
对吗？完全正确！！

那么最小变化次数不就是求树上两点之间的路径吗？
这不禁又让我们想起。。。LCA！
没错，(dis_{(x,y)}=deep_x+deep_y-2×deep_{LCA(x,y)})

这样我们就有大致的算法框架了。
先求出两个状态的根节点，判断是否相同，若不相同，则直接输出"NO"。
而根节点，其3个数必定构成等差数列，那么我们就存一个公差d和第一个数x，就可以确定了。

但注意一点:
若x,y,z为0,1,10^9，那么我们查找根节点时显然会TLE。
如何优化？
对于上面那组样例，我们可以想成这样

由于这么多次都是z点和x,y之间的距离都不变，也就是说x,y沿着坐标轴平移了一段距离，那么我们就可以快速地算出增加的深度和x,y的最终位置，时间就会大大降低。

至于最后计算路径长度，同样我们可以二分LCA的深度，找到LCA。(类似于倍增算法，若这两个点向上跳跃深度为x时，相等了，就往小的距离去找)

代码:

#include<bits/stdc++.h>
#define int long long
using namespace std;
int st[4],ed[4],dst,ded,lst,led,rtst,rted,ans,last;
void Get(int x,int y,int z,int &deep,int &l,int rt) {
     
    deep=0;
    int d1=y-x,d2=z-y;
    while(d1!=d2) {
        d1=y-x,d2=z-y;
        if(d1<d2) {
            int a1=d2/d1,a2=d2%d1;
            if(a2==0) {
                a1--;
                deep+=a1;
                x+=a1*d1,y+=a1*d1;
                l=d1;
                rt=x;
                return;
            } else {
                deep+=a1;
                x+=a1*d1,y+=a1*d1;
                l=d1;
            }
        } else {
            int a1=d1/d2,a2=d1%d2;
            if(a2==0) {
                a1--;
                deep+=a1;
                z-=a1*d2,y-=a1*d2;
                l=d2;
                rt=x;
                return;
            } else {
                deep+=a1;
                z-=a1*d2,y-=a1*d2;
                l=d2;
            }
        }
    }
    l=d1,rt=x;
    return;
}
void Up(int &x,int &y,int &z,int dep){
    while(dep){
        int d1=y-x,d2=z-y;
        if(d1<d2){
            int a1=d2/d1,a2=d2%d1;
            if(dep<=a1){
                x+=dep*d1,y+=dep*d1;
                return;
            }
            x+=a1*d1,y+=a1*d1;
            dep-=a1;
        }
        else {
            int a1=d1/d2,a2=d1%d2;
            if(dep<=a1){
                y-=dep*d2,z-=dep*d2;
                return;
            }
            z-=a1*d2,y-=a1*d2;
            dep-=a1;
        }
    }
}
signed main() {
    scanf("%lld %lld %lld %lld %lld %lld",&st[1],&st[2],&st[3],&ed[1],&ed[2],&ed[3]);
    sort(st+1,st+4),sort(ed+1,ed+4);
    Get(st[1],st[2],st[3],dst,lst,rtst);
    Get(ed[1],ed[2],ed[3],ded,led,rted);
    //cout<<dst<<" "<<ded;
    if(rtst!=rted||lst!=led){
        puts("NO");
        return 0;
    }
    puts("YES");
    if(dst>ded){
        ans+=dst-ded;
        dst=ded;
        Up(st[1],st[2],st[3],ans);
    }
    else {
        ans+=ded-dst;
        ded=dst;
        Up(ed[1],ed[2],ed[3],ans);
    }
    int l=0,r=dst;
    while(l<=r){
        int mid=(l+r)>>1;
        int a1=st[1],a2=st[2],a3=st[3];
        int b1=ed[1],b2=ed[2],b3=ed[3];
        Up(a1,a2,a3,mid);
        Up(b1,b2,b3,mid);
        if(a1==b1&&a2==b2&&a3==b3){
            last=2*mid;
            r=mid-1;   
        }
        else l=mid+1;
    }
    ans+=last;
    cout<<ans;
    return 0;
}