ZOJ 3806 Incircle and Circumcircle（几何+二分）

博客原文地址：http://blog.csdn.net/xuechelingxiao/article/details/38820755

Incircle and Circumcircle

题目大意：给你一个三角形的内切圆半径跟外接圆半径，求解出符合条件的三角形，输出三角形的三条边的长度，如果没有符合条件的三角形，输出“NO Solution!”。

解题思路：这个题是SP,既是因为情况不唯一，而且还有精度的误差。

　　首先能够想到的就是NO Solution!的情况，即当内切圆半径等于1/2外接圆半径时，此时内切圆最大，而三角形为等边三角形，如图。

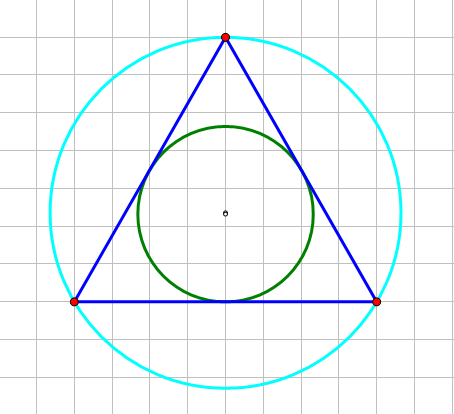
　　其次要解决的就是怎么构造三角形的问题，因为解不唯一，所以只要列举出一种解就OK，于是就很容易的想到构造等腰三角形，在最大与最小之间二分等腰三角形的底边长度，解三角形得到答案，如图。

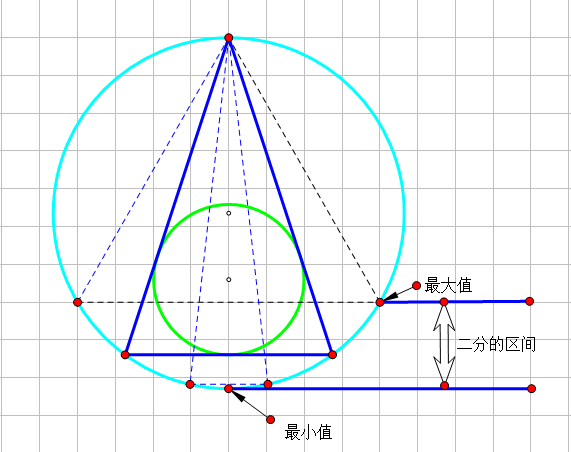
如果还是不明白就看一下代码：

#define sqr(x) (x)*(x)

int main()
{
    double r, R;
    while(~scanf("%lf%lf", &r, &R)){
        if(R < 2*r){
            printf("NO Solution!
");
            continue;
        }
        double left = 0, right = sqrt(3.0)*R;
        while(right-left > eps){
            double mid = (left+right)/2.0;
            double t = sqrt(sqr(sqrt(sqr(R)-sqr(mid/2.0))+R)+sqr(mid/2.0));
            //printf("%lf
", t);
            if(sqr(sqrt(sqr(r)+sqr(t-mid/2.0))+r) + sqr(mid/2.0) - sqr(t) < eps){
                right = mid;
            }
            else {
                left = mid;
            }
        }

        double p = sqrt(sqr(sqrt(sqr(R)-sqr(left/2.0))+R)+sqr(left/2.0));
        printf("%.16lf %.16lf %.16lf
", p, p, left);
    }


    return 0;
}

/*Sample test*/
/*

*/