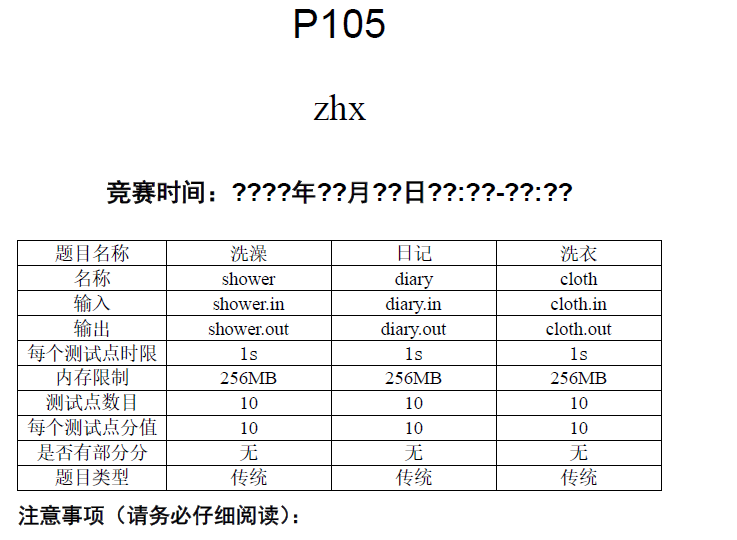
T1 洗澡


贪心:将未匹配的右括号花费1变为左括号,最有多余的左括号有一半变成右括号

1 #include <cstring> 2 #include <cstdio> 3 4 const int N(100005); 5 int n,top,ans; 6 char s[N]; 7 8 int Presist() 9 { 10 freopen("shower.in","r",stdin); 11 freopen("shower.out","w",stdout); 12 scanf("%s",s); n=strlen(s); 13 for(int i=0; i<n; ++i) 14 { 15 if(s[i]=='(') top++; 16 else 17 { 18 if(top<1) top++,ans++; 19 else top--; 20 } 21 } 22 printf("%d ",ans+top/2); 23 return 0; 24 } 25 26 int Aptal=Presist(); 27 int main(int argc,char*argv[]){;}
T2 日记


线性筛出1e6内的所有素数,一共78000++个,对于每次询问暴力查找(可二分)符合条件的最大数,1.6*10^8

1 #include <cstdio> 2 3 inline void read(int &x) 4 { 5 x=0; register char ch=getchar(); 6 for(; ch>'9'||ch<'0'; ) ch=getchar(); 7 for(; ch>='0'&&ch<='9'; ch=getchar()) x=x*10+ch-'0'; 8 } 9 const int N(1e6+5); 10 bool not_pri[N],flag; 11 long long sum[N]; 12 int pri[N],cnt,t; 13 14 inline void Prepare() 15 { 16 register int i,j; 17 for(i=2; i<=1e6; ++i) 18 { 19 if(!not_pri[i]) pri[++cnt]=i; 20 for(j=1; j<=cnt; ++j) 21 { 22 if(i*pri[j]>1e6) break; 23 not_pri[i*pri[j]]=1; 24 if(i%pri[j]==0) break; 25 } 26 } 27 for(i=1; i<=cnt; ++i) 28 sum[i]=sum[i-1]+1ll*pri[i]; 29 } 30 31 int Presist() 32 { 33 freopen("diary.in","r",stdin); 34 freopen("diary.out","w",stdout); 35 // freopen("1.txt","r",stdin); 36 Prepare(); read(t); 37 for(register int n,k,i,j; t--; ) 38 { 39 read(n),read(k); flag=1; 40 for(i=cnt; i>=k; --i) 41 { 42 j=i-k; 43 if(sum[i]-sum[j]<=n) 44 { 45 printf("%I64d ",sum[i]-sum[j]); 46 flag=0; break; 47 } 48 } 49 if(flag) puts("-1"); 50 } 51 return 0; 52 } 53 54 int Aptal=Presist(); 55 int main(int argc,char**argv){;}
T3 洗衣



用f(i)表示第i棵树的值的话,会发现 f(i)=f(i-1)+f(i-2)+一坨奇怪的东西
这坨奇怪的东西大概是某棵树中到某个点的距离之和的几个组合方式,
所以你会发现本质问题实际上需要求第i棵树中所有点到第j个点的距离之和
用g[i][j]表示这个东西,那么我们实际上要想办法求g[i][j],那么这个递归的往下用记忆化搜索的方式历来求

1 #include <algorithm> 2 #include <cstdio> 3 #include <map> 4 5 #define LL long long 6 7 const int mod(1e9+7); 8 const int N(66); 9 10 typedef std:: map<std:: pair<LL,LL>, LL> Mm1; 11 typedef std:: map<LL,LL> Mm2; 12 Mm1 mm1[N]; 13 Mm2 mm2[N]; 14 15 inline void read(LL &x) 16 { 17 x=0; register char ch=getchar(); 18 for(; ch>'9'||ch<'0'; ) ch=getchar(); 19 for(; ch>='0'&&ch<='9'; ch=getchar()) x=x*10+ch-'0'; 20 } 21 22 LL a[N],b[N],c[N],d[N],l[N]; 23 LL F[N],n[N]; 24 25 inline LL dis(LL i,LL x,LL y) 26 { 27 if(x>y) { LL a=x;x=y;y=a;} 28 if(x==y) return 0; 29 Mm1::iterator it=mm1[i].find(std::make_pair(x,y)); 30 if(it!=mm1[i].end()) return it->second; 31 LL na=n[a[i]]; 32 if(x>=na) return mm1[i][std::make_pair(x,y)]=dis(b[i],x-na,y-na)%mod; 33 else if(y<na) return mm1[i][std::make_pair(x,y)]=dis(a[i],x,y)%mod; 34 else return mm1[i][std::make_pair(x,y)]=(dis(a[i],x,c[i])+dis(b[i],d[i],y-na)+l[i])%mod; 35 } 36 37 inline LL f(LL i,LL j) 38 { 39 if(!i) return 0; 40 Mm2:: iterator it=mm2[i].find(j); 41 if(it != mm2[i].end()) return it->second; 42 LL na=n[a[i]]; 43 if(j<na) return mm2[i][j]= ( f(a[i],j)+n[b[i]]%mod* 44 dis(i,j,d[i]+na)%mod+ 45 f(b[i],d[i])) %mod; 46 else return mm2[i][j]= ( f(b[i],j-na)+n[a[i]]%mod* 47 dis(i,j,c[i]) %mod+ 48 f(a[i],c[i])) %mod; 49 } 50 51 int Presist() 52 { 53 freopen("cloth.in","r",stdin); 54 freopen("cloth.out","w",stdout); 55 int m; scanf("%d",&m); 56 F[0]=0; n[0]=1; 57 for(int i=1; i<=m; ++i) 58 { 59 read(a[i]),read(b[i]),read(c[i]),read(d[i]),read(l[i]); 60 n[i]=n[a[i]]+n[b[i]]; l[i]%=mod; 61 LL na=n[a[i]]%mod, nb=n[b[i]]%mod; 62 printf("%I64d ",F[i]=( F[a[i]]+F[b[i]]+ 63 nb*f(a[i],c[i])%mod+ 64 na*f(b[i],d[i])%mod+ 65 na*nb %mod*l[i]%mod)%mod); 66 } 67 return 0; 68 } 69 70 int Aptal=Presist(); 71 int main(int argc,char**argv){;}
