[bzoj2131]免费的馅饼_树状数组

免费的馅饼 bzoj-2131

题目大意：

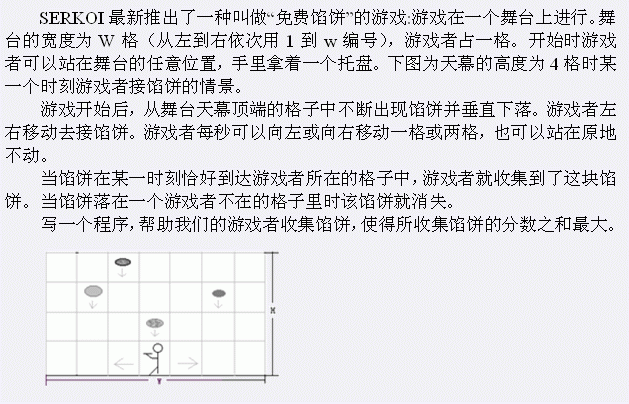
注释：$1le n le 10^5$，$1le w le 10^8$。

想法：首先，想到dp

状态：dp[i][j]表示i分钟在位置j的最大收益

优化优化

状态：dp[i]表示最后收到i的最大收益。

转移：顺序枚举i:1->n即可。

然后，我们尝试优化

对于这个状态我们会发现转移的时候有一个绝对值的死东西，我们将它拆开就有：

2*t[j]+pos[j]<=2*t[i]+pos[i]且2*t[j]-pos[j]<=2*t[i]-pos[i]

然后按照减法为下标，用加法在树状数组上更新即可。

最后，附上丑陋的代码... ...

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int w,n,f[100010],hash[100010],cnt,ans,s[100010];
struct pies
{
	int t,p,v,w1,w2;
}a[100010];
int cmp(const pies &a,const pies &b)
{
	return a.w1<b.w1;
}
int lowbit(int x){return x&(-x);}
int ask(int i)
{
	int Max=0;
	while (i!=0)
	{
		Max=max(Max,s[i]);
		i-=lowbit(i);
	}
	return Max;
}
void add(int i,int val)
{
	while (i<=cnt)
	{
		s[i]=max(s[i],val);
		i+=lowbit(i);
	}
}
int main()
{
	scanf("%d%d",&w,&n);
	for (int i=1;i<=n;i++)
	{
		scanf("%d%d%d",&a[i].t,&a[i].p,&a[i].v);
		a[i].t*=2;
		a[i].w1=a[i].t-a[i].p;
		a[i].w2=a[i].t+a[i].p;
		hash[++cnt]=a[i].w2;
	}
	sort(hash+1,hash+cnt+1);
	cnt=unique(hash+1,hash+cnt+1)-hash-1;
	for (int i=1;i<=n;i++)
	{
		a[i].w2=lower_bound(hash+1,hash+cnt+1,a[i].w2)-hash;
	}
	sort(a+1,a+n+1,cmp);
	for (int i=1;i<=n;i++)
	{
		f[i]=ask(a[i].w2)+a[i].v;
		ans=max(ans,f[i]);
		add(a[i].w2,f[i]);
	}
	printf("%d
",ans);
	return 0;
}

小结：无。