[poj3974]Palindrome_Manacher

Palindrome poj-3974

　　　　题目大意：求字符串的最长回文子串。

　　　　注释：$1le strlen(s) le 10^6$.

　　　　　　想法：介绍一种字符串算法——Manacher。求以每一个字符和字符间隔为回文中心的回文半径长度。什么是Manacher？

　　　　　　　　我们先来考虑这样一种暴力：如果我们用暴力来达到Manacher的效果，我们需要枚举每一个字符以及字符间隔，然后分别向左右扩展更新当前答案，时间复杂度$O(n^2)$，极限数据：连续的同样字符。那么，我们如何对其进行优化？

　　　　

　　　　　　　　我们显然不怎么会处理偶回文子串的方式，那么我们将每两个相邻字符之间加上'#'，来达到只需要求出奇回文子串的效果(很巧妙)。

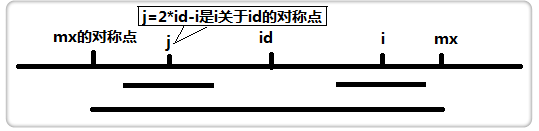
　　　　　　　　紧接着，上面的图表示：

　　　　　　　　　　id为已经处理过的字符串中回文子串最靠右的回文子串的回文中心。无论是字符还是'#'

　　　　　　　　　　mx是id的回文子串右端点。

　　　　　　　　更新... ...

int Manacher()
{
	int maxLen=-1;
	int mx=0;
	int id=0;
	for(int i=0;i<=n;i++)
	{
		if(i<mx)
			p[i]=min(p[2*id-i],mx-i);
		else p[i]=1;
		while(s_new[i-p[i]]==s_new[i+p[i]]) p[i]++;//s_new是带'#'的新字符串
		if(mx<i+p[i])
		{
			id=i;
			mx=i+p[i];
		}
		maxLen=max(maxLen,p[i]-1);
	}
	// for(int i=1;i<=n;i++)
	// {
	// 	cout << i << " " << s_new[i] << " " << p[i] << " " << endl;
	// }
	return maxLen;
}

 　　　　　　显然，是正确的，然后以'#'为回文中心的回文子串就是偶数，反之为奇数。p[i]表示以s_new中的i为回文中心的回文子串的回文半径。

　　　　最后，附上丑陋的代码.. ....

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int n;
int p[2000100];
char s[1000100];
char s_new[2000010];
int Manacher()//Manacher
{
	int maxLen=-1;
	int mx=0;
	int id=0;
	for(int i=0;i<=n;i++)
	{
		if(i<mx)
			p[i]=min(p[2*id-i],mx-i);
		else p[i]=1;
		while(s_new[i-p[i]]==s_new[i+p[i]]) p[i]++;//s_new是带'#'的新字符串
		if(mx<i+p[i])
		{
			id=i;
			mx=i+p[i];
		}
		maxLen=max(maxLen,p[i]-1);
	}
	// for(int i=1;i<=n;i++)
	// {
	// 	cout << i << " " << s_new[i] << " " << p[i] << " " << endl;
	// }
	return maxLen;
}
void original()//初始化
{
	memset(p,0,sizeof p);
	n=0;
}
int main()
{
	int count=0;
	while(1)
	{
		original();
		count++;
		scanf("%s",s+1);
		int k=strlen(s+1);
		if(s[1]=='E') return 0;
		printf("Case %d: ",count);
		s_new[0]='$';//边界小技巧，不用特判
		s_new[++n]='#';
		for(int i=1;i<=k;i++)//建立新字符串
		{
			s_new[++n]=s[i];
			s_new[++n]='#';
		}
		s_new[++n]='!';//+1
		// for(int i=1;i<=k;i++) cout << s[i] ;
		printf("%d
",Manacher());
	}
}

 　　　　小结：Manacher好东西qwq