平面分割问题(jdoj1913)
题目大意:在一维平面内给出n个封闭曲线,保证每两个曲线最多交于两点,求:最多将平面分成多少部分
注释:n<=$10^7$
想法:显然,这是个数学问题,我们自然想到递推处理。博主的方法暴力而优雅...咳咳,打标找规律:$a_i=a_{i-1}+2cdot (i-1)$,下面我们给予证明。首先,先来一张混淆视线的图...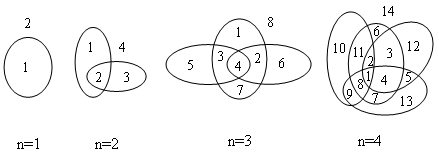 然后,呵呵,发现这图有毒吧,这都是哪跟哪啊,完全看不出规律好不好。其实,这题的关键在于那个极其神奇的条件——每两条曲线只能有两个交点。我们可以进行一波极其强大的打标......
然后,呵呵,发现这图有毒吧,这都是哪跟哪啊,完全看不出规律好不好。其实,这题的关键在于那个极其神奇的条件——每两条曲线只能有两个交点。我们可以进行一波极其强大的打标......
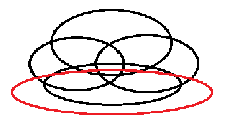 咳咳,查一查,22个。发现这是一个二阶等差数列(这个数列的差是一个等差数列),所以我们我们就做完了啊[无辜qwq]。下面,我们给予证明:
咳咳,查一查,22个。发现这是一个二阶等差数列(这个数列的差是一个等差数列),所以我们我们就做完了啊[无辜qwq]。下面,我们给予证明:
因为有一个条件比较强,(两个交点),所以我们有充分的理由将其简化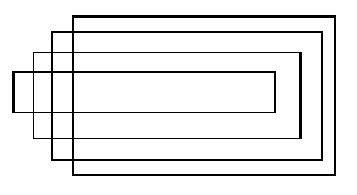 就像这样。所以,每一次我们所增加的矩形,就是像图里的一样,这道题,就完事儿了吗...
就像这样。所以,每一次我们所增加的矩形,就是像图里的一样,这道题,就完事儿了吗...
最后,附上丑陋的代码......
1 #include <iostream> 2 #include <cstdio> 3 typedef long long ll; 4 using namespace std; 5 int main() 6 { 7 ll n; 8 scanf("%lld",&n); 9 printf("%lld",n*n-n+2); 10 return 0; 11 }
错误:想好了就没有错误了嘛,对不对......
这里的图只要出了第一张之外都是博主手画的,扒之前跟我说一声
未经博主允许,严禁转载