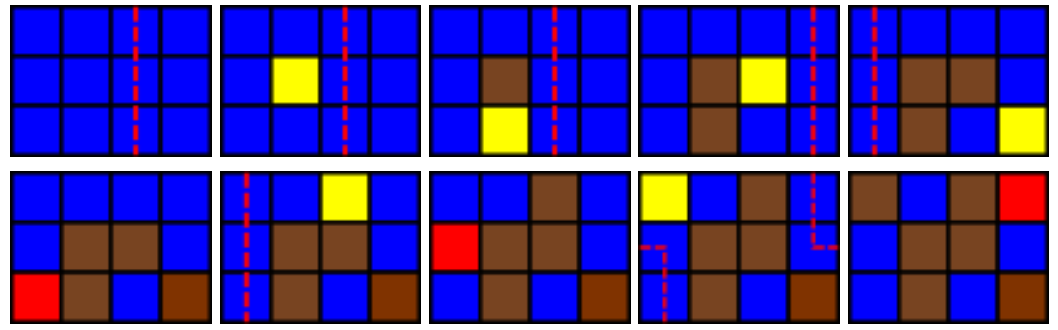
[JZOJ3809] 设备塔
为了封印辉之环,古代塞姆利亚大陆的人民在异空间中建造了一座设备塔。简单的说,这座设备塔是一个漂浮在异空间中的圆柱体,圆柱体两头的圆是计算核心,而侧面则是传输信息所用的数据通道,划分成(N*M)个区块。然而,随着工作的继续进行,他们希望把侧面的一部分区块也改造成其他模块。然而,任何时候都必须保证存在一条数据通道,能从圆柱体的一端通向另一端。由于无法使用辉之环掌控下的计算系统,他们寻求你的帮助来解决这个问题。他们将逐个输入想要改造的区域,而你则执行所有可行的改造并忽略可能导致数据中断的改造。
Input
第一行,包含三个整数(N,M,K),表示侧面的长和宽,以及操作数。接下来(K)行,每行包含两个整数(x_i,y_i),表示操作的区块的坐标。数据保证不会对已经操作成功的区块进行操作。
Output
输出一行,表示有多少个操作可以被执行。
Example
输入 #1
(3) (4) (9)
(2) (2)
(3) (2)
(2) (3)
(3) (4)
(3) (1)
(1) (3)
(2) (1)
(1) (1)
(1) (4)输出 #1
(6)
Explanation
下图显示了改造的每个过程,一共有 6 个改造过程被成功完成。
Scoring
- 对于分值为 30 的子任务 1,保证 (N,M ≤ 100; K ≤ 5000)
- 对于分值为 30 的子任务 2,保证 (N,M ≤ 3000; K ≤ 5000)
- 对于分值为 40 的子任务 3,保证 (N,M ≤ 3000; K ≤ 300000)。
比赛时妹想出来
搞了个暴力18分
普通的加点+判断
//:D
#include<bits/stdc++.h>
using namespace std;
const int dx[3]={0,0,-1},dy[3]={1,-1,0};
int n,m,k,x,y,cnt=0;
bool flag;
int mmap[3010][3010];//map[i][j]==1说明区块已被改造,走不了
bool used[3010][3010];
void dfs(int x,int y)
{
if(x==1){flag=1;return;}//x==1,到达最高点,可以加这个点
for(int i=0;i<3;i++)
{
int nx=x+dx[i];
int ny=y+dy[i];
if(nx<1 || nx>n)return;
if(ny<1)ny=n;if(ny>n)ny=1;//是个环——
if(mmap[nx][ny] || used[nx][ny])continue;//判断——
used[nx][ny]=1;
dfs(nx,ny);//深搜——
used[nx][ny]=0;
if(flag)return;
}
}
int main()
{
//freopen("tower.in","r",stdin);
//freopen("tower.out","w",stdout);
scanf("%d %d %d",&n,&m,&k);
for(int i=1;i<=k;i++)
{
scanf("%d %d",&x,&y);
mmap[x][y]=1;//加点
flag=0;
for(int i=1;i<=m;i++)if(mmap[n][i]==0)dfs(n,i);//枚举最下面一排,没有被改造就深搜往上走
//上面↑这里还可以有个小优化比赛时候居然没加
if(flag)cnt++;//可行方案数++
else mmap[x][y]=0;
}
printf("%d",cnt);
return 0;
}
来看正解——
分析样例
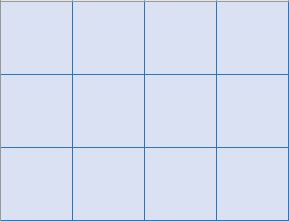
首先这是一个环(废话),所以我们把它复制一遍粘到右边
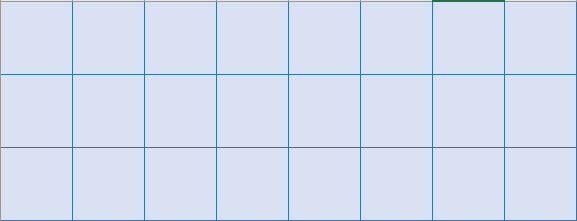
然后来加点。
这个圆柱体上下联通的判定是修改后的模块不会连成一圈,所以加点的时候在原来的地方和我们复制出来的地方都更改一下,然后判定这两个新加的点会不会连起来就好了——
第一个点

第二个点

第三个点
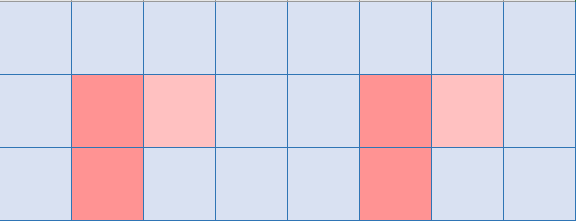
第四个点

第五个点
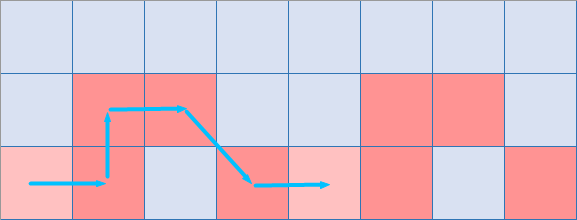
这时候可以看到这两个新加的点连起来了,说明这个时候妹得上下连通的路径,所以不要这个点
第六个点
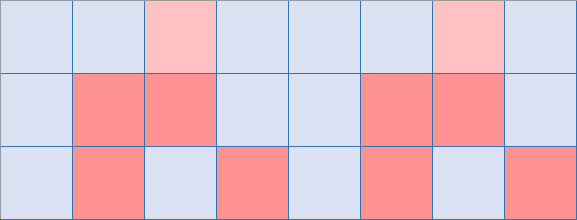
第七个点
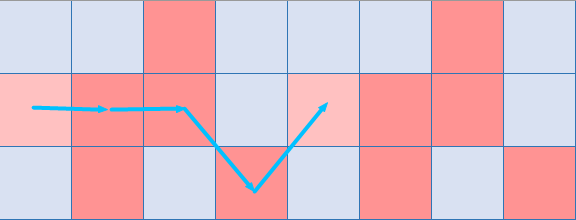
可以看到这俩点又连起来了,撤销
第八个点

第九个点
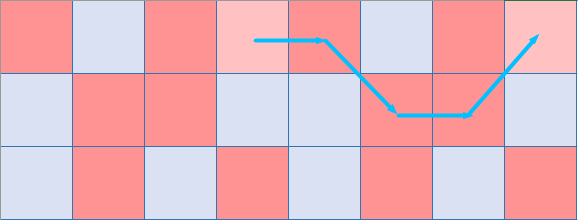
双连起来了,撤销
然后这样就做完啦,数一数没被撤销的有6个点,就是ans
那么有同学就要问了,咋看它们俩有没有连起来呢?
并查集——
上代码上代码
//:D
#include<bits/stdc++.h>
using namespace std;
const int dx[8] = {-1, -1, -1, 0, 0, 1, 1, 1};
const int dy[8] = {-1, 0, 1, -1, 1, -1, 0, 1};//因为连通路线只能上下左右,所以非连通的就要有八个方向
int n, m, k;
int x, y, ans;//ans同时也是一个cnt,用于给加入并查集的点一个序号
int a[3005][6005], fa[6000000+5];//a[i][j]==0说明这个点还没有
int findfa(int x) {//找爸爸
if (fa[x] == x) return x;
fa[x] = findfa(fa[x]);
return fa[x];
}
void connect(int x, int y) {//把点x和点y连到一起
int fax = findfa(x), fay = findfa(y);
if(fax < fay) fa[fay] = fax;
else if(fax > fay) fa[fax] = fay;
}
bool pd(int x, int &y)//pd==1 => 妹有越界 + 已经放到并查集里了
{
if (x <1 || x > n)return 0;//越界
if (y < 1) y = 2 * m;
if (y > 2 * m) y = 1;//skr环
if (!a[x][y])return 0;
return 1;
}
bool judge(int x, int y)
{
int x2 = x, y2 = y + m;//我们复制出来的那个点
for (int i = 0; i < 8; i++)
{
int nx = x + dx[i], ny = y + dy[i];
if (!pd(nx, ny)) continue;
for (int j = 0; j < 8; j++)
{
int nx2 = x2 + dx[j], ny2 = y2 + dy[j];
if (!pd(nx2, ny2)) continue;
if (findfa(a[nx][ny]) == findfa(a[nx2][ny2]))return 0;
//这两个点的周围任意两个点连起来就说明这两个点也会连起来
}
}
return 1;
}
void work(int x, int y) {
a[x][y] = ++ans;
fa[ans] = ans;//它被放到并查集里
for (int i = 0; i < 8; i++) {
int nx = x + dx[i], ny = y + dy[i];
if (!pd(nx, ny)) continue;
connect(a[x][y], a[nx][ny]);//把这个点和周围一圈8个连起来
}
}
int main() {
scanf("%d %d %d", &n, &m, &k);
for (int i = 1; i <= k; i++)
{
scanf("%d %d", &x, &y);
if (judge(x, y))//放入(x,y)后依旧有上下的通路
work(x, y);
work(x, y + m);
}
printf("%d
", ans / 2);//在点(x,y)与(x,y+m)中ans各加了一遍
return 0;
}
后记:
图是用excel做的,第一次做没注意细节导致左边与上面的框截不出来不太美观,第二张图有多截的但我懒得改了
截图好累啊,这我妹想到的