A. Payment Without Change
You have aa coins of value nn and bb coins of value 11. You always pay in exact change, so you want to know if there exist such xx and yy that if you take xx (0≤x≤a0≤x≤a) coins of value nn and yy (0≤y≤b0≤y≤b) coins of value 11, then the total value of taken coins will be SS.
You have to answer qq independent test cases.
The first line of the input contains one integer qq (1≤q≤1041≤q≤104) — the number of test cases. Then qq test cases follow.
The only line of the test case contains four integers aa, bb, nn and SS (1≤a,b,n,S≤1091≤a,b,n,S≤109) — the number of coins of value nn, the number of coins of value 11, the value nn and the required total value.
For the ii-th test case print the answer on it — YES (without quotes) if there exist such xx and yy that if you take xx coins of value nn and yycoins of value 11, then the total value of taken coins will be SS, and NO otherwise.
You may print every letter in any case you want (so, for example, the strings yEs, yes, Yes and YES will all be recognized as positive answer).
4
1 2 3 4
1 2 3 6
5 2 6 27
3 3 5 18
YES NO NO YES
#include <bits/stdc++.h>
using namespace std;
#define ll long long
ll n,m,k,ans,cnt,t;
int main()
{
cin>>t;
while(t--)
{
cin>>n>>m>>ans>>cnt;
ll l = n*ans+m;
if(l<cnt)
cout<<"NO"<<endl;
else
{
if( cnt/ans < n )
{
if( cnt-cnt/ans*ans<=m ) cout<<"YES"<<endl;
else cout<<"NO"<<endl;
}
else
{
if( cnt-n*ans<=m ) cout<<"YES"<<endl;
else cout<<"NO"<<endl;
}
}
}
return 0;
}
B. Minimize the Permutation
#include<bits/stdc++.h>
using namespace std;
const int mxn = 1e2+5;
int vis[mxn],n,arr[mxn],m,cnt,ans,t,k;
int main()
{
cin>>t;
while(t--)
{
cin>>n;
memset(vis,0,sizeof(vis));
for(int i=1;i<=n;i++)
cin>>arr[i];
for(int i=1;i<=n;i++)
{
for(int j=n;j>1;j--)
{
if(arr[j]<arr[j-1] && !vis[j-1])
swap(arr[j],arr[j-1]),vis[j-1] = 1;
}
}
for(int i=1;i<=n;i++)
cout<<arr[i]<<" ";
cout<<endl;
}
return 0;
}
C. Platforms Jumping
There is a river of width nn. The left bank of the river is cell 00 and the right bank is cell n+1n+1 (more formally, the river can be represented as a sequence of n+2n+2 cells numbered from 00 to n+1n+1). There are also mm wooden platforms on a river, the ii-th platform has length cici (so the ii-th platform takes cici consecutive cells of the river). It is guaranteed that the sum of lengths of platforms does not exceed nn.
You are standing at 00 and want to reach n+1n+1 somehow. If you are standing at the position xx, you can jump to any position in the range [x+1;x+d][x+1;x+d]. However you don't really like the water so you can jump only to such cells that belong to some wooden platform. For example, if d=1d=1, you can jump only to the next position (if it belongs to the wooden platform). You can assume that cells 00 and n+1n+1belong to wooden platforms.
You want to know if it is possible to reach n+1n+1 from 00 if you can move any platform to the left or to the right arbitrary number of times (possibly, zero) as long as they do not intersect each other (but two platforms can touch each other). It also means that you cannot change the relative order of platforms.
Note that you should move platforms until you start jumping (in other words, you first move the platforms and then start jumping).
For example, if n=7n=7, m=3m=3, d=2d=2 and c=[1,2,1]c=[1,2,1], then one of the ways to reach 88 from 00 is follow:
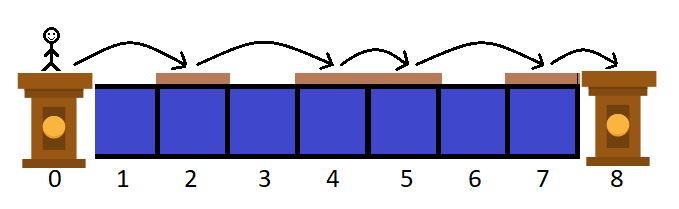The first example: n=7n=7.The first line of the input contains three integers nn, mm and dd (1≤n,m,d≤1000,m≤n1≤n,m,d≤1000,m≤n) — the width of the river, the number of platforms and the maximum distance of your jump, correspondingly.
The second line of the input contains mm integers c1,c2,…,cmc1,c2,…,cm (1≤ci≤n,∑i=1mci≤n1≤ci≤n,∑i=1mci≤n), where cici is the length of the ii-th platform.
If it is impossible to reach n+1n+1 from 00, print NO in the first line. Otherwise, print YES in the first line and the array aa of length nn in the second line — the sequence of river cells (excluding cell 00 and cell n+1n+1).
If the cell ii does not belong to any platform, aiai should be 00. Otherwise, it should be equal to the index of the platform (11-indexed, platforms are numbered from 11 to mm in order of input) to which the cell ii belongs.
Note that all aiai equal to 11 should form a contiguous subsegment of the array aa of length c1c1, all aiai equal to 22 should form a contiguous subsegment of the array aa of length c2c2, ..., all aiai equal to mm should form a contiguous subsegment of the array aa of length cmcm. The leftmost position of 22 in aa should be greater than the rightmost position of 11, the leftmost position of 33 in aa should be greater than the rightmost position of 22, ..., the leftmost position of mm in aa should be greater than the rightmost position of m−1m−1.
See example outputs for better understanding.
7 3 2
1 2 1
YES
0 1 0 2 2 0 3
10 1 11
1
YES
0 0 0 0 0 0 0 0 0 1
10 1 5
2
YES
0 0 0 0 1 1 0 0 0 0
Consider the first example: the answer is [0,1,0,2,2,0,3][0,1,0,2,2,0,3]. The sequence of jumps you perform is 0→2→4→5→7→80→2→4→5→7→8.
Consider the second example: it does not matter how to place the platform because you always can jump from 00 to 1111.
Consider the third example: the answer is [0,0,0,0,1,1,0,0,0,0][0,0,0,0,1,1,0,0,0,0]. The sequence of jumps you perform is 0→5→6→110→5→6→11.
#include <bits/stdc++.h>
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <string>
#include <cstring>
#include <cstdlib>
#include <map>
#include <vector>
#include <set>
#include <queue>
#include <stack>
#include <cmath>
using namespace std;
#define mem(s,t) memset(s,t,sizeof(s))
#define pq priority_queue
#define pb push_back
#define fi first
#define se second
#define ac return 0;
#define ll long long
#define cin2(a,n,m) for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) cin>>a[i][j];
#define rep_(n,m) for(int i=1;i<=n;i++) for(int j=1;j<=m;j++)
#define rep(n) for(int i=1;i<=n;i++)
#define test(xxx) cout<<" Test " <<" "<<xxx<<endl;
#define TLE std::ios::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL); cout.precision(10);
#define lc now<<1
#define rc now<<1|1
#define ls now<<1,l,mid
#define rs now<<1|1,mid+1,r
#define half no[now].l+((no[now].r-no[now].l)>>1)
#define ll long long
const int mxn = 1e6+5;
ll n,m,k,ans,cnt,col;
int a[mxn];
int main()
{
while(cin>>n>>m>>k)
{
ans = 0;
for(int i=1;i<=m;i++)
{
cin>>a[i];
ans+=a[i];
}
if(k==1)
{
if(ans==n)
{
cout<<"YES"<<endl;
for(int i=1;i<=m;i++)
{
while(a[i])
{
cout<<i<<" ";
a[i]--;
}
}
cout<<endl;
}
else
cout<<"NO"<<endl;
}
else if(ans+(k-1)*(m+1)<n)
cout<<"NO"<<endl;
else
{
cnt = n-ans;
cout<<"YES"<<endl;
for(int i=1;i<=m;i++)
{
for(int i=1;i<k && cnt;i++)
{
cout<<0<<" ";
cnt--;
}
for(int j=1;j<=a[i];j++)
{
while( a[i] )
{
cout<<i<<" ";
ans--;
a[i]--;
}
}
}
for(int i=1;i<=cnt;i++)
cout<<0<<" ";
cout<<endl;
}
}
return 0;
}
D. Binary String Minimizing