行列式
主要是行列式的相关计算及结论。
余子式相关的定义比较重要。
矩阵运算
矩阵的乘法中应注意的问题
- 存在非零零因子(即\(AB=0\),而\(A\)和\(B\)均不为\(O\)矩阵)
- 不可交换
- 乘法消去律不成立
- 一些代数恒等式对矩阵不再成立
若可交换,则代数恒等式对矩阵也成立;若\(A\)可逆,则消去律(消去\(A\))也成立。
分块矩阵的乘法规则
- \(A\),\(B\)均按行进行分块
- \(A\)按列分块,\(B\)不分块
- 将\(A\)视作一块,\(B\)按列分块
- 将相关矩阵分成四块
例:证明:上三角矩阵的乘积仍是上三角矩阵
线性方程组
主要涉及到的是方程组的求解。
- 对于非齐次线性方程组:基础解系=特解+通解
- 对于齐次线性方程组:基础解系=通解
求矩阵特解和通解的方法: 满足秩以外的叫自由向量,自由向量都取0用来求特解,自由变量轮流取1,其他的自由变量取0用来求通解。(满足秩的意思即极大无关组)
向量组的极大无关组及秩
矩阵的秩及等价标准形
- 矩阵的秩
这里主要需要注意的是一些常用不等式。

幂等矩阵: 平方等于自身的矩阵。
- 等价标准形

满秩分解
步骤:
- 求极大线性无关组(行变换化成行最简形矩阵)
- 将其余向量用极大线性无关组线性表示
- 拼成两个同秩矩阵相乘
个人理解: 拆分为极大线性无关组和另一个矩阵的乘积即可。
- 一个例子:
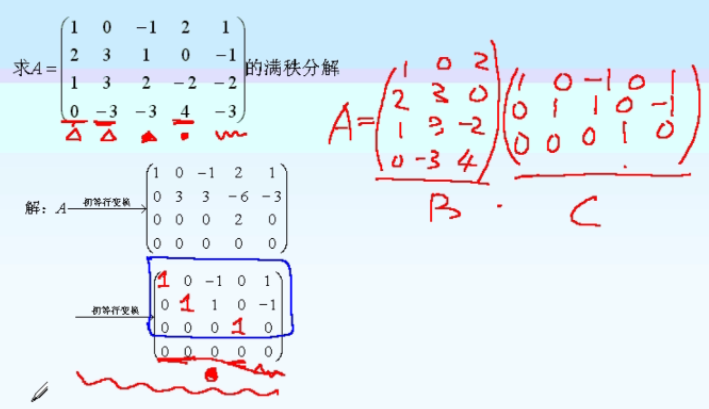
其实与极大线性无关组相乘的那个矩阵并不用求,只要行最简形化对了,C就是蓝色框里的那部分。