牛顿迭代法 求方程根

牛顿迭代法

 

 

牛顿迭代法（Newton's method）又称为牛顿-拉夫逊方法（Newton-Raphson method），它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。多数方程不存在求根公式，因此求精确根非常困难，甚至不可能，从而寻找方程的近似根就显得特别重要。

方法使用函数f(x）的泰勒级数的前面几项来寻找方程f(x) = 0的根。牛顿迭代法是求方程根的重要方法之一，其最大优点是在方程f(x) = 0的单根附近具有平方收敛，而且该法还可以用来求方程的重根、复根，此时线性收敛，但是可通过一些方法变成超线性收敛。另外该方法广泛用于计算机编程中。

计算公式

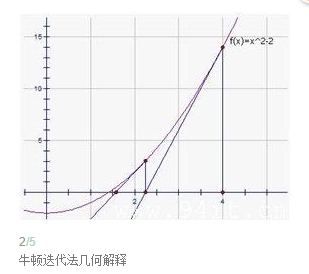
设r是f(x) = 0的根，选取x0作为r初始近似值，过点（x0,f(x0））做曲线y = f(x）的切线L，L的方程为y = f(x0)+f'(x0)(x-x0），求出L与x轴交点的横坐标 x1 = x0-f(x0)/f'(x0），称x1为r的一次近似值。过点（x1,f(x1））做曲线y = f(x）的切线，并求该切线与x轴交点的横坐标 x2 = x1-f(x1）/f'(x1），称x2为r的二次近似值。重复以上过程，得r的近似值序列，其中x(n+1）=x(n）－f(x(n))/f'(x(n)），称为r的n+1次近似值，上式称为牛顿迭代公式。

解非线性方程f(x)=0的牛顿法是把非线性方程线性化的一种近似方法。把f(x）在x0点附近展开成泰勒级数 f(x) = f(x0)+(x－x0)f'(x0)+(x－x0)^2*f''(x0)/2! +… 取其线性部分，作为非线性方程f(x) = 0的近似方程，即泰勒展开的前两项，则有f(x0)+f'(x0)(x－x0)=0 设f'(x0）≠0则其解为x1=x0－f(x0)/f'(x0) 这样，得到牛顿法的一个迭代序列：x(n+1）=x(n）－f(x(n))/f'(x(n)）。

已经证明，如果是连续的，并且待求的零点是孤立的，那么在零点周围存在一个区域，只要初始值位于这个邻近区域内，那么牛顿法必定收敛。 并且，如果不为0, 那么牛顿法将具有平方收敛的性能. 粗略的说，这意味着每迭代一次，牛顿法结果的有效数字将增加一倍。

例题：华为OJ

求解立方根

题目描述

•计算一个数字的立方根，不使用库函数

详细描述：

•接口说明

原型：

public static double getCubeRoot(double input)

输入:double 待求解参数

返回值:double  输入参数的立方根

输入描述:

待求解参数 double类型

输出描述:

输入参数的立方根 也是double类型

输入例子:

216

输出例子:

6.0

#include "iostream"
#include "string"
#include "vector"
#include "algorithm"
#define E 0.005

using namespace std;

double getCubeRoot(double num)
{
    double x0, x1;
    x0 = num;
    x1 = x0 - (x0*x0*x0 - num) / (2 * x0*x0);
    while (x1 - x0 > E || x1 - x0 < -E)
    {
        x0 = x1;
        x1 = x0 - (x0*x0*x0 - num) / (2 * x0*x0);

    }
    return x1;

}

int main()
{
    double n;
    cin >> n;
    cout<<getCubeRoot(n);

}