Luogu-P3807 【模板】卢卡斯定理

题目

题目链接

测试得分：　　100

 

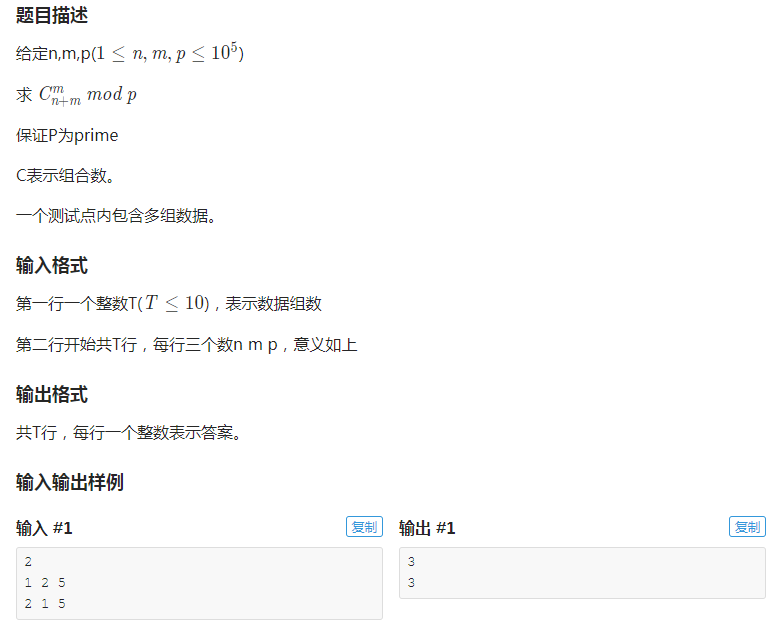
主要算法 ：　　Lucas定理，组合数，逆元

题干：

　　　Lucas板子

分析

　　运用Lucas定理

　　　　

　　代码

 　　

#include<stdio.h>
#include<stdlib.h>
#define FORa(i,s,e) for(int i=s;i<=e;i++)
#define FORs(i,s,e) for(int i=s;i>=e;i--)
#define gc pa==pb&&(pb=(pa=buf)+fread(buf,1,100000,stdin),stdin)?EOF:*pa++

using namespace std;
char buf[100000],*pa,*pb;
inline int read();

const int N=1e5;
int k,n,m,p;
long long a[N+1],b[N+1];
long long Lucas(int x,int y)
{
    if(x<y) return 0;
    else if(x<p) return b[x]*a[y]*a[x-y]%p;
    else return Lucas(x/p,y/p)*Lucas(x%p,y%p)%p;
}
int main()
{
    k=read();
    while(k--)
    {
        n=read(),m=read(),p=read(); 
        a[0]=a[1]=b[0]=b[1]=1;
        FORa(i,2,n+m) b[i]=b[i-1]*i%p;//计算阶乘 
        FORa(i,2,n+m) a[i]=(p-p/i)*a[p%i]%p;//线性求逆元 
        FORa(i,2,n+m) a[i]=a[i-1]*a[i]%p;//阶乘逆元 
        printf("%lld
",Lucas(n+m,m));
    }
    return 0;
}
inline int read()
{
    register char c(gc);register int f(1),x(0);
    while(c<'0'||c>'9') f=c=='-'?-1:1,c=gc;
    while(c>='0'&&c<='9') x=(x<<1)+(x<<3)+(c^48),c=gc;
    return x*f;
}

总结：

　　1.预处理出逆元