Tree
Node节点 root树根 degree度 leaf 树叶
level层次 depth深度 forest森林 BT二叉树
树是一种非线性的数据结构,用它能很好地描述有分支和层次特性的数据集合。树型结构在现实世界中广泛存在,如社会组织机构的组织关系图就可以用树型结构来表示。树在计算机领域中也有广泛应用,如在编译系统中,用树表示源程序的语法结构。在数据库系统中,树型结构是数据库层次模型的基础,也是各种索引和目录的主要组织形式。在许多算法中,常用树型结构描述问题的求解过程、所有解的状态和求解的对策等。在这些年的国内、国际信息学奥赛、大学生程序设计比赛等竞赛中,树型结构成为参赛者必备的知识之一,尤其是建立在树型结构基础之上的搜索算法。
在树型结构中,二叉树是最常用的结构,它的分支个数确定、又可以为空、并有良好的递归特性,特别适宜于程序设计,因此也常常将一般树转换成二叉树进行处理。
一棵树是由n(n>0)个元素组成的有限集合,其中:
(1)每个元素称为结点(node);
(2)有一个特定的结点,称为根结点或树根(root);
(3)除根结点外,其余结点能分成m(m>=0)个互不相交的有限集合T0,T1,T2,……Tm-1。其中的每个子集又都是一棵树,这些集合称为这棵树的子树。
如下图是一棵典型的树:
(1)树是递归定义的;
(2)一棵树中至少有1个结点。这个结点就是根结点,它没有前驱,其余每个结点都有唯一的一个前驱结点。每个结点可以有0或多个后继结点。因此树虽然是非线性结构,但也是有序结构。至于前驱后继结点是哪个,还要看树的遍历方法,我们将在后面讨论;
(3)一个结点的子树个数,称为这个结点的度(degree,结点1的度为3,结点3的度为0);度为0的结点称为叶结点(树叶leaf,如结点3、5、6、8、9);度不为0的结点称为分支结点(如结点1、2、4、7);根以外的分支结点又称为内部结点(结点2、4、7);树中各结点的度的最大值称为这棵树的度(这棵树的度为3)。
(4)在用图形表示的树型结构中,对两个用线段(称为树枝)连接的相关联的结点,称上端结点为下端结点的父结点,称下端结点为上端结点的子结点。称同一个父结点的多个子结点为兄弟结点。如结点1是结点2、3、4的父结点,结点 2、3、4是结点1的子结点,它们又是兄弟结点,同时结点2又是结点5、6的父结点。称从根结点到某个子结点所经过的所有结点为这个子结点的祖先。如结点1、4、7是结点8 的祖先。称以某个结点为根的子树中的任一结点都是该结点的子孙。如结点7、8、9都是结点4的子孙。
(5)定义一棵树的根结点的层次(level)为1,其它结点的层次等于它的父结点层次加1。如结点2、3、4的层次为1,结点5、6、7的层次为2,结点8、9的层次为3。一棵树中所有的结点的层次的最大值称为树的深度(depth)。如这棵树的深度为3。
(6)对于树中任意两个不同的结点,如果从一个结点出发,自上而下沿着树中连着结点的线段能到达另一结点,称它们之间存在着一条路径。可用路径所经过的结点序列表示路径,路径的长度等于路径上的结点个数减1。如上图中,结点1和结点8之间存在着一条路径,并可用(1、4、7、8)表示这条路径,该条路径的长度为3。注意,不同子树上的结点之间不存在路径,从根结点出发,到树中的其余结点一定存在着一条路径。
(7)森林(forest)是m(m>=0)棵互不相交的树的集合。
树的存储结构
方法1:数组,称为“父亲表示法”。
const int m = 10; 树的结点数
struct node
{int data, parent;}; 数据域,指针域
node tree[m];
优缺点:利用了树中除根结点外每个结点都有唯一的父结点这个性质。很容易找到树根,但找孩子时需要遍历整个线性表。
方法2:树型单链表结构,称为“孩子表示法”。每个结点包括一个数据域和一个指针域(指向若干子结点)。称为“孩子表示法”。假设树的度为10,树的结点仅存放字符,则这棵树的数据结构定义如下:
const int m = 10; 树的度
typedef struct node;
typedef node *tree;
struct node
{
char data; 数据域
tree child[m]; 指针域,指向若干孩子结点
};
tree t;
缺陷:只能从根(父)结点遍历到子结点,不能从某个子结点返回到它的父结点。但程序中确实需要从某个结点返回到它的父结点时,就需要在结点中多定义一个指针变量存放其父结点的信息。这种结构又叫带逆序的树型结构。
方法3:树型双链表结构,称为“父亲孩子表示法”。每个结点包括一个数据域和二个指针域(一个指向若干子结点,一个指向父结点)。假设树的度为10,树的结点仅存放字符,则这棵树的数据结构定义如下:
const int m = 10; 树的度
typedef struct node;
typedef node *tree; 声明tree是指向node的指针类型
struct node
{
char data; 数据域
tree child[m]; 指针域,指向若干孩子结点
tree father; 指针域,指向父亲结点
};
tree t;
方法4:二叉树型表示法,称为“孩子兄弟表示法”。也是一种双链表结构,但每个结点包括一个数据域和二个指针域(一个指向该结点的第一个孩子结点,一个指向该结点的下一个兄弟结点)。称为“孩子兄弟表示法”。假设树的度为10,树的结点仅存放字符,则这棵树的数据结构定义如下:
typedef struct node;
typedef node *tree;
struct node
{
char data; 数据域
tree firstchild, next;指针域,分别指向第一个孩子结点和下一个兄弟结点
};
tree t;
树的遍历
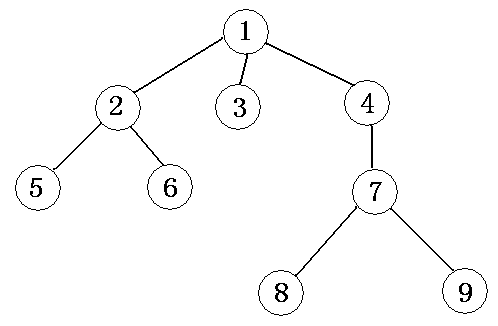
A、先序遍历:根左右
如上图先序遍历的结果为:125634789;
B、中序遍历:左根右
C、后序遍历:左右根
如上图后序遍历的结果为:562389741;
D、层次遍历:
如上图层次遍历的结果为:123456789;
E、叶结点遍历:
如上图按照这个思想访问的结果为:56389;
感谢各位与信奥一本通的鼎力相助!