-
题目介绍:
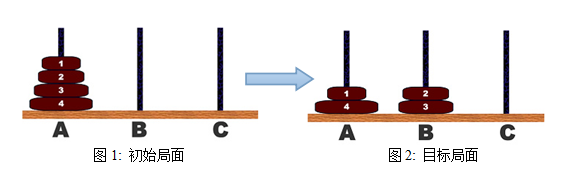
标准的汉诺塔上有n个大小各异的盘子。现给定一个初始局面(见图1),求它到目标局面(见图2)至少需要移动多少步?
移动规则:一次只能移动一个盘子;且在移动盘子之前,必须把压在上面的其他盘子先移走;基于汉诺塔问题的原始约定,编号大的盘子不得压在编号小的盘子上。
Sample Input
3
1 1 1
2 2 2
3
1 2 3
3 2 1
4
1 1 1 1
1 1 1 1
0
Sample Output
Case 1: 7
Case 2: 3
Case 3: 0
-
问题分析:
为了更好的剖析问题。我们首先考虑编号最大的盘子。显然,如果这个盘子的在初始局面和目标局面中位于同一根柱子,那么我们可以根本不需要移动它。直接忽略它在两个局面的存在。
设现在存在初始局面跟目标局面中位置不同的盘子最大编号为k。现在设想一下移动k之前的瞬间。不妨假设盘子k需要从柱子A移动到柱子B,那么在移动k之前的局面必然是,1,2,...k-1全部位于柱子C,而且从上到下排好序。我们把这个局面称为参考局面。
根据对称性,我们只需要求出初始局面和目标局面到参考局面移动的步数之和,再加上1(移动编号为k的盘子)即可。
现定义这样的一个函数 f(arr,k,flag):表示已知各盘子的初始编号为数组arr,把1,2,...,k移动到flag柱子所需要的最少步数。可得本题答案表示如下:
ans = f(start,k-1,6-start[k]-finish[kl) + f(finish,k-1,6-start[k]-finish[kl) + 1;
将问题分解之后,我们再考虑如何基于汉诺塔的性质,递归求解f(arr,k,flag)。
显然,k=0时意味着没有盘子需要移动,此时返回0,作为递归跳出的判断条件;
K!=0时,比较arr[k]==flag? 如果相等,那么很好办,直接f(arr,k,flag) = f(arr,k-1,flag)即可,因为编号k不需要移动。当arr[k]!=flag时就需要推导一下了。我们把“1,2,...,k-1”看做一个整体,此时移动k前后需要将整体从一个柱子移动到另一个柱子,而根据汉诺塔的经典理论,将n个盘子初始有序的盘子由一个柱子移动到另一个柱子最少需要:2^n - 1 次。本题中,我们还要加上移动盘子k的一次操作,故最后:
f(arr,k,flag) = f(arr,k-1,6-arr[k]-flag) + (1<<(k-1))
-
参考代码:
1 #include <cstdio> 2 3 typedef long long ll; 4 5 const int maxn=64; 6 7 int a[maxn],b[maxn]; 8 9 10 11 ll f(int *a,int k,int flag){ 12 13 if(k<1) return 0; 14 15 else if(a[k]==flag){ 16 17 return f(a,k-1,flag); 18 19 }else{ 20 21 return f(a,k-1,6-a[k]-flag) + (1LL<<(k-1)); //"1LL"自动转换为long long 类型 22 23 } 24 25 } 26 27 int main(){ 28 29 int n,t=1; 30 31 while(scanf("%d",&n)==1 && n){ 32 33 for(int i=1;i<=n;i++) scanf("%d",&a[i]); 34 35 for(int i=1;i<=n;i++) scanf("%d",&b[i]); 36 37 38 39 //find 'k' 40 41 int k=n; 42 43 while(a[k]==b[k] && k>=1)k--; 44 45 46 47 ll ans=0; 48 49 ans = f(a,k-1,6-a[k]-b[k]) + f(b,k-1,6-a[k]-b[k]) + 1; 50 51 if(k==0) ans = 0; 52 53 printf("Case %d: %lld ",t++,ans); 54 55 } 56 57 return 0; 58 59 } 60 61
结语:
这道题从刚开始入手的杂乱通过一步步转换推导之后,最终程序的精简实现不由得让人拍案叫绝!本文解析或许词不达意,不到之处请谅解。同时,欢迎有其他思路或想法的朋友私下交流讨论。
(hint:提交本题目时注意数据类型选用64位整型数long long,”(1<<(k-1))”若没有加上“LL”则提交结果为WA! )