题意:

k<=2^20,n<=10^15.
标程:
1 #include<cstdio> 2 using namespace std; 3 typedef long long ll; 4 const int mod=998244353; 5 const int root=31; 6 ll wn,w,ans,l,n,k; 7 ll ksm(ll x,ll y) 8 { 9 ll res=1; 10 while (y) {if (y&1) res=res*x%mod; x=x*x%mod; y>>=1;} 11 return res; 12 } 13 int main() 14 { 15 scanf("%lld%lld",&n,&k); 16 l=31-__builtin_clz(k);w=ksm(root,1<<23-l);wn=1; 17 for (int i=0;i<k;i++) 18 ans=(ans+ksm(1+wn,n))%mod,wn=wn*w%mod; 19 printf("%lld ",ans*ksm(k,mod-2)%mod); 20 return 0; 21 }
题解:二项式定理+原根
当k=1的时候,Ans=sigma(C(n,i))=(1+x)^n=2^n.
当k=2的时候,将x=-1代入,将两个式子加起来/2就是Ans。(1^j+(-1)^j)/2
当k=4的时候……我们可以仿照fft的奇偶分组过程,给每个项一个系数,当k|i,第i项的系数为1。
原根(n次单位根)可以解决!得到如下判定式:
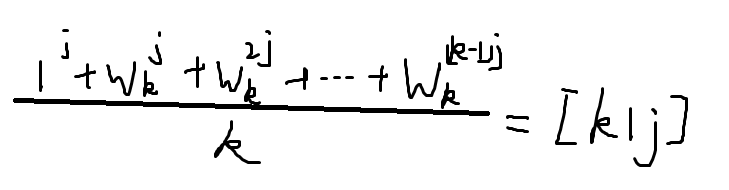
运用对复根的二项式定理可以化简答案式:

O(klogn)。