题意:一个班级n个人,如果a爱b,那么a->b一条有向边。问有多少种删边集合使得图仍然强联通? n<=15.
标程:
1 #include<cstdio> 2 #include<algorithm> 3 #include<cstring> 4 #include<bitset> 5 using namespace std; 6 typedef long long ll; 7 const int mod=1e9+7; 8 const int N=32770; 9 int read() 10 { 11 int x=0,f=1;char ch=getchar(); 12 while (ch<'0'||ch>'9') {if (ch=='-') f=-1;ch=getchar();} 13 while (ch>='0'&&ch<='9') x=(x<<1)+(x<<3)+ch-'0',ch=getchar(); 14 return x*f; 15 } 16 int n,m,Max,pop[N],pow[N],sum_e[N],to_e[N],f[N],a,b,e[N],ie[N],u[N]; 17 int lowbit(int x){return x&(-x);} 18 int main() 19 { 20 n=read();m=read(); 21 for (int i=1;i<=m;i++) 22 { 23 a=read(),b=read(); 24 e[1<<a-1]|=1<<b-1,ie[1<<b-1]|=1<<a-1; 25 } 26 Max=1<<n;pow[0]=1; 27 for (int i=1;i<Max;i++) pop[i]=pop[i>>1]+(i&1),pow[i]=(ll)pow[i-1]*2%mod; 28 for (int i=1;i<Max;i++) 29 { 30 int v=lowbit(i);int p=i^v; 31 sum_e[i]=sum_e[i^v]+pop[e[v]&i]+pop[ie[v]&i]; 32 f[i]=pow[sum_e[i]];to_e[i]=0; 33 for (int j=p;j;j=(j-1)&p) 34 u[i]=((ll)u[i]-(ll)f[i^j]*u[j]%mod+mod)%mod; 35 for (int j=i;j;j=(j-1)&i) 36 { 37 int v=lowbit(i^j);to_e[j]=to_e[j|v]-pop[e[v]&(i^j)]+pop[ie[v]&j]; 38 f[i]=((ll)f[i]-(ll)pow[sum_e[i^j]+to_e[j]]*u[j]%mod+mod)%mod; 39 } 40 u[i]=((ll)u[i]+f[i])%mod; 41 } 42 printf("%d ",f[Max-1]); 43 return 0; 44 }
技巧:用lowbit(i)取出i中的任意一个元素(注意是移位<<后的)。
题解:状压枚举子集+容斥dp
乍一看只知道状压。。。强联通是什么鬼嘛。。。
考虑一个不强联通的图,至少有一个点的入度为0。
这样就可以容斥啦:全集-不强连通的图数=强联通的图数。
枚举缩点后入度为0的块有多少个,设包含入度为0的块的集合为T。f[S]表示S集合中的点构成强联通图的方案数,g[S][k]表示将S集合分成k个独立块的方案数,u[S][k]表示带容斥系数的g之和。e(S)表示S点集中的边数。e(S,T)表示从S中的点连出向T的边数。

u[S]也可以通过容斥求得。为了不算重,取一个S集中的点v作为连通块部分的必选点。(减号就相当于是连通块个数+1,(-1)^k变号)
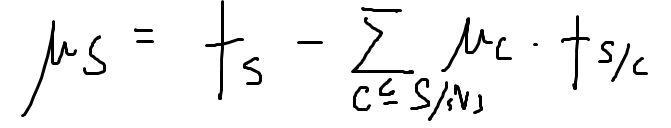
求u和f的时间复杂度都是O(n^3)。求e(S)和e(S,T)都可以通过在子集上累加的方法计算。