彻底搞懂CNN中的卷积和反卷积

                    版权声明：本文为博主原创文章，未经博主允许不得转载。                        https://blog.csdn.net/sinat_29957455/article/details/85558870                    </div>
                                                <link rel="stylesheet" href="https://csdnimg.cn/release/phoenix/template/css/ck_htmledit_views-3019150162.css">
                                    <div id="content_views" class="markdown_views prism-atom-one-dark">
                <!-- flowchart 箭头图标 勿删 -->
                <svg xmlns="http://www.w3.org/2000/svg" style="display: none;">
                    <path stroke-linecap="round" d="M5,0 0,2.5 5,5z" id="raphael-marker-block" style="-webkit-tap-highlight-color: rgba(0, 0, 0, 0);"></path>
                </svg>
                                        <h4><a id="_0"></a>前言</h4>

卷积和反卷积在CNN中经常被用到，想要彻底搞懂并不是那么容易。本文主要分三个部分来讲解卷积和反卷积，分别包括概念、工作过程、代码示例，其中代码实践部分主结合TensorFlow框架来进行实践。给大家介绍一个卷积过程的可视化工具，这个项目是github上面的一个开源项目。

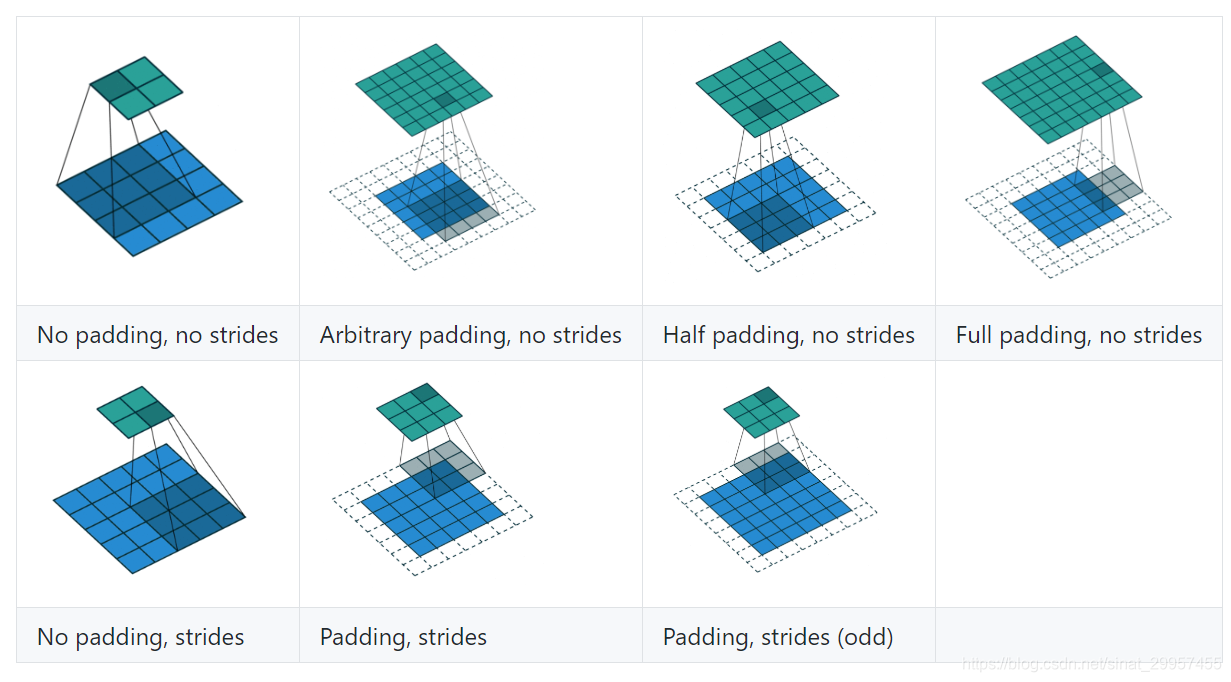
卷积和反卷积

卷积(Convolutional)：卷积在图像处理领域被广泛的应用，像滤波、边缘检测、图片锐化等，都是通过不同的卷积核来实现的。在卷积神经网络中通过卷积操作可以提取图片中的特征，低层的卷积层可以提取到图片的一些边缘、线条、角等特征，高层的卷积能够从低层的卷积层中学到更复杂的特征，从而实现到图片的分类和识别。
反卷积：反卷积也被称为转置卷积，反卷积其实就是卷积的逆过程。大家可能对于反卷积的认识有一个误区，以为通过反卷积就可以获取到经过卷积之前的图片，实际上通过反卷积操作并不能还原出卷积之前的图片，只能还原出卷积之前图片的尺寸。那么到底反卷积有什么作用呢？通过反卷积可以用来可视化卷积的过程，反卷积在GAN等领域中有着大量的应用。

工作过程

卷积

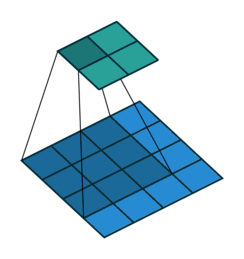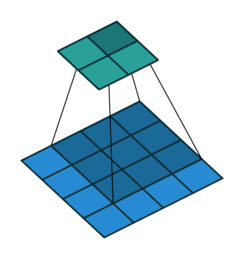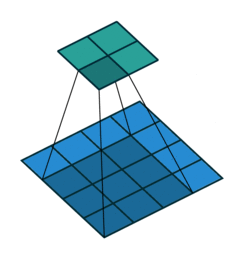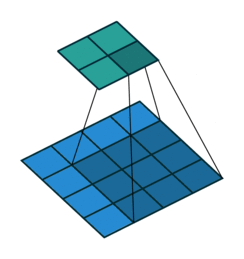
上图展示了一个卷积的过程，其中蓝色的图片(4*4)表示的是进行卷积的图片，阴影的图片(3*3)表示的是卷积核，绿色的图片(2*2)表示是进行卷积计算之后的图片。在卷积操作中有几个比较重要的参数，输入图片的尺寸、步长、卷积核的大小、输出图片的尺寸、填充大小。
下面用一个图来详细介绍这些参数：

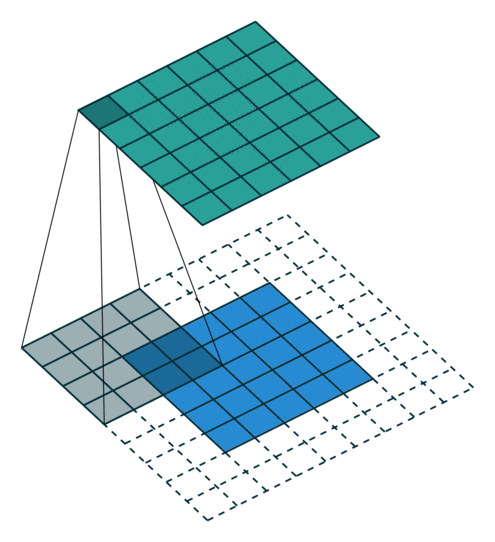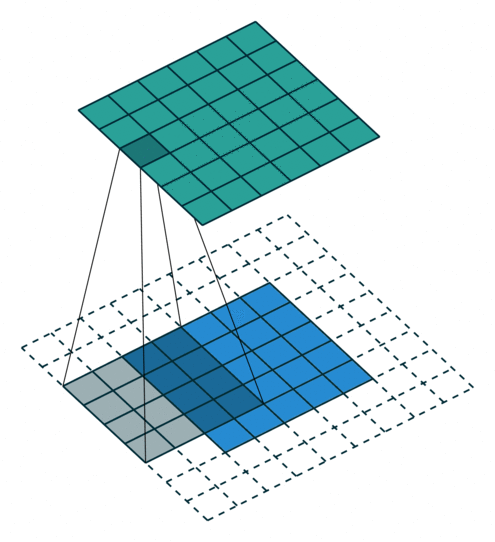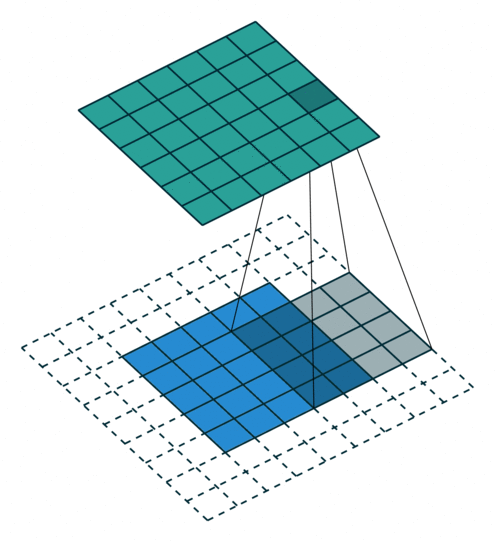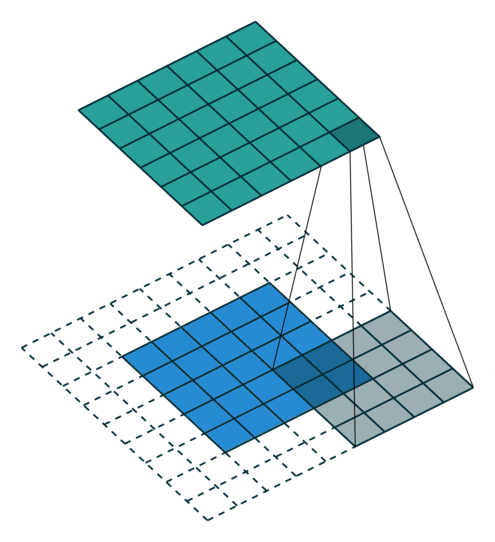
输入图片的尺寸：上图中的蓝色图片(55)，表示的是需要进行卷积操作的图片，在后面的公式中有i$i$i来表示输入图片的尺寸。
卷积核的大小：上图中的会移动阴影图片表示的是卷积核(44)，通过不同参数不同大小的卷积核可以提取到图片的不同特征，后面用k$k$k表示卷积核的尺寸。
步长：是指卷积核移动的长度，通过上图可以发现卷积核水平方向移动的步长和垂直方向移动的步长是一样的都是1，后面用s$s$s表示步长。
填充大小：是指在输入图片周围填充的圈数，通常都是用0来进行填充的，上图中蓝色图片周围两圈虚线的矩形表示的是填充的值，所以填充掉是2，后面用p$p$p来表示填充大小。
输出图片的尺寸：经过卷积操作之后获取到的图片的大小，上图的绿色图片(6*6)，后面用o来表示。
如果已知i、k、p、s$i、k、p、s$i、k、p、s，可以求得o$o$o，计算公式如下：
o=i−k+2∗ps+1$o=frac{i-k+2*p}{s}+1$o=si−k+2∗p​+1

反卷积

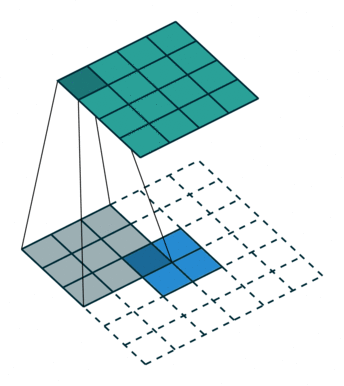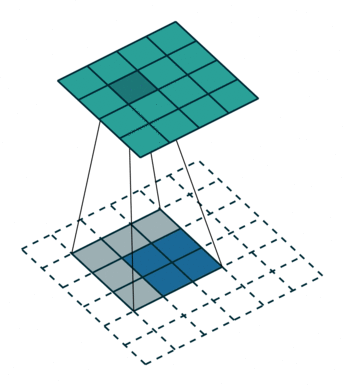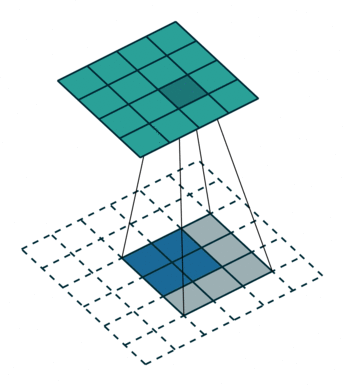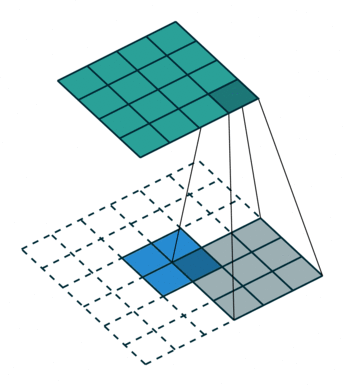
上图展示一个反卷积的工作过程，乍看一下好像反卷积和卷积的工作过程差不多，主要的区别在于反卷积输出图片的尺寸会大于输入图片的尺寸，通过增加padding来实现这一操作，上图展示的是一个strides(步长)为1的反卷积。下面看一个strides不为1的反卷积

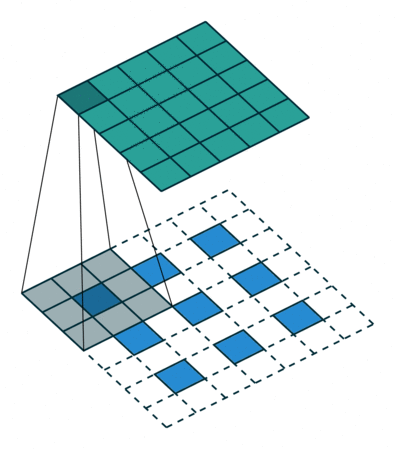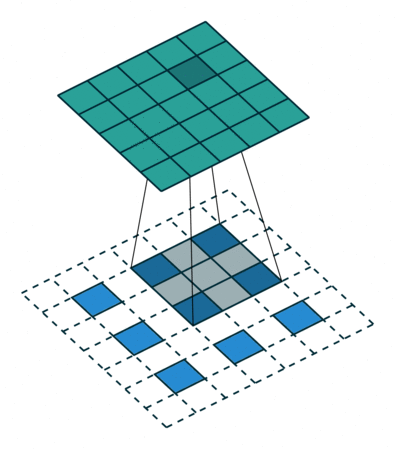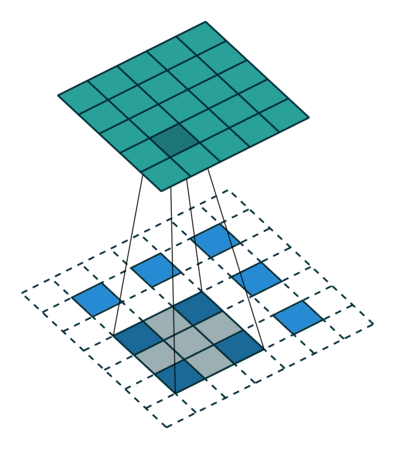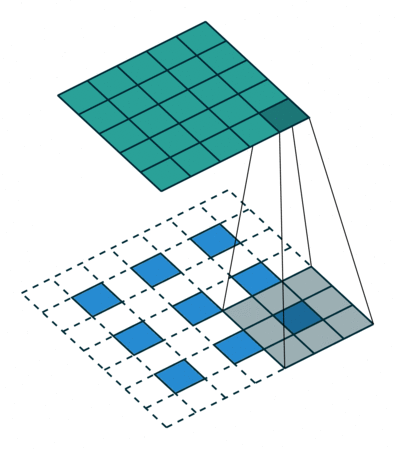
上图中的反卷积的stride为2，通过间隔插入padding来实现的。同样，可以根据反卷积的o、s、k、p$o、s、k、p$o、s、k、p参数来计算反卷积的输出i$i$i，也就是卷积的输入。公式如下：i=(o−1)∗s+k−2∗p$i=(o-1)*s+k-2*p$i=(o−1)∗s+k−2∗p，其实就是根据上式推导出来的。

代码示例

为了便于大家理解卷积和反卷积工作过程，将会使用图示的方式来展示卷积和反卷积的工作过程，并利用tensorflow的卷积和反卷积函数来进行验证。

卷积

使用tensorflow来实现卷积的时候，主要利用tf.nn.conv2d函数来实现的，先介绍一下函数的参数
功能说明：通过4维的input和filter来计算2维卷积

• input：4维的tensor，需要进行卷积的矩阵
• filter：4维的tensor，卷积核的参数，需要和input具有相同的数据类型，[filter_height，filter_width，in_channels，out_channels]，其中filter_height表示卷积核的高，filter_width表示卷积核的宽，in_channels表示需要进行卷积图片的通道数，out_channels卷积之后输出的通道数
• strides：int类型的列表，设置卷积核滑动的步长
• padding：填充类型有"SAME"和"VALID"两种模式，当步长为1时，padding为"SAME"可以保持输出与输入的尺寸具有相同的大小。
• use_cudnn_on_gpu：使用cudnn来加速卷积，默认是True
• data_format：输入数据的格式，有"NHWC"和"NCHW"两种模式，默认使用的是"NHWC"，表示[batch，height，width，channels]，"NCHW"数据格式[batch，channels，height，width]
• dilations：一维的list，默认是[1,1,1,1]，用来设置卷积核的扩展
• name：操作的名称

TensorFlow提供的卷积函数padding只有"SAME"和"VALID"两种模式，所以输出矩阵的尺寸大小与之前的公式有所不同，下面介绍这两种模式下输出矩阵尺寸的计算公式：
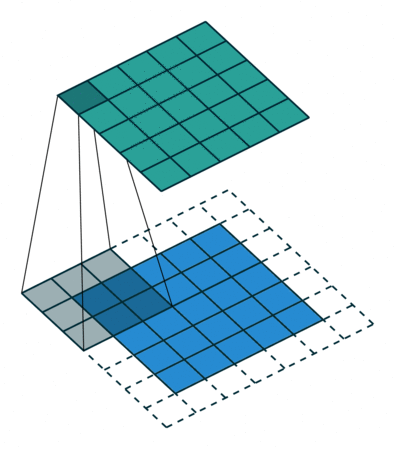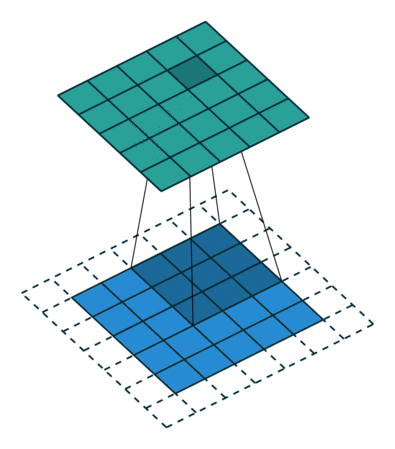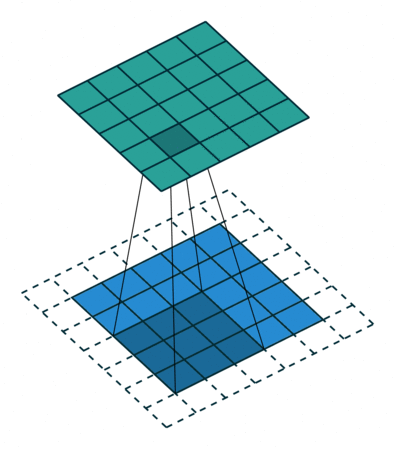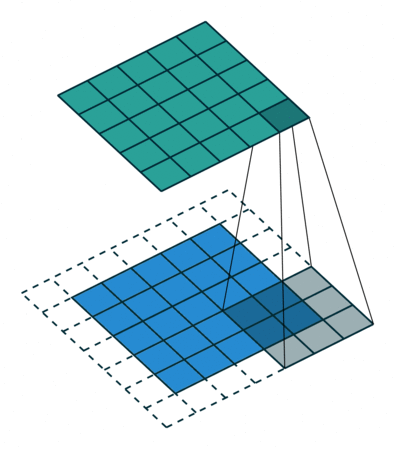
padding为SAME时：ceil(i/s)$ceil(i/s)$ceil(i/s)，其中i$i$i表示输入矩阵的大小，s表示卷积核的步长，ceil函数表示向上取整。下图展示是一个padding为SAME的卷积，卷积开始的时候保证卷积核的中心位于输入矩阵角的顶点位置。

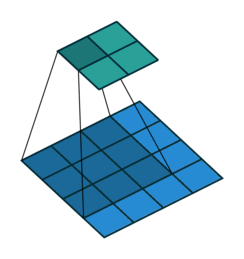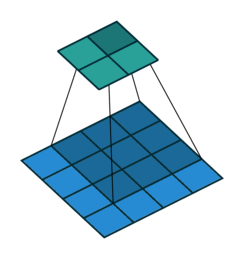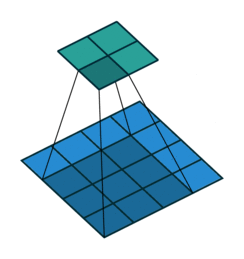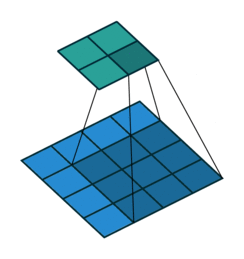
padding为VALID时：ceil((i−k+1)/s)$ceil((i-k+1)/s)$ceil((i−k+1)/s)，k$k$k表示卷积核的尺寸。下图展示的是一个padding为VALID的卷积过程，卷积核始终都是位于输入矩阵内进行移动。

    x1 = tf.constant(1.0, shape=[1,4,4,3])
    x2 = tf.constant(1.0,shape=[1,6,6,3])
    kernel = tf.constant(1.0,shape=[3,3,3,1])
y1_1 <span class="token operator">=</span> tf<span class="token punctuation">.</span>nn<span class="token punctuation">.</span>conv2d<span class="token punctuation">(</span>x1<span class="token punctuation">,</span>kernel<span class="token punctuation">,</span>strides<span class="token operator">=</span><span class="token punctuation">[</span><span class="token number">1</span><span class="token punctuation">,</span><span class="token number">2</span><span class="token punctuation">,</span><span class="token number">2</span><span class="token punctuation">,</span><span class="token number">1</span><span class="token punctuation">]</span><span class="token punctuation">,</span>padding<span class="token operator">=</span><span class="token string">"SAME"</span><span class="token punctuation">)</span>
y1_2 <span class="token operator">=</span> tf<span class="token punctuation">.</span>nn<span class="token punctuation">.</span>conv2d<span class="token punctuation">(</span>x1<span class="token punctuation">,</span>kernel<span class="token punctuation">,</span>strides<span class="token operator">=</span><span class="token punctuation">[</span><span class="token number">1</span><span class="token punctuation">,</span><span class="token number">2</span><span class="token punctuation">,</span><span class="token number">2</span><span class="token punctuation">,</span><span class="token number">1</span><span class="token punctuation">]</span><span class="token punctuation">,</span>padding<span class="token operator">=</span><span class="token string">"VALID"</span><span class="token punctuation">)</span>
y2_1 <span class="token operator">=</span> tf<span class="token punctuation">.</span>nn<span class="token punctuation">.</span>conv2d<span class="token punctuation">(</span>x2<span class="token punctuation">,</span>kernel<span class="token punctuation">,</span>strides<span class="token operator">=</span><span class="token punctuation">[</span><span class="token number">1</span><span class="token punctuation">,</span><span class="token number">2</span><span class="token punctuation">,</span><span class="token number">2</span><span class="token punctuation">,</span><span class="token number">1</span><span class="token punctuation">]</span><span class="token punctuation">,</span>padding<span class="token operator">=</span><span class="token string">"SAME"</span><span class="token punctuation">)</span>
y2_2 <span class="token operator">=</span> tf<span class="token punctuation">.</span>nn<span class="token punctuation">.</span>conv2d<span class="token punctuation">(</span>x2<span class="token punctuation">,</span>kernel<span class="token punctuation">,</span>strides<span class="token operator">=</span><span class="token punctuation">[</span><span class="token number">1</span><span class="token punctuation">,</span><span class="token number">2</span><span class="token punctuation">,</span><span class="token number">2</span><span class="token punctuation">,</span><span class="token number">1</span><span class="token punctuation">]</span><span class="token punctuation">,</span>padding<span class="token operator">=</span><span class="token string">"VALID"</span><span class="token punctuation">)</span>

sess <span class="token operator">=</span> tf<span class="token punctuation">.</span>InteractiveSession<span class="token punctuation">(</span><span class="token punctuation">)</span>
tf<span class="token punctuation">.</span>global_variables_initializer<span class="token punctuation">(</span><span class="token punctuation">)</span>
x1<span class="token punctuation">,</span>y1_1<span class="token punctuation">,</span>y1_2<span class="token punctuation">,</span>x2<span class="token punctuation">,</span>y2_1<span class="token punctuation">,</span>y2_2 <span class="token operator">=</span> sess<span class="token punctuation">.</span>run<span class="token punctuation">(</span><span class="token punctuation">[</span>x1<span class="token punctuation">,</span>y1_1<span class="token punctuation">,</span>y1_2<span class="token punctuation">,</span>x2<span class="token punctuation">,</span>y2_1<span class="token punctuation">,</span>y2_2<span class="token punctuation">]</span><span class="token punctuation">)</span>
<span class="token keyword">print</span><span class="token punctuation">(</span>x1<span class="token punctuation">.</span>shape<span class="token punctuation">)</span>         <span class="token comment">#(1, 4, 4, 3)</span>
<span class="token keyword">print</span><span class="token punctuation">(</span>y1_1<span class="token punctuation">.</span>shape<span class="token punctuation">)</span>       <span class="token comment">#(1, 2, 2, 1)</span>
<span class="token keyword">print</span><span class="token punctuation">(</span>y1_2<span class="token punctuation">.</span>shape<span class="token punctuation">)</span>       <span class="token comment">#(1, 1, 1, 1)</span>
<span class="token keyword">print</span><span class="token punctuation">(</span>x2<span class="token punctuation">.</span>shape<span class="token punctuation">)</span>         <span class="token comment">#(1, 6, 6, 3)</span>
<span class="token keyword">print</span><span class="token punctuation">(</span>y2_1<span class="token punctuation">.</span>shape<span class="token punctuation">)</span>       <span class="token comment">#(1, 3, 3, 1)</span>
<span class="token keyword">print</span><span class="token punctuation">(</span>y2_2<span class="token punctuation">.</span>shape<span class="token punctuation">)</span>       <span class="token comment">#(1, 2, 2, 1)</span>

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

下面看一个卷积的计算例子

    x1 = tf.constant([i*0.1 for i in range(16)],shape=
    	[1,4,4,1],dtype=tf.float32)
    kernel = tf.ones(shape=[3,3,1,1],dtype=tf.float32)
    conv1 = tf.nn.conv2d(x1,kernel,strides=
    	[1,1,1,1],padding="VALID")
    sess = tf.InteractiveSession()
    tf.global_variables_initializer()
    conv1 = sess.run(conv1)
    print(conv1)
1
2
3
4
5
6
7
8
9

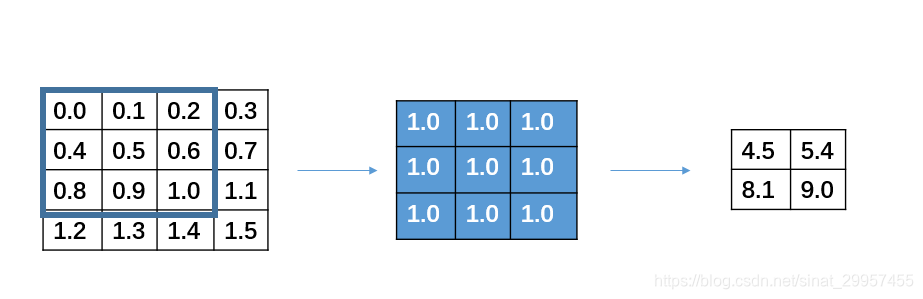
将卷积核与输入矩阵对应的位置进行乘加计算即可，对于多维输入矩阵和多维卷积核的卷积计算，将卷积后的结果进行堆叠，作为最终卷积的输出结果。

反卷积

tensorflow提供了tf.nn.conv2d_transpose函数来计算反卷积
功能说明：计算反卷积(转置卷积)

• value：4维的tensor，float类型，需要进行反卷积的矩阵
• filter：卷积核，参数格式[height，width，output_channels，in_channels]，这里需要注意output_channels和in_channels的顺序
• output_shape：一维的Tensor，设置反卷积输出矩阵的shape
• strides：反卷积的步长
• padding："SAME"和"VALID"两种模式
• data_format：和之前卷积参数一样
• name：操作的名称

if __name__ == "__main__":
    x1 = tf.constant([4.5,5.4,8.1,9.0],shape=
    	[1,2,2,1],dtype=tf.float32)
    dev_con1 = tf.ones(shape=[3,3,1,1],dtype=tf.float32)
    y1 = tf.nn.conv2d_transpose(x1,dev_con1,output_shape=
    	[1,4,4,1],strides=[1,1,1,1],padding="VALID")
    sess = tf.InteractiveSession()
    tf.global_variables_initializer()
    y1,x1 = sess.run([y1,x1])
    print(y1)
    print(x1)
1
2
3
4
5
6
7
8
9
10
11

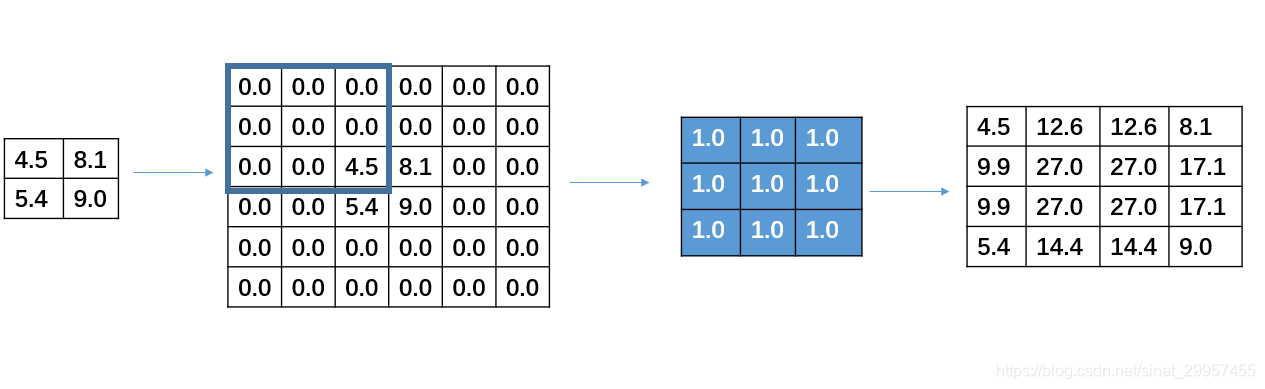
需要注意的是，通过反卷积并不能还原卷积之前的矩阵，只能从大小上进行还原，反卷积的本质还是卷积，只是在进行卷积之前，会进行一个自动的padding补0，从而使得输出的矩阵与指定输出矩阵的shape相同。框架本身，会根据你设定的反卷积值来计算输入矩阵的尺寸，如果shape不符合，则会报错。
错误提示：InvalidArgumentError (see above for traceback): Conv2DSlowBackpropInput，这时候需要检查反卷积的参数与输入矩阵之间的shape是否符合。计算规则可以根据padding为SAME还是VALID来计算输入和输出矩阵的shape是否相符合。如上例中，根据反卷积的参数来计算输入矩阵的shape：因为padding是VALID模式，所以我们套用ceil((i−k+1)/s)=ceil((4−3+1)/1)=2$ceil((i-k+1)/s)=ceil((4-3+1)/1)=2$ceil((i−k+1)/s)=ceil((4−3+1)/1)=2，而输入矩阵x1的shape刚好是2*2，所以符合。
上面介绍的反卷积的stride是1，接下来看一个stride不为1的例子

    x1 = tf.constant([4.5,5.4,8.1,9.0],shape=
    	[1,2,2,1],dtype=tf.float32)
    dev_con1 = tf.ones(shape=[3,3,1,1],dtype=tf.float32)
    y1 = tf.nn.conv2d_transpose(x1,dev_con1,output_shape=
    	[1,6,6,1],strides=[1,2,2,1],padding="VALID")
    sess = tf.InteractiveSession()
    tf.global_variables_initializer()
    y1,x1 = sess.run([y1,x1])
<span class="token keyword">print</span><span class="token punctuation">(</span>x1<span class="token punctuation">)</span>
<span class="token keyword">print</span><span class="token punctuation">(</span>y1<span class="token punctuation">)</span>

1
2
3
4
5
6
7
8
9
10
11

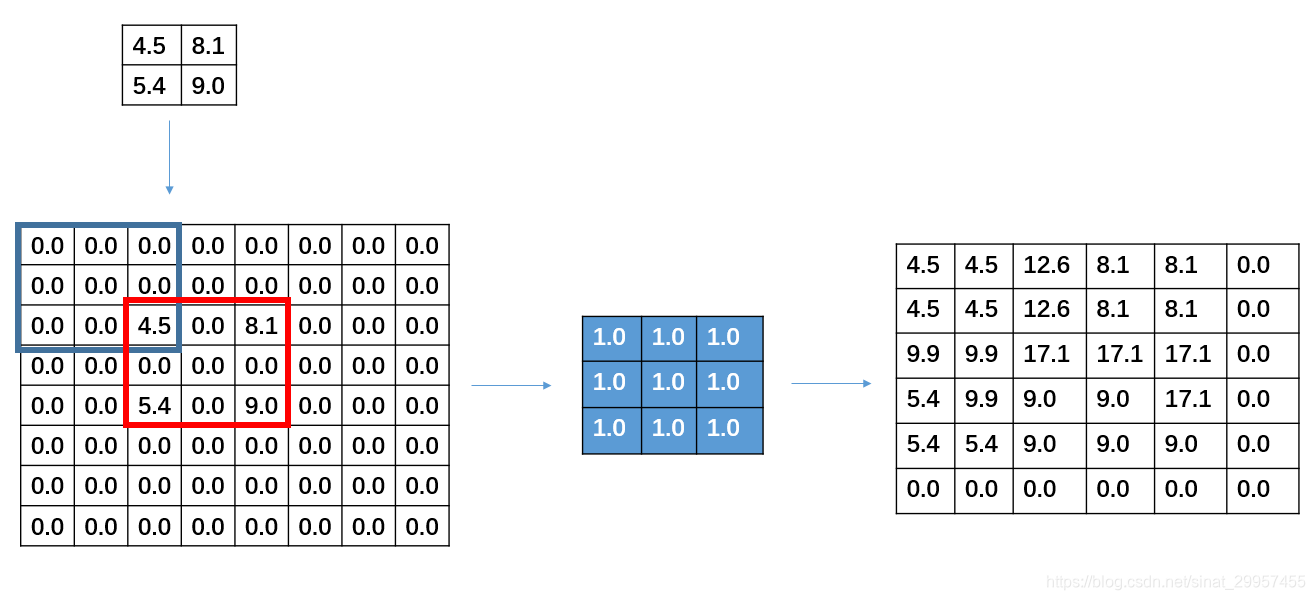
需要注意的是，在进行反卷积的时候设置的stride并不是指反卷积在进行卷积时候卷积核的移动步长，而是被卷积矩阵填充的padding，仔细观察红色框内可以发现之前输入矩阵之间有一行和一列0的填充。

                                </div>
            <link href="https://csdnimg.cn/release/phoenix/mdeditor/markdown_views-e44c3c0e64.css" rel="stylesheet">
                </div>