显然只需要算出每个数比前面所有数大的期望然后全部加起来就好了,一个数的期望怎么算呢?
对于一个数我们需要考虑比它大的数,因为比它小的数放它前面放它后面都可以,但是比它大的数只能放它后面。考虑大于等于它的数有n-i+1个,排列有(n-i+1)!种,但是它必须放在所有数的前面,也就是合法的排列只有(n-i)!种,那么期望(n-i)!/(n-i+1)!=1/(n-i+1)。
于是总的期望为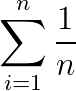
这是个调和级数,貌似可以用某个公式计算,但是这个时候可以祭出神器,分段打表!然后就AC了233

#include<iostream> #include<cstring> #include<cstdlib> #include<cstdio> #include<cmath> #include<algorithm> using namespace std; const int maxn=500010,inf=1e9; int n; double num[1000]={0,16.69531137,17.38845852,17.79392362,18.08160569,18.30474924,18.48707079,18.64122147,18.77475286,18.89253590,18.99789641,19.09320659,19.18021797,19.26026068,19.33436865,19.40336152,19.46790004,19.52852466,19.58568308,19.63975030,19.69104359,19.73983376,19.78635377,19.83080553,19.87336515,19.91418714,19.95340786,19.99114818,20.02751583,20.06260715,20.09650870,20.12929852,20.16104722,20.19181888,20.22167184,20.25065938,20.27883026,20.30622923,20.33289748,20.35887296,20.38419077,20.40888338,20.43298094,20.45651143,20.47950095,20.50197381,20.52395271,20.54545892,20.56651233,20.58713161,20.60733432,20.62713695,20.64655504,20.66560323,20.68429536,20.70264450,20.72066301,20.73836258,20.75575433,20.77284876,20.78965588,20.80618518,20.82244570,20.83844604,20.85419440,20.86969859,20.88496606,20.90000394,20.91481902,20.92941782,20.94380656,20.95799119,20.97197744,20.98577076,20.99937641,21.01279943,21.02604466,21.03911674,21.05202014,21.06475917,21.07733795,21.08976047,21.10203056,21.11415192,21.12612812,21.13796257,21.14965861,21.16121944,21.17264813,21.18394769,21.19512099,21.20617082,21.21709989,21.22791081,21.23860610,21.24918821,21.25965951,21.27002229,21.28027880,21.29043117,21.30048150,21.31043183,21.32028413,21.33004030,21.33970222,21.34927167,21.35875041,21.36814015,21.37744254,21.38665920,21.39579168,21.40484152,21.41381019,21.42269914,21.43150976,21.44024344,21.44890151,21.45748525,21.46599594,21.47443481,21.48280306,21.49110186,21.49933236,21.50749567,21.51559288,21.52362505,21.53159322,21.53949840,21.54734158,21.55512372,21.56284577,21.57050864,21.57811324,21.58566044,21.59315112,21.60058609,21.60796620,21.61529224,21.62256500,21.62978525,21.63695374,21.64407121,21.65113837,21.65815595,21.66512462,21.67204506,21.67891794,21.68574390,21.69252359,21.69925762,21.70594661,21.71259115,21.71919184,21.72574924,21.73226392,21.73873643,21.74516732,21.75155712,21.75790635,21.76421552,21.77048513,21.77671568,21.78290765,21.78906152,21.79517774,21.80125679,21.80729910,21.81330513,21.81927530,21.82521003,21.83110975,21.83697487,21.84280579,21.84860291,21.85436662,21.86009729,21.86579531,21.87146105,21.87709487,21.88269712,21.88826817,21.89380835,21.89931800,21.90479747,21.91024707,21.91566714,21.92105799,21.92641993,21.93175328,21.93705833,21.94233539,21.94758474,21.95280669,21.95800151,21.96316948,21.96831087,21.97342598,21.97851504,21.98357835,21.98861614,21.99362868,21.99861622,22.00357901,22.00851730,22.01343131,22.01832130,22.02318748,22.02803011,22.03284940,22.03764557,22.04241885,22.04716945,22.05189759,22.05660348,22.06128733}; inline void read(int &k) { int f=1;k=0;char c=getchar(); while(c<'0'||c>'9')c=='-'&&(f=-1),c=getchar(); while(c<='9'&&c>='0')k=k*10+c-'0',c=getchar(); k*=f; } int main() { read(n); double ans=num[n/10000000]; for(;n%10000000;n--)ans+=1.0/n; printf("%.8lf",ans); }
