bzoj2216: [Poi2011]Lightning Conductor（分治决策单调性优化）

　　每个pi要求

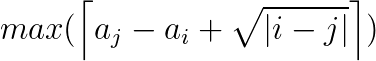
　　这个只需要正反DP（？）一次就行了，可以发现这个是有决策单调性的，用分治优化

#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
const int maxn=500010,inf=1e9;
int n;
int a[maxn],f[maxn][2];
void read(int &k)
{
    int f=1;k=0;char c=getchar();
    while(c<'0'||c>'9')c=='-'&&(f=-1),c=getchar();
    while(c<='9'&&c>='0')k=k*10+c-'0',c=getchar();
    k*=f;                                                                                                                                                                       
}
void solve(int l,int r,int L,int R,int ty)
{
    if(l>r||L>R)return;
    int mid=(l+r)>>1,pos;
    double mx=0.0;
    for(int i=L;i<=R&&i<=mid;i++)
    {
        if((double)a[i]-a[mid]+sqrt(mid-i)>=mx)
        mx=(double)a[i]-a[mid]+sqrt(mid-i),pos=i;
    }
    f[mid][ty]=(int)ceil(mx);
    solve(l,mid-1,L,pos,ty);solve(mid+1,r,pos,R,ty);
}
int main()
{
    read(n);
    for(int i=1;i<=n;i++)read(a[i]);
    solve(1,n,1,n,0);
    reverse(a+1,a+1+n);
    solve(1,n,1,n,1);
    for(int i=1;i<=n;i++)printf("%d
",max(f[i][0],f[n-i+1][1]));
}