bzoj1211: [HNOI2004]树的计数（purfer编码）

　　BZOJ1005的弱化版，不想写高精度就可以写这题嘿嘿嘿

　　purfer编码如何生成？每次将字典序最小的叶子节点删去并将其相连的点加入序列中，直到树上剩下两个节点，所以一棵有n个节点的树purfer编码长度为n-2。

　　purfer编码如何还原一棵树？从前往后扫purfer编码，每次找到不在编码中的没有被选择过的字典序最小的点，并将purfer编码第一个点与这个点连边并删去。

　　purfer编码的性质？

　　①度数为d[i]的点在purfer编码中出现d[i]-1次。

　　②每一个purfer编码对应一棵唯一的树。

　　知道了这些之后，我们就能大概有一个思路了，求多少棵树相当于求多少个purfer编码满足条件。

　　第i个点度数为d[i]，那么在purfer编码中出现d[i]-1次，编码的长度为n-2，于是总的方案数为：

　　

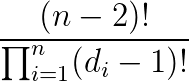
　　虽然答案不会爆long long但是计算过程会爆，于是必须分解质因数来写。

#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio> 
#include<algorithm>
#define ll long long 
using namespace std;
const int maxn=160,inf=1e9;
int n,sum;
int cnt[maxn],d[maxn];
ll ans=1;
void read(int &k)
{
    int f=1;k=0;char c=getchar();
    while(c<'0'||c>'9')c=='-'&&(f=-1),c=getchar();
    while(c<='9'&&c>='0')k=k*10+c-'0',c=getchar();
    k*=f;
}
void dec(int x,int y)
{
    for(int i=2;i*i<=x;i++)
    while(x%i==0)cnt[i]+=y,x/=i;
    if(x^1)cnt[x]+=y;
}
ll power(ll a,int b)
{
    ll ans=1;
    while(b)
    {
        if(b&1)ans*=a;
        a*=a;
        b>>=1;
    }
    return ans;
}
int main()
{
    read(n);
    for(int i=1;i<=n;i++)
    {
        read(d[i]);sum+=d[i]-1;
        if(!d[i]&&n!=1)return puts("0"),0;
    }
    if(sum!=n-2)return puts("0"),0;
    for(int j=2;j<=n-2;j++)dec(j,1);
    for(int i=1;i<=n;i++)
    for(int j=2;j<d[i];j++)
    dec(j,-1);
    for(int i=2;i<=n-2;i++)
    if(cnt[i])ans*=power(i,cnt[i]);
    printf("%lld
",ans);
    return 0;
}