安全散列算法SHA(Secure Hash Algorithm)是美国国家安全局 (NSA) 设计,美国国家标准与技术研究院(NIST) 发布的一系列密码散列函数,包括 SHA-1、SHA-224、SHA-256、SHA-384 和 SHA-512 等变体。主要适用于数字签名标准(DigitalSignature Standard DSS)里面定义的数字签名算法(Digital Signature Algorithm DSA)。下面以 SHA-1为例,介绍该算法计算消息摘要的原理。
SHA1有如下特性:不可以从消息摘要中复原信息;两个不同的消息不会产生同样的消息摘要。
一、术语和概念
(一)位(Bit),字节(Byte)和字(Word)
SHA1始终把消息当成一个位(bit)字符串来处理。本文中,一个“字”(Word)是32位,而一个“字节”(Byte)是8位。比如,字符串“abc”可以被转换成一个位字符串:01100001 01100010 01100011。它也可以被表示成16进制字符串:0x616263.
(二)运算符和符号
下面的逻辑运算符都被运用于“字”(Word)
X^Y = X,Y逻辑与
X / Y = X,Y逻辑或
X XOR Y= X,Y逻辑异或
~X = X逻辑取反
X+Y定义如下:
字 X 和Y 代表两个整数 x 和y, 其中0 <= x < 2^32 且 0 <= y < 2^32. 令整数z= (x + y) mod 2^32. 这时候 0 <= z < 2^32. 将z转换成字Z,那么就是 Z = X + Y.
循环左移位操作符Sn(X)。X是一个字,n是一个整数,0<=n<=32。Sn(X)= (X<<n)or(x>>32-n)
X<<n< span="">定义如下:抛弃最左边的n位数字,将各个位依次向左移动n位,然后用0填补右边的n位(最后结果还是32位)。X>>n是抛弃右边的n位,将各个位依次向右移动n位,然后在左边的n位填0。因此可以叫Sn(X)位循环移位运算
二、SHA1算法描述
在SHA1算法中,我们必须把原始消息(字符串,文件等)转换成位字符串。SHA1算法只接受位作为输入。假设我们对字符串“abc”产生消息摘要。首先,我们将它转换成位字符串如下:
01100001 0110001001100011
―――――――――――――
‘a’=97 ‘b’=98‘c’=99
这个位字符串的长度为24。下面我们需要5个步骤来计算MD5。
(一)补位
消息必须进行补位,以使其长度在对512取模以后的余数是448。也就是说,(补位后的消息长度)%512 = 448。即使长度已经满足对512取模后余数是448,补位也必须要进行。
补位是这样进行的:先补一个1,然后再补0,直到长度满足对512取模后余数是448。总而言之,补位是至少补一位,最多补512位。还是以前面的“abc”为例显示补位的过程。
原始信息:01100001 01100010 01100011
补位第一步:0110000101100010 01100011 1
首先补一个“1”
补位第二步:0110000101100010 01100011 10…..0
然后补423个“0”
我们可以把最后补位完成后的数据用16进制写成下面的样子
61626380 0000000000000000 00000000
00000000 0000000000000000 00000000
00000000 0000000000000000 00000000
00000000 00000000
现在,数据的长度是448了,我们可以进行下一步操作。
(二)补长度
所谓的补长度是将原始数据的长度补到已经进行了补位操作的消息后面。通常用一个64位的数据来表示原始消息的长度。如果消息长度不大于2^64,那么第一个字就是0。在进行了补长度的操作以后,整个消息就变成下面这样了(16进制格式)
61626380 0000000000000000 00000000
00000000 0000000000000000 00000000
00000000 0000000000000000 00000000
00000000 0000000000000000 00000018
如果原始的消息长度超过了512,我们需要将它补成512的倍数。然后我们把整个消息分成一个一个512位的数据块,分别处理每一个数据块,从而得到消息摘要。
(三)使用的常量
一系列的常量字K(0),K(1), ... , K(79),如果以16进制给出。它们如下:
Kt = 0x5A827999 (0<= t <= 19)
Kt = 0x6ED9EBA1 (20<= t <= 39)
Kt = 0x8F1BBCDC (40<= t <= 59)
Kt = 0xCA62C1D6 (60<= t <= 79).
(四)需要使用的函数
在SHA1中我们需要一系列的函数。每个函数ft (0 <= t <= 79)都操作32位字B,C,D并且产生32位字作为输出。ft(B,C,D)可以如下定义
ft(B,C,D) = (B ANDC) or ((NOT B) AND D) ( 0 <= t <= 19)
ft(B,C,D) = B XOR CXOR D (20 <= t <= 39)
ft(B,C,D) = (B ANDC) or (B AND D) or (C AND D) (40 <= t <= 59)
ft(B,C,D) = B XOR CXOR D (60 <= t <= 79).
(五)计算消息摘要
必须使用进行了补位和补长度后的消息来计算消息摘要。计算需要两个缓冲区,每个都由5个32位的字组成,还需要一个80个32位字的缓冲区。第一个5个字的缓冲区被标识为A,B,C,D,E。第二个5个字的缓冲区被标识为H0,H1, H2, H3, H4。80个字的缓冲区被标识为W0,W1,..., W79
另外还需要一个一个字的TEMP缓冲区。
为了产生消息摘要,在第4部分中定义的16个字的数据块M1,M2,..., Mn
会依次进行处理,处理每个数据块Mi 包含80个步骤。
在处理每个数据块之前,缓冲区{Hi} 被初始化为下面的值(16进制)
H0 = 0x67452301
H1 = 0xEFCDAB89
H2 = 0x98BADCFE
H3 = 0x10325476
H4 = 0xC3D2E1F0.
现在开始处理M1, M2,... , Mn。为了处理 Mi,需要进行下面的步骤
(1). 将Mi 分成 16 个字 W0, W1, ... , W15,W0 是最左边的字
(2). 对于t = 16 到 79 令 Wt = S1(Wt-3 XOR Wt-8XOR Wt- 14 XOR Wt-16).
(3). 令A = H0, B = H1, C = H2, D = H3, E = H4.
(4) 对于t = 0 到 79,执行下面的循环
TEMP = S5(A) +ft(B,C,D) + E + Wt + Kt;
E = D; D = C; C =S30(B); B = A; A = TEMP;
(5). 令H0 = H0 + A, H1 = H1 + B, H2 = H2 + C, H3 = H3 + D, H4 = H4 + E.
在处理完所有的 Mn, 后,消息摘要是一个160位的字符串,以下面的顺序标识
H0 H1 H2 H3 H4.
对于SHA256、SHA384、SHA512。你也可以用相似的办法来计算消息摘要。对消息进行补位的算法完全是一样的。
三、SHA算法被破解了吗?
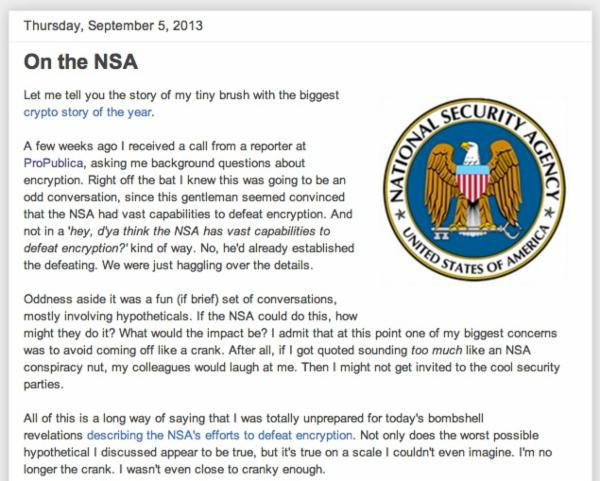
2013年9月10日美国约翰霍普金斯大学的计算机科学教授,知名的加密算法专家,Matthew Green被NSA要求删除他的一份关于破解加密算法的与NSA有关的博客。 同时约翰霍普金斯大学服务器上的该博客镜像也被要求删除。

加密算法专家,美国约翰霍普金斯大学教授Matthew Green
但当记者向该大学求证时,该校称从未收到来自NSA的要求要删除博客或镜像的资料,但记者却无法在原网址再找到该博客。幸运的是,从谷歌的缓存可以找到该博客。该博客提到NSA每年花费2.5亿美元来为自己在解密信息方面获取优势,并列举了NSA的一系列见不得人的做法。
在BitcoinTalk上,已经掀起了一轮争论:到底SHA-2是否安全?
部分认为不安全的观点包括:
- NSA制造了sha-2, 我们不相信NSA,他们不可能不留后门。
- 棱镜事件已经明白的告诉我们,政府会用一切可能的手段来监视与解密。
- 虽然有很多人会研究SHA-2,且目前没有公开的证据表明有漏洞。但没有公开这并不能代表就没有,因为发现漏洞的人一定更倾向于保留这个秘密来自己利用,而不是公布。
部分认为安全的观点包括:
- SHA-2是应用广泛的算法,应该已经经历了实践的检验。
- 美国的对头中国和俄国都有很多杰出的数学家,如果有问题的话,他们肯定已经发现了。
- 如果真的不安全,世界上安全的东西就太少了,我不能生活在提心吊胆里,所以我选择相信安全。