线段树相关(研究总结,线段树)
线段树是信息学竞赛中的一种常用数据结构,能够很方便的进行区间查找和修改操作。
引入
假设我们现在有一列数,我们需要支持一下操作:
1.修改某个数的值
2.询问一段区间的和
我们很容易想到朴素的做法,用一个数组存下所有的值,如果是修改操作就直接修改,如果是询问就循环统计一遍。但这样效率不高。
或许有人可以想出另外一个算法,就是用前缀和来优化,Sum[i]表示1到i的和,这样方便了询问操作,但对于修改操作,就要修改很多Sum的值,效率同样不高。
怎么办呢?我们可以用线段树解决
线段树
对于下面这个区间

我们可以把其分成两个

再对分出的两个区间进行分离操作
像这样重复操作,我们就可以得到一棵线段树
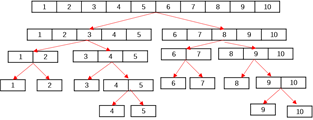
一些小性质与本文习惯约定
通过观察我们可以发现,如果按从上到下,从左到右的顺序,把每一个区间看作一个点并给其编号,我们可以得出如下规律:
对于每一个节点i,我们假设其代表的区间是[x,y],定义mid=(x+y)/2,那么,它的左区间[x,mid]的编号就是i*2,而它的右区间[mid+1,y]编号就是i*2+1
为了方便叙述,下面我们称i*2为i的左子节点,i*2+1为i的右子节点
另外,本文中约定线段树的节点编号从1开始
线段树的简单操作
现在有了线段树,但它有什么用呢?
先简单的说一下,假设我们现在要查找[x,y]的和,并且我们现在正好在线段树的这个[x,y]区间,那么我们就可以直接返回这个点上的Sum域(当然要提前确定好,这是可以在建树的时候顺带完成的)
比如说,对于下面这个数组:

我们想建立一棵线段树来处理其任意两点之间的和,那么我们可以这样:
对于每一个线段树的节点,我们维护一个Sum表示当前线段树的节点中覆盖的区间的和,表示出来就是这样:
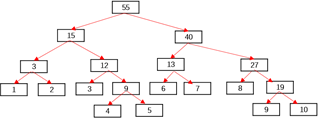
而由于我们知道线段树的性质是左儿子是i*2而右儿子是i*2+1,所以我们甚至不需要存下对应的左儿子右儿子编号。
首先我们来讲一下查询操作
在本例中,查询是查询一个区间内的值之和,假设当前我们要查询的区间是[l0,r0],当前我们所在的线段树的节点是now(开始时就是1啦),当前我们所在的线段树节点的左右区间是[l,r],再定义mid=(l+r)/2,也就是中间结点。
我们定义查询的函数是Query(l0,r0,l,r,now)我们会碰到如下的三种情况:
1.查询区间完全在左区间内(我们用透明的框表示当前所在的线段树区间,用蓝色的框表示我们的查询区间,红色的框代表mid所在)

对于这种情况,我们直接递归地调用查找左子树区间就可以了,即Query(l0,r0,l,mid,now*2)
2.类似的,查询区间完全在右区间内时

递归调用Query(l0,r0,mid+1,now*2+1)
3.稍微复杂一点的就是这第三种情况,查询区间横跨左右

这个时候我们要分别对左区间和右区间进行递归查询并累加Query(l0,mid,l,mid,now*2)+Query(mid+1,r0,mid+1,r,now*+1)
其实还有第四种情况,就是l0l,r0r,此时直接返回该区间的Sum值就可以了
总结一下,代码如下:
int Query(int l0,int r0,int l,int r,int now)
{
if ((l0==l)&&(r0==r))
return T[now].data;//T就是线段树,data就是值域
int mid=(l+r)/2;
if (l0>=mid+1)
{
return Query(l0,r0,mid+1,r,now*2+1);
}
else
if (r0<=mid)
{
return Query(l0,r0,l,mid,now*2);
}
else
{
return Query(l0,mid,l,mid,now*2)+Query(mid+1,r0,mid+1,r,now*2+1);
}
}
然后我们来讲一下修改操作
相对于查询操作,修改操作相对好理解。
同样也是进行递归的操作,若修改的数在左区间,则递归到左子树,否则递归到右子树。
但要注意的是,修改的时候要记得一路修改所有经过的线段树节点的值。
void Updata(int num,int data,int l,int r,int now)//num是我们要修改的数的编号,data是我们要把num修改成什么,l和r分别是当前所在线段树的now节点的左右区间端点
{
if (l==r)
{
T[now].data=data;
return;
}
int mid=(l+r)/2;
if (num<=mid)
Updata(num,data,l,mid,now*2);//分别进入左右子树
else
Updata(num,data,mid+1,r,now*2+1);
T[now].data+=data;//注意一路修改
}
在有些题目中,递归调用可能会爆栈,而又因为修改操作的特殊性(它不会涉及到同时操作两个区间),我们可以把递归的方式改成不递归的,,其原理与递归方式一样
void Updata(int num,int data)
{
int now=1;
int l=1,r=n;
do
{
int mid=(l+r)/2;
T[now].data+=data;
if (l==r)
break;
if (num<=mid)
{
r=mid;
now=now*2;
}
else
{
l=mid+1;
now=now*2+1;
}
}
while (1);
return;
}
线段树的其他操作
在了解了线段树的基本操作后,相信读者已经对线段树有了基本的了解。
线段树其实还有很多操作,它们都是建立在对线段树的理解上面的,笔者这里仅列出常用的一种,其它的读者可以在遇到相关题目时自行推导。
在上文中,我们讲到了线段树的修改操作,但准确地说,这是线段树的单源修改操作,如果我们要对数列的一段区间的数进行修改呢?(比如说,我们要使得[x,y]中的每一个数都加上一个输入的数)
一种解决方法就是调用(y-x+1)次单源修改操作,但这样时间复杂度太高。
我们回想一下线段树的原理:它是区间的操作。那我们能否把区间修改与区间操作相结合起来呢?
当然可以。我们在每一个线段树的值域中再引入一个Lazy,或者叫做迟缓标记,在我们上面的例子中(即使得[x,y]中的每一个数都加上一个数),它表示的就是在当前线段树节点所覆盖的每一个点上都加上Lazy。
举个例子,现在我们要在一个[1,10]的数列中,给l0=1,r0=5内的所有数都加上1,那么我们在递归修改的时候,首先进入的是l=1,r=10的区间,然后进入l=1,r=5的区间,这是我们发现l0l且r0r,所以我们直接给该节点上的Laze+=1。
那么对应的,因为我们加入了迟缓标记,我们就要修改一下查询和修改操作。在每一次进入下一层时,首先要下放当前点中的Lazy标记,因为加入迟缓标记后,该层下面的点都是没有修改的,此时我们要向下查询的话就要临时把Lazy标记中的内容向下传递,这就相当于迟缓了修改操作(现在知道为什么叫迟缓标记了吧)
查询操作:
int Query(int l0,int r0,int l,int r,int now);
{
if ((l0==l)&&(r0==r))//如果符合就直接返回
{
return T[now].data+T[now].Lazy*(l-r+1);
}
int Lazy=T[now].lazy;//下放Lazy标记
T[now].data+=Lazy*(l-r+1);
T[now*2].lazy+=Lazy;
T[now*2+1].lazy+=Lazy;
T[now].lazy=0;
int mid=(l+r)/2;
if (r0<=mid)//向下递归
return Query(l0,r0,l,mid,now*2);
else
if (l0>=mid+1)
return Query(l0,r0,mid+1,r,now*2+1);
else
return Query(l0,mid,l,mid,now*2)+Query(mid+1,r0,mid+1,r,now*2+1);
}
修改操作:
void Updata(int l0,int r0,int l,int r,int now,int data)
{
if ((l0==l)&&(r0==r))
{
T[now].lazy=data;
return;
}
int Lazy=T[now].lazy;//向下传递Lazy
T[now].data+=Lazy*(l-r+1);
T[now*2].lazy+=Lazy;
T[now*2+1].lazy+=Lazy;
T[now].lazy=0;
int mid=(l+r)/2;
if (r0<=mid)
Updata(l0,r0,l,mid,now*2,data);
else
if (l0>=mid+1)
Updata(l0,r0,mid+1,r,now*2+1,data);
else
{
Updata(l0,mid,l,mid,now*2,data);
Updata(mid+1,r0,mid+1,r,now*2+1,data);
}
return;
}
好题推荐
请到我的博客右侧线段树分类中查看
欢迎大佬查错,谢谢