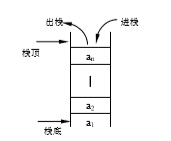
栈
栈的定义
栈是限制在表的一端进行插入和删除的线性表。允许插入、删除的这一端称为栈顶,另 一个固定端称为栈底。当表中没有元素时称为空栈。
栈顶:通常将表中允许进行插入、删除操作的一端称为栈顶 (Top),因此栈顶的当前位 置是动态变化的,它由一个称为栈顶指针的位置指示器指示。
栈底:同时表的另一端被称为栈底 (Bottom)。当栈中没有元素时称为空栈。栈的插入 操作被形象地称为进栈或入栈,删除操作称为出栈或退栈。
栈是运算受限的线性表,线性表的存储结构对栈也是适用的,只是操作不同而已。
利用顺序存储方式实现的栈称为顺序栈。
(1) InitStack(S)
操作前提:S 为未初始化的栈。 操作结果:将 S 初始化为空栈。
(2) ClearStack(S)
操作前提:栈 S 已经存在。 操作结果:将栈 S 置成空栈。
(3) IsEmpty(S)
操作前提:栈 S 已经存在。 操作结果:判栈空函数,若 S 为空栈则函数值为“TRUE”,否则为“FALSE”。
(4) IsFull(S)
操作前提:栈 S 已 经存在。 操作结果:判栈满函数,若 S 栈已满,则函数值为“TRUE”,否则为“FALSE”。
(5) Push(S,x)
操作前提:栈 S 已经存在。 操作结果:在 S 的顶部插入(亦称压入)元素 x;若 S 栈未满,将 x 插入栈顶 位置,若栈已满,则返回 FALSE,表示操作失败,否则返回 TRUE。
(6) Pop(S, x)
操作前提:栈 S 已经存在。 操作结果:删除(亦称弹出)栈 S 的顶部元素,并用 x 带回该值; 若栈为空,返回值为 FALSE,表示操作失败,否则返回 TRUE。
(7) GetTop(S, x)
操作前提:栈 S 已经存在。 操作结果:取栈 S 的顶部元素赋给 x 所指向的单元。与 Pop(S, x)不同之处在 于 GetTop(S,x)不改变栈顶的位置。
与线性表类似,栈的动态分配顺序存储结构如 下:
#define STACK_INIT_SIZE 100 //存储空间的初始分配量
#define STACKINCREMENT 10 //存储空间的分配增量
typedef struct{
SElemType *base; //在栈构造之前和销毁之后,base 的值为 NULL
SElemType *top; //栈顶指针
int stacksize; //当前已分配的存储空间
}SqStack;
需要注意,在栈的动态分配顺序存储结构中,base 始终指向栈底元素,非空栈中的 top 始终在栈顶元素的下一个位置。
下面是顺序栈上常用的基本操作的实现。
(1)入栈:若栈不满,则将 e 插入栈顶。
int Push (SqStack &S, SElemType e) {
if (S.top-S.base>=S.stacksize)
{……} //栈满,追加存储空间
*S.top++ = e; //top始终在栈顶元素的下一个位置 return OK;
}
(2)出栈:若栈不空,则删除 S 的栈顶元素,用 e 返回其值,并返回 OK,否则返回 ERROR。
int Pop (SqStack &S, SElemType &e) {
if (S.top==S.base) return ERROR;
e = *--S.top;
return OK;
}
出栈和读栈顶元素操作,先判栈是否为空,为空时不能操作,否则产生错误。通常栈空常作为一种控制转移的条件。
顺序栈的两栈共享
栈的应用非常广泛,经常会出现在一个程序中需要同时使用多个栈的情况。若使用顺序 栈,会因为对栈空间大小难以准确估计,从而产生有的栈溢出、有的栈空间还很空闲的情况。
多栈共享技术:
可以让多个栈共享一个足够大的数组空间,通过利用栈的动态特性来使 其存储空间互相补充,这就是多栈共享技术。
在顺序栈的共享技术中最常用的是两个栈的共享技术即双端栈:它主要利用了栈“栈底 位置不变,而栈顶位置动态变化”的特性。首先为两个栈申请一个共享的一维数组空间 S[M], 将两个栈的栈底分别放在一维数组的两端,分别是 0,M-1。由于两个栈顶动态变化,这样 可以形成互补,使得每个栈可用的最大空间与实际使用的需求有关。由此可见,两栈共享要 比两个栈分别申请 M/2 的空间利用率要高。两栈共享的数据结构定义如下:
#define M 100
typedef struct
{
StackElementType Stack[M];
StackElementType top[2]; /*top[0]和 top[1]分别为两个栈顶指示器*/ }DqStack;
两个栈共用时的初始化、进栈和出栈操作 的算法:
⑴ 初始化操作。
【算法描述】
void InitStack(DqStack *S)
{
S->top[0]=-1;
S->top[1]=M;
}
⑵ 进栈操作。
【算法描述】
int Push(DqStack *S, StackElementType x, int i)
{/*把数据元素 x 压入 i 号堆栈*/
if(S->top[0]+1==S->top[1]) /*栈已满*/
return(FALSE);
switch(i)
{
case 0:
S->top[0]++;
S->Stack[S->top[0]]=x;
break;
case 1:
S->top[1]--;
S->Stack[S->top[1]]=x;
break;
default: /*参数错误*/
return(FALSE)
}
return(TRUE);
}
⑶ 出栈操作。
【算法描述】
int Pop(DqStack *S, StackElementType *x, int i)
{/* 从 i 号堆栈中弹出栈顶元素并送到 x 中 */
switch(i)
{
case 0:
if(S->top[0]==-1) return(FALSE);
*x=S->Stack[S->top[0]];
S->top[0]--;
break;
case 1:
if(S->top[1]==M) return(FALSE);
*x=S->Stack[S->top[1]];
S->top[1]++;
break;
default:
return(FALSE);
}
return(TRUE);
}
栈的链式实现
链栈即采用链表作为存储结构实现的栈。
为便于操作,这里采用带头结点的单链表实现栈。由于栈的插入和删除操作仅限制在表头位置进行,所以链表的表头指针就作为栈顶指 针,如下图所示。
栈链示意图:
在上图中,top 为栈顶指针,始终指向当前栈顶元素前面的头结点。若 top->next=NULL, 则代表栈空。采用链栈不必预先估计栈的最大容量,只要系统有可用空间,链栈就不会出现溢出。采用链栈时,栈的各种基本操作的实现与单链表的操作类似,对于链栈,在使用完毕 时,应该释放其空间。
链栈的结构可用 C 语言定义如下:
typedef struct node
{
StackElementType data;
struct node *next;
}LinkStackNode;
typedef LinkStackNode *LinkStack;
进栈、出栈等最主要的运算 实现。
⑴ 进栈操作
【算法描述】
int Push(LinkStack top, StackElementType x)
/* 将数据元素 x 压入栈 top 中 */
{
LinkStackNode * temp;
temp=(LinkStackNode * )malloc(sizeof(LinkStackNode));
if(temp==NULL) return(FALSE); /* 申请空间失败 */
temp->data=x;
temp->next=top->next;
top->next=temp; /* 修改当前栈顶指针 */
return(TRUE);
}
⑵ 出栈操作
【算法描述】
int Pop(LinkStack top, StackElementType *x)
{ /* 将栈 top 的栈顶元素弹出,放到 x 所指的存储空间中 */
LinkStackNode * temp;
temp=top->next;
if(temp==NULL) /*栈为空*/
return(FALSE);
top->next=temp->next;
*x=temp->data;
free(temp); /* 释放存储空间 */
return(TRUE);
}
int Pop(LinkStack top, StackElementType *x)
{ /* 将栈 top 的栈顶元素弹出,放到 x 所指的存储空间中 */
LinkStackNode * temp;
temp=top->next;
if(temp==NULL) /*栈为空*/
return(FALSE);
top->next=temp->next;
*x=temp->data;
free(temp); /* 释放存储空间 */
return(TRUE);
}
int Pop(LinkStack top, StackElementType *x)
{ /* 将栈 top 的栈顶元素弹出,放到 x 所指的存储空间中 */
LinkStackNode * temp;
temp=top->next;
if(temp==NULL) /*栈为空*/
return(FALSE);
top->next=temp->next;
*x=temp->data;
free(temp); /* 释放存储空间 */
return(TRUE);
}
栈的应用举例
由于栈的“先进先出”特点,在很多实际问题中都利用栈做一个辅助的数据结构来进行求解。
1、数值转换
2、表达式求值
表达式求值是程序设计语言编译中一个基本的问题,它的实现也是需要栈的加入。下 面的算法是由运算符优先法对表达式求值。在此仅限于讨论只含二目运算符的算术表达式。
(1)中缀表达式求值
中缀表达式:每个二目运算符在两个运算量的中间,假设所讨论的算术运算符包括:+ 、 - 、、/、%、^(乘方)和括号()。
设运算规则为:
.运算符的优先级为:()——> ^ ——>*、/、%——> +、- ;
.有括号出现时先算括号内的,后算括号外的,多层括号,由内向外进行;
.乘方连续出现时先算右面的。
表达式作为一个满足表达式语法规则的串存储,如表达式“3*2^(4+2*2-1*3)-5”,它的求值过程为:自左向右扫描表达式,当扫描到 3*2 时不能马上计算,因为后面可能还有更高的运算,正确的处理过程是:需要两个栈:对象栈 s1 和运算符栈 s2。当自左至右扫描表达式的每一个字符时,若当前字符是运算对象,入对象栈,是运算符时,若这个运算符比栈顶运算符高则入栈,继续向后处理,若这个运算符比栈顶运算符低则从对象栈出栈两个运算量, 从运算符栈出栈一个运算符进行运算,并将其运算结果入对象栈,继续处理当前字符,直到遇到结束符。
为了处理方便,编译程序常把中缀表达式首先转换成等价的后缀表达式,后缀表达式的运算符在运算对象之后。在后缀表达式中,不在引入括号,所有的计算按运算符出现的顺序, 严格从左向右进行,而不用再考虑运算规则和级别。中缀表达式“3*2^(4+2*2-1*3)-5 ”的后 缀表达式为:“32422*+13-^*5-”
(2) 后缀表达式求值
计算一个后缀表达式,算法上比计算一个中缀表达式简单的多。这是因为表达式中即无括号又无优先级的约束。具体做法:只使用一个对象栈,当从左向右扫描表达式时,每遇到一个操作数就送入栈中保存,每遇到一个运算符就从栈中取出两个操作数进行当前的计算, 然后把结果再入栈,直到整个表达式结束,这时送入栈顶的值就是结果。
下面是后缀表达式求值的算法,在下面的算法中假设,每个表达式是合乎语法的,并且 假设后缀表达式已被存入一个足够大的字符数组 A 中,且以‘#’为结束字符,为了简化问题, 限定运算数的位数仅为一位且忽略了数字字符串与相对应的数据之间的转换的问题。
typedef char SElemType ;
double calcul_exp(char *A){ //本函数返回由后缀表达式 A 表示的表达式运算结果 SqStack s ;
ch=*A++ ; InitStack(s) ;
while ( ch != ’#’ ){
if (ch!=运算符) Push (s , ch) ;
else {
Pop (s , &a) ; Pop (s , &b) ; //取出两个运算量 switch (ch).{
case ch= =’+’: c=a+b ; break ;
case ch= =’-’: c=a-b ; break ;
case ch= =’*’: c=a*b ; break ;
case ch= =’/’: c=a/b ; break ;
case ch= =’%’: c=a%b ; break ;
}
Push (s, c) ;
}
ch=*A++ ;
}
Pop ( s , result ) ;
return result ;
}
(3) 中缀表达式转换成后缀表达式:
将中缀表达式转化为后缀表达示和前述对中缀表达式求值的方法完全类似,但只需要运 算符栈,遇到运算对象时直接放后缀表达式的存储区,假设中缀表达式本身合法且在字符数组 A 中,转换后的后缀表达式存储在字符数组 B 中。
具体做法:遇到运算对象顺序向存储后缀表达式的 B数组中存放,遇到运算符时类似于中缀表达式求值时对运算符的处理过程,但运算符出栈后不是进行相应的运算,而是将其送入B 中存放。
3、栈与递归
在高级语言编制的程序中,调用函数与被调用函数之间的链接和信息交换必须通过栈进行。当在一个函数的运行期间调用另一个函数时,在运行该被调用函数之前,需先完成三件事:
(1)将所有的实在参数、返回地址等信息传递给被调用函数保存;
(2)为被调用函数的局部变量分配存储区;
(3)将控制转移到被调用函数的入口。
从被调用函数返回调用函数之前,应该完成:
(1)保存被调函数的计算结果;
(2)释放被调函数的数据区;
(3)依照被调函数保存的返回地址将控制转移到调用函数。
多个函数嵌套调用的规则是:后调用先返回,此时的内存管理实行“栈式管理”。
递归函数的调用类似于多层函数的嵌套调用,只是调用单位和被调用单位是同一个函数而已。
将递归程序转化为非递归程序时常使用栈来实现。
递归与非递归转换
1. 递归算法到非递归算法的转换
递归算法具有两个特性:
①递归算法是一种分而治之、把复杂问题分解为简单问题的求解问题方法, 对求解某些复杂问题,递归算法的分析方法是有效的。
②递归算法的效率较低。 为此,在求解某些问题时,希望用递归算法分析问题,用非递归算法求解具体问 题。
(1)消除递归的原因:
其一,有利于提高算法时空性能,因为递归执行时需要系统提供隐式栈实现 递归,效率较低。
其二,无应用递归语句的语言设施环境条件,有些计算机语言不支持递归功 能,如 FORTRAN 语言中无递归机制 。
其三,递归算法是一次执行完,中间过程对用户不可见,这在处理有些问题 时不合适,也存在一个把递归算法转化为非递归算法的需求。
常用的两类消除递归方法:
一类是简单递归问题的转换,对于尾递归和单向递归的算法,可用循环结构 的算法替代。
另一类是基于栈的方式,即将递归中隐含的栈机制转化为由 用户直接控制的 明显的栈。利用堆栈保存参数,由于堆栈的后进先出特性吻合递归算法的执行过 程,因而可以用非递归算法替代递归算法。
(2) 简单递归的消除
在简单情况下,可以将递归算法转化为线性操作序列,直接用循环实现。
①单向递归
单向递归是指递归函数中虽然有一处以上的递归调用语句,但各次递归调用语句 的参数只和主调用函数有关,相互之间参数无关,并且这些递归调用语句处于算法的最后。 计算斐波那契数列的递归算法 Fib(n) 是单向递归的一个典型例子。
②尾递归
尾递归是指递归调用语句只有一个,而且是处于算法的最后,尾递归是单向递归的特例。 以阶乘问题的递归算法 Fact(n)为例讨论尾递归算法的运行过程。