题目:在直角坐标系中给定 p1,p2,p3构成三角形,给定p4可能在三角形边上也可能不在,
问能不能在三角形上找出p5,使得线段p4p5,平分三角形(p4必须在三角形上)。不能则输出-1.
思路:四个点,三条边,三条边的长度,和代码的数据一一对应存储。
①:不在三角形上
②:在三角形上
①在顶点上(两条线段上)
②不在顶点上(一条线段上)
①在中点
②不在中点
最麻烦的就是p4只存在于一条边上。
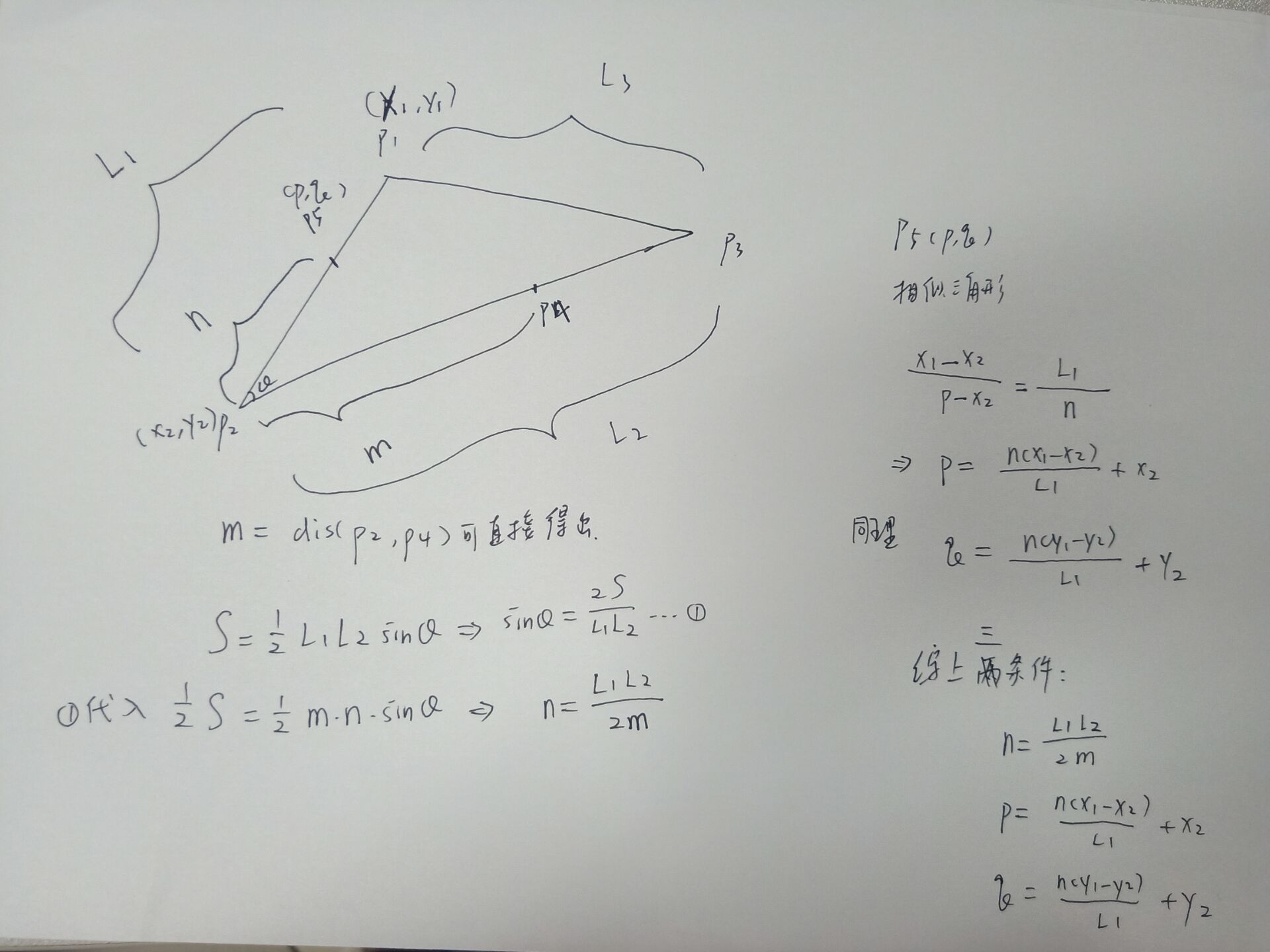
代码:
1 #include<bits/stdc++.h> 2 using namespace std; 3 4 const double eps = 1e-6; 5 int sgn(double x) 6 { 7 if(fabs(x) < eps)return 0; 8 if(x < 0)return -1; 9 else return 1; 10 } 11 struct Point 12 { 13 double x,y; 14 Point(){} 15 Point(double _x,double _y) 16 { 17 x = _x;y = _y; 18 } 19 Point operator -(const Point &b)const 20 { 21 return Point(x - b.x,y - b.y); 22 } 23 24 double operator ^(const Point &b)const//叉积 25 { 26 return x*b.y - y*b.x; 27 } 28 29 double operator *(const Point &b)const//点积 30 { 31 return x*b.x + y*b.y; 32 } 33 void transXY(double B)//绕原点旋转角度B(弧度值),后x,y的变化 34 { 35 double tx = x,ty = y; 36 x = tx*cos(B) - ty*sin(B); 37 y = tx*sin(B) + ty*cos(B); 38 } 39 void read(double a,double b){ 40 x = a; y = b; 41 } 42 }; 43 struct Line 44 { 45 Point s,e; 46 Line(){} 47 Line(Point _s,Point _e) 48 { 49 s = _s;e = _e; 50 } 51 pair<int,Point> operator &(const Line &b)const 52 { 53 //两直线相交求交点 54 //第一个值为0表示直线重合,为1表示平行,为0表示相交,为2是相交 55 //只有第一个值为2时,交点才有意义 56 Point res = s; 57 if(sgn((s-e)^(b.s-b.e)) == 0) 58 { 59 if(sgn((s-b.e)^(b.s-b.e)) == 0) 60 return make_pair(0,res);//重合 61 else return make_pair(1,res);//平行 62 } 63 double t = ((s-b.s)^(b.s-b.e))/((s-e)^(b.s-b.e)); 64 res.x += (e.x-s.x)*t; 65 res.y += (e.y-s.y)*t; 66 return make_pair(2,res); 67 } 68 void read(Point& a,Point& b){ 69 s.x = a.x; 70 s.y = a.y; 71 e.x = b.x; 72 e.y = b.y; 73 } 74 }; 75 bool OnSeg(Point& P,Line& L)//判断点在线段上 76 { 77 return 78 sgn((L.s-P)^(L.e-P)) == 0 && 79 sgn((P.x - L.s.x) * (P.x - L.e.x)) <= 0 && 80 sgn((P.y - L.s.y) * (P.y - L.e.y)) <= 0; 81 } 82 //线长 83 inline double get_Ldis(Line& L){ 84 return sqrt((L.s.x-L.e.x)*(L.s.x-L.e.x)+(L.s.y-L.e.y)*(L.s.y-L.e.y)); 85 } 86 //两点长 87 inline double get_pdis(Point& a,Point& b){ 88 return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y)); 89 } 90 91 inline void print(Line& L){ 92 printf("%.12f %.12f ",(L.s.x+L.e.x)/2,(L.s.y+L.e.y)/2); 93 } 94 95 inline double fun(double n,double x1,double x2,double d){ 96 return n*(x1-x2)/d + x2; 97 } 98 Point p[5]; Line L[5]; double d[5]; 99 inline void solve(Line& l,double m1,double m2,Point& p1,Point& p2,Point& p3,double d1,double d2,double d3){ 100 101 double n; 102 double x,y; 103 if(m1==m2) {printf("%.12f %.12f ",p1.x,p1.y); return;} 104 else if( m1 > m2){ 105 n = (d1*d2)/(2*m1); 106 x = fun(n,p1.x,p2.x,d1); 107 y = fun(n,p1.y,p2.y,d1); 108 } 109 else{ 110 n = (d2*d3)/(2*m2); 111 x = fun(n,p1.x,p3.x,d3); 112 y = fun(n,p1.y,p3.y,d3); 113 } 114 printf("%.12f %.12f ",x,y); 115 } 116 117 int main() 118 { 119 120 int T; 121 double m1,m2; 122 scanf("%d",&T); 123 while(T--){ 124 scanf("%lf%lf%lf%lf%lf%lf%lf%lf",&p[1].x,&p[1].y,&p[2].x,&p[2].y,&p[3].x,&p[3].y,&p[4].x,&p[4].y); 125 L[1].read(p[1],p[2]); L[2].read(p[2],p[3]); L[3].read(p[3],p[1]); 126 for(int i = 1; i <= 3; ++i) d[i] = get_Ldis(L[i]); 127 128 if(OnSeg(p[4],L[1]) || OnSeg(p[4],L[2]) || OnSeg(p[4],L[3])){ 129 if(OnSeg(p[4],L[1]) && OnSeg(p[4],L[2])){ 130 print(L[3]); continue; 131 } 132 if(OnSeg(p[4],L[1]) && OnSeg(p[4],L[3])){ 133 print(L[2]);continue; 134 } 135 if(OnSeg(p[4],L[2]) && OnSeg(p[4],L[3])){ 136 print(L[1]);continue; 137 } 138 if(OnSeg(p[4],L[2])){ 139 m1 = get_pdis(p[2],p[4]); 140 m2 = d[2] - m1; 141 solve(L[2],m1,m2,p[1],p[2],p[3],d[1],d[2],d[3]); 142 continue; 143 } 144 if(OnSeg(p[4],L[1])){ 145 m1 = get_pdis(p[1],p[4]); 146 m2 = d[1] - m1; 147 solve(L[1],m1,m2,p[3],p[1],p[2],d[3],d[1],d[2]); 148 continue; 149 } 150 if(OnSeg(p[4],L[3])){ 151 m1 = get_pdis(p[3],p[4]); 152 m2 = d[3] - m1; 153 solve(L[3],m1,m2,p[2],p[3],p[1],d[2],d[3],d[1]); 154 continue; 155 } 156 printf("-1 "); 157 } 158 else printf("-1 "); 159 } 160 161 return 0; 162 }