孩子上午上课睡着了 。。。自学一会
前言
卡特兰数是一个数列,有时出现在组合数学问题中
一般情况下卡特兰数从第1位开始(第零位为1):1,1,5,14 ,42, 132, 429,1430....
对于卡特兰数有个网格图模型,从中可以得到重要公式:(因为我从别人oj上盗的图所以就是[n,m]的,但是实际上应该是[n,n]的)
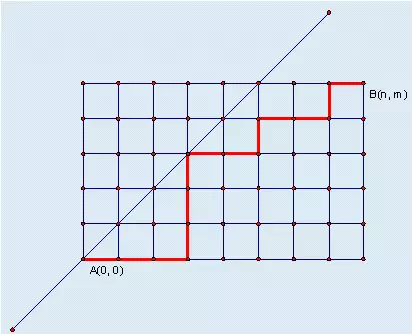
对于上面这个图来说,走到[n,n]但又不越过y=x的方案数即为第n个卡特兰数,
有那种栈的解释,但图更好直观理解。
明显走到[n,n]而不考虑越界的方案数有C(2n,n)种,排除的话,可以考虑转化,
对于每条越过y=x的路径,第一次越出之后的部分全都沿着y=x+1对称翻转,得到等效的路径,
而且这些路径的方案数可以直接计算为从(0,0)走到(n-1,n+1),即C(2n,n-1)
合法的路径数即为C(2n,n)-C(2n,n-1),得到第一个重要公式,即f[n] = C(2n,n) - C(2n,n-1);
同时你可以A一道题叫做bzoj3907
#include<bits/stdc++.h> using namespace std ; struct Node{ int data[2000],len; memset(data,0,sizeof data); len = 0; }a; const int base = 10; Node operator * (Node a,int b){ for(int i=1;i<=a.len;i++){ a.data[i] *= b; a.data[i+1] += a.data[i]/base a.data[i] %= base; } while(a.data[a.len+1]){ ++a.len; a.data[a.len+1] += a.data[a.len]/base; a.data[a.len] %= base; } return a; } Node operator / (Node a,int b) { int res=0; for(int i=a.len;i>=1;i--){ res = res*base + a.data[i]; a.data[i] = res/base; res %= base; } while(!a.data[a.len]) a.len--; return a; } Node operator - (Node a,Node b){ int upl = max(a.len,b.len); for(int i=1;i<=upl;i++){ if(a.data[i] < b.data[i]){ a.data[i]+=base; --a.data[i+1]; } a.data[i]-=b.data[i]; } return a; } int main(){ ios::sync_with_stdio(false); cin>>n>>m; for(int i=1;i<=m;i++){ } }