汉诺塔问题

---恢复内容开始---

汉诺塔的来源

     相传在古印度圣庙中，有一种被称为汉诺塔(Hanoi)的游戏。该游戏是在一块铜板装置上，有三根杆(编号A、B、C)，在A杆自下而上、由大到小按顺序放置64个金盘(如下图)。游戏的目标：把A杆上的金盘全部移到C杆上，并仍保持原有顺序叠好。操作规则：每次只能移动一个盘子，并且在移动过程中三根杆上都始终保持大盘在下，小盘在上，操作过程中盘子可以置于A、B、C任一杆上。

代码

n=eval(input())
def move(n,a,b,c):
    if n==1:
        print(a,'-->',c)
    else:
        move(n-1,a,c,b)
        print(a,'-->',c)
        move(n-1,b,a,c)
move(n,'A','B','C')

运行结果

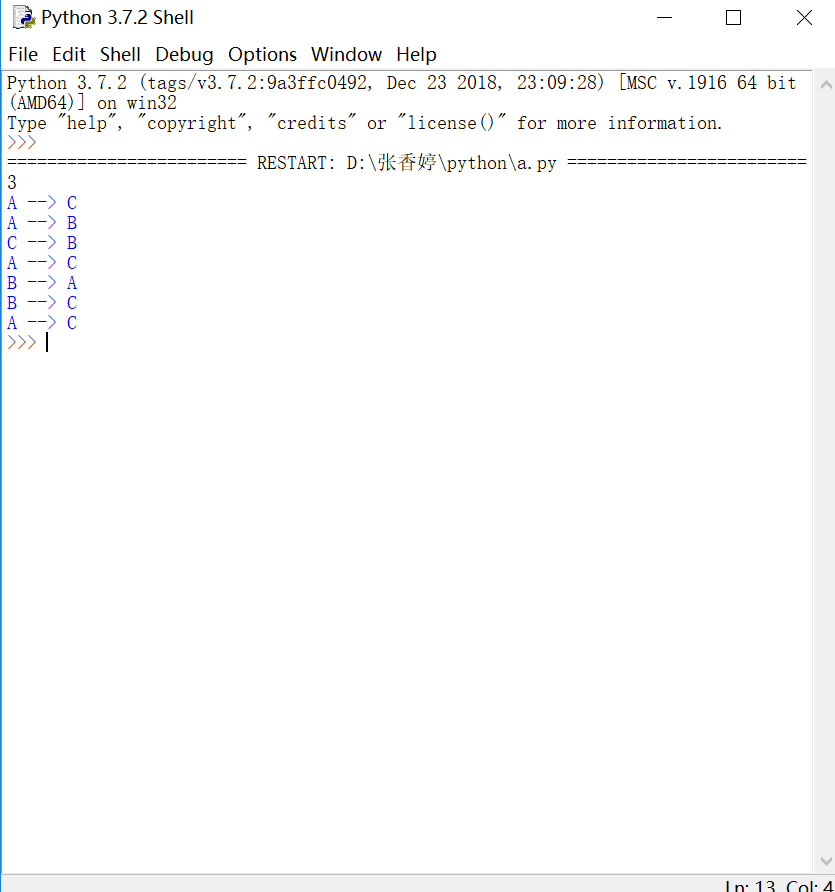
动画代码

import turtle
 
class Stack:
    def __init__(self):
        self.items = []
    def isEmpty(self):
        return len(self.items) == 0
    def push(self, item):
        self.items.append(item)
    def pop(self):
        return self.items.pop()
    def peek(self):
        if not self.isEmpty():
            return self.items[len(self.items) - 1]
    def size(self):
        return len(self.items)
 
def drawpole_3():#画出汉诺塔的poles
    t = turtle.Turtle()
    t.hideturtle()
    def drawpole_1(k):
        t.up()
        t.pensize(10)
        t.speed(100)
        t.goto(400*(k-1), 100)
        t.down()
        t.goto(400*(k-1), -100)
        t.goto(400*(k-1)-20, -100)
        t.goto(400*(k-1)+20, -100)
    drawpole_1(0)#画出汉诺塔的poles[0]
    drawpole_1(1)#画出汉诺塔的poles[1]
    drawpole_1(2)#画出汉诺塔的poles[2]
 
def creat_plates(n):#制造n个盘子
    plates=[turtle.Turtle() for i in range(n)]
    for i in range(n):
        plates[i].up()
        plates[i].hideturtle()
        plates[i].shape("square")
        plates[i].shapesize(1,8-i)
        plates[i].goto(-400,-90+20*i)
        plates[i].showturtle()
    return plates
 
def pole_stack():#制造poles的栈
    poles=[Stack() for i in range(3)]
    return poles
 
def moveDisk(plates,poles,fp,tp):#把poles[fp]顶端的盘子plates[mov]从poles[fp]移到poles[tp]
    mov=poles[fp].peek()
    plates[mov].goto((fp-1)*400,150)
    plates[mov].goto((tp-1)*400,150)
    l=poles[tp].size()#确定移动到底部的高度（恰好放在原来最上面的盘子上面）
    plates[mov].goto((tp-1)*400,-90+20*l)
 
def moveTower(plates,poles,height,fromPole, toPole, withPole):#递归放盘子
    if height >= 1:
        moveTower(plates,poles,height-1,fromPole,withPole,toPole)
        moveDisk(plates,poles,fromPole,toPole)
        poles[toPole].push(poles[fromPole].pop())
        moveTower(plates,poles,height-1,withPole,toPole,fromPole)
 
myscreen=turtle.Screen()
drawpole_3()
n=int(input("请输入汉诺塔的层数并回车:
"))
plates=creat_plates(n)
poles=pole_stack()
for i in range(n):
    poles[0].push(i)
moveTower(plates,poles,n,0,2,1)
myscreen.exitonclick()

动画示意图

---恢复内容结束---