[ CodeForces 1063 B ] Labyrinth

(\)

(Description)

---

给出一个四联通的(N imes M) 网格图和起点。图中有一些位置是障碍物。

现在上下移动步数不限，向左至多走 (a) 步，向右至多走 (b) 步，求从起点出发能到达多少个空地。

• (N,Mle 2000)

(\)

(Solution)

---

爷们太神了......

开始的想法是直接跑最短路， (dist) 为横向移动总步数。

后来发现矛盾在于，如果到一个格子向左走的步数较少，向右走的步数较多，和这种情况反过来，无法确定那种更优，进而无法确定用那种状态更新接下来的点。

然后听爷们讲了好久听懂了正确性证明。考虑要从起点 U 到达 V 这个格子，它横向的差值为 (2) 是固定的。

也就是说，任何一个合法的方案向左走的步数减掉向右走的步数都应该等于 (2)。

那么这种矛盾不存在了。因为向左向右的步数会同时增长，否则一定不会到达这个目标点。

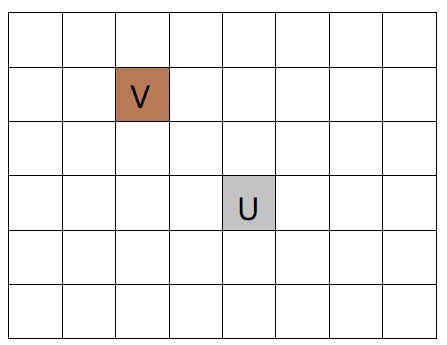
然后就愉快上最短路，根据(Dij) 的原理，循环次数就是访问的点数。

(\)

(Code)

---

#include<cmath>
#include<queue>
#include<cstdio>
#include<cctype>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 2010
#define R register
#define gc getchar
#define inf 2000000000
using namespace std;
typedef long long ll;

inline ll rd(){
  ll x=0; bool f=0; char c=gc();
  while(!isdigit(c)){if(c=='-')f=1;c=gc();}
  while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=gc();}
  return f?-x:x;
}

int n,m,lx,rx,ux,uy,ans;

bool mp[N][N],vis[N][N];

struct dist{
  int x,y,l,r,sum;
  friend operator < (const dist &x,const dist &y){
    return x.sum>y.sum;
  }
}dis[N][N];

priority_queue<dist> q;

int main(){
  n=rd(); m=rd();
  ux=rd(); uy=rd();
  lx=rd(); rx=rd();
  char c=gc();
  for(R int i=1;i<=n;++i)
    for(R int j=1;j<=m;++j){
      while(c!='.'&&c!='*') c=gc();
      mp[i][j]=(c=='.');
      c=gc();
      dis[i][j].x=i; dis[i][j].y=j;
      dis[i][j].l=dis[i][j].r=dis[i][j].sum=inf;
    }
  dis[ux][uy].l=dis[ux][uy].r=dis[ux][uy].sum=0;
  q.push(dis[ux][uy]);
  while(!q.empty()){
    dist x=q.top(); q.pop();
    if(vis[x.x][x.y]) continue;
    vis[x.x][x.y]=1; ++ans;
    if(mp[x.x+1][x.y]){
      if(dis[x.x+1][x.y].sum>x.sum){
        dis[x.x+1][x.y].l=x.l;
        dis[x.x+1][x.y].r=x.r;
        dis[x.x+1][x.y].sum=x.sum;
        q.push(dis[x.x+1][x.y]);
      }
    }
    if(mp[x.x-1][x.y]){
      if(dis[x.x-1][x.y].sum>x.sum){
        dis[x.x-1][x.y].l=x.l;
        dis[x.x-1][x.y].r=x.r;
        dis[x.x-1][x.y].sum=x.sum;
        q.push(dis[x.x-1][x.y]);
      }
    }
    if(mp[x.x][x.y-1]&&x.l<lx){
      if(dis[x.x][x.y-1].sum>x.sum+1){
        dis[x.x][x.y-1].l=x.l+1;
        dis[x.x][x.y-1].r=x.r;
        dis[x.x][x.y-1].sum=x.sum+1;
        q.push(dis[x.x][x.y-1]);
      }
    }
    if(mp[x.x][x.y+1]&&x.r<rx){
      if(dis[x.x][x.y+1].sum>x.sum+1){
        dis[x.x][x.y+1].l=x.l;
        dis[x.x][x.y+1].r=x.r+1;
        dis[x.x][x.y+1].sum=x.sum+1;
        q.push(dis[x.x][x.y+1]);
      }
    }
  }
  printf("%d
",ans);
  return 0;
}