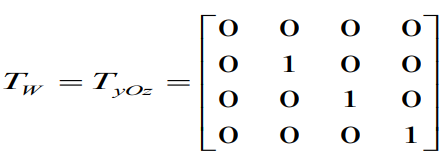三维物体几何变换
同二维变换一样,三维基本几何变换都是相对于坐标原点和坐标轴j进行的几何变换:有平移、比例、旋转、对称和错切等
与二维变换类似,引入齐次坐标表示,即:三维空间中的某点变换可以表示成点的齐次坐标与四阶的三维便变换矩阵相乘
1、平移变换:若三维物体沿 x、y、z 方向上移动一个位置,而物体的大小和形状均不变,则称为平移变换。平移变换矩阵如下:

2、比例变换:比例变换分局部比例变换和整体比例变换
局部比例变换:局部比例变换由变换矩阵中主对角线元素决定,其他元素均为零。当对 x、y、z 方向分别进行比例变换时,其变换的矩阵表示为:
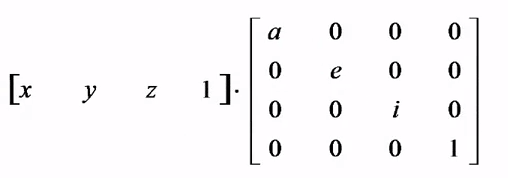
整体比例变换:整体比例变换可用以下矩阵表示,即 x、y、z 方向上的比例变换倍数相同。

3、旋转变换:三维立体的旋转变换是指给定的三维立体绕三位空间某个制定的坐标轴旋转θ角度,旋转后立体的空间位置将发生变化,但形状不变。θ角的正负按右手规则确定,右手大拇指指向旋转轴的正向,其余四个手指指向θ的正方向。
(1)绕 z 轴旋转:三维立体上的 x、y 坐标发生变换而 z 坐标不变。
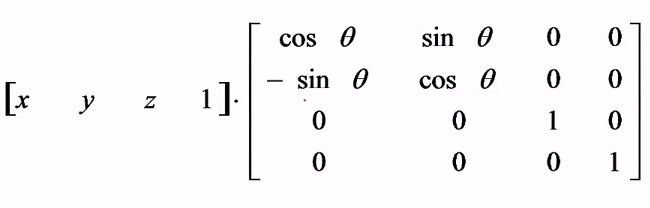
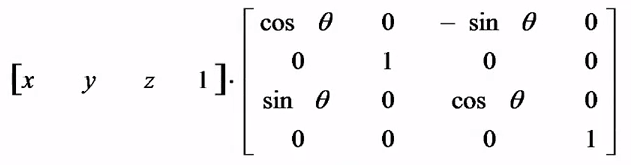
(2)绕 x 轴旋转:
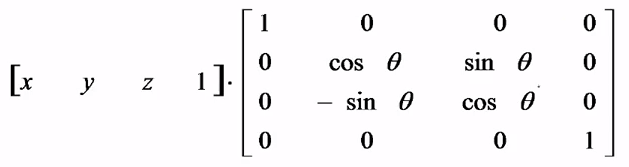
(3)绕 y 轴旋转:
(4)绕任意轴旋转:将绕任意轴旋转的问题变换为绕坐标轴旋转的问题。
4、对称变换:三维物体对称变换有关于坐标平面、坐标轴的对称变换。
三维物体投影变换 —— 如何在二维平面上显示三维物体
1、中心(透视)投影:投影线均通过投影中心。在投影中心相对于投影面确定的情况下,空间的一个点在投影面上只存在唯一一个投影。
2、平行投影:如果把透视投影的中心移至无穷远,则各投影线称为相互平行的直线,这种投影法称为平行投影。根据投影方向与投影面的夹角可分为正投影法和斜投影法。
正投影根据投影面与坐标轴的夹角又可以分为两类:三视图和正轴侧图
当投影面与某一坐标轴垂直的时候,得到的投影为三视图,这时投影方向与这个坐标轴的方向一致;否则,得到的投影为轴侧图。
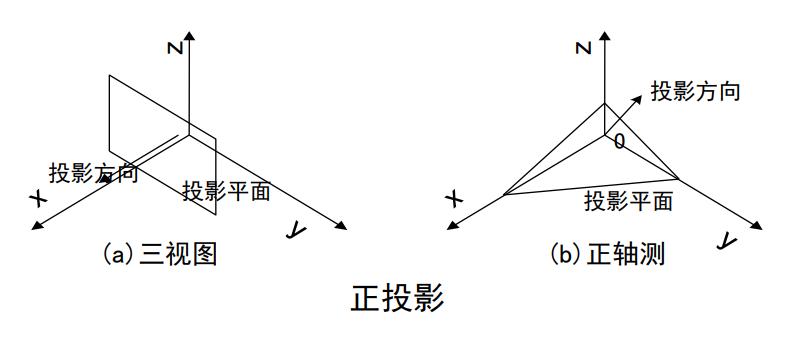
三视图的计算(算法步骤):
a、确定三维物体上各点的位置坐标;
b、引入齐次坐标,求出所作变换相应的变换矩阵;
c、将所作变换用矩阵表示,通过运算求得三维物体上各店经变换后的点坐标值;
d、由变换后得到的二维点绘出三维物体投影后的三视图。
主视图:将三维物体xOz面(又称V面)作垂直投影,得到主视图。由投影变换前后三维物体上点到主视图上点的关系,此投影变换的矩阵为:
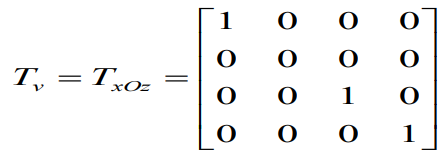
俯视图:将三维物体xOy面(又称H面)作垂直投影得到俯视图。此投影的变换矩阵为:

侧视图:将三维物体yOz面(又称W面)作垂直投影得到侧视图。此投影的变换矩阵为: