向量的一些基本概念
向量的相加和数乘
向量的线性组合
仿射组合:如果线性组合的系数a1,a2,...am的和等于1,那么它就是仿射组合,即 a1 + a2 + ... + am = 1
凸组合:满足仿射组合的条件,且 ai >= 0 (i = 1,2,...,m)
向量的度量和单位向量
向量的点积与叉积
计算机图形学中坐标系的分类
1、世界坐标系:世界坐标系是一个公共坐标系,是现实中物体或场景的统一参照系。计算机图形系统中涉及的其他坐标系都是参照它进行定义的。
2、建模坐标系(局部坐标系):每个物体(对象)有它自己的局部中心和坐标系。
3、观察坐标系:主要用于从观察者的角度对整个世界坐标系内的对象进行重新定位和描述。
4、设备坐标系:适合特定输出设备输出对象的坐标系。设备坐标一般都是整数。
5、规范化坐标系:规范化坐标系独立于设备,能容易地转变为设备坐标系,是一个中间坐标系。
二维图形变化
齐次坐标:用三维向量表示二维向量,或者一般而言,用一个n+1维的向量表示一个n维向量的方法称为齐次坐标表示法。
为什么要引入齐次坐标:在笛卡尔坐标系内,向量(x, y)是位于z=0的平面上的点;而向量(x, y, 1)是位于z=1的高平面上的点。对于图形来说,两者并没有实质性的差别,但是却给后面的矩阵运算提供了可行性和方便性。
基本几何变换:指对图形的几何信息经过平移、比例、旋转等变换后产生的新图形。
1、平移变换:将某个点沿直线路径从一个坐标位置移到另一个坐标位置的重定位过程,即新的坐标在x方向和y方向上增加了一个增量和。
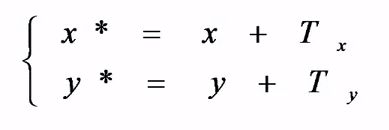
将以上式子写成矩阵的形式就是:

2、比例变换:是指点相对于坐标原点沿x方向放缩Sx倍,沿y方向放缩Sy倍。其中Sx和Sy称为比例系数。比例变换的齐次坐标计算形式如下:
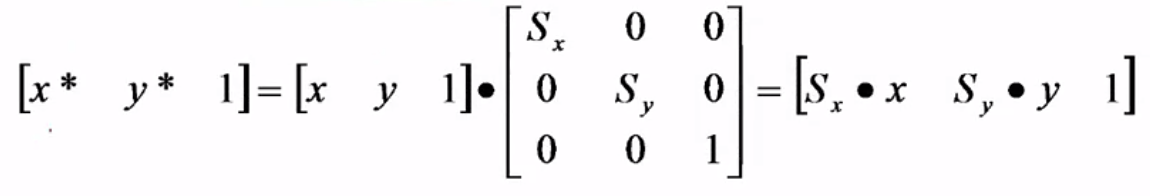
3、对称变换:也称为反射变换或镜像变换,变换后的图形是原图关于某一轴线或原点的镜像。
a)关于x轴对称:(x, y)——>(x, -y)
b)关于y轴对称:(x, y)——>(-x, y)
4、旋转变换:二维旋转是指将p点绕坐标原点转动某个角度α(逆时针为正,顺时针为负)得到新的点p*的重定位过程。
其变换矩阵和推导过程参见:计算机图形学导论作业1
5、错切变换:在图形学的应用中,有时需要产生弹性物体的变形处理,这就需要用到错切变换。x值或者y值越小,错切量越小;x值或者y值越大,错切量越大。参见:错切变换
复合变换:是指图形作一次以上的几何变换 ,变换的结果是每次的变换矩阵相乘
1、二维复合平移
2、二维复合比例平移
3、二维复合旋转
注:复合变换的结果是将两次或多次变换的变换矩阵相乘,需要注意的是矩阵相乘的顺序不可交换
坐标系之间的变换
图形变换经常需要从一个坐标系变换到另一个坐标系
首先考虑将两个坐标系做复合变换,可以分两步来进行:
1)将一个坐标系的坐标原点平移至另一个坐标系的原点——平移变换
2)将一个坐标系的x轴旋转到另一个坐标系的x轴上——旋转变换
上诉变换步骤可以用变换矩阵表示:
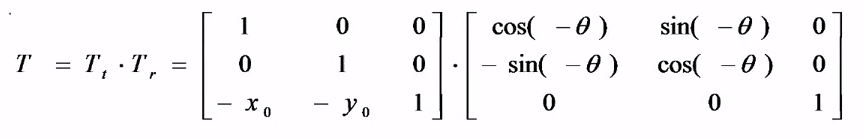
相对任意参考点的二维几何变换
比例、旋转变换等均与参考点相关。如要对某个参考点做二维几何变换,其变换过程如下
a、将固定点移动至坐标原点,此时进行平移变换;
b、针对原点进行二维几何变换;
c、进行反平移,将固定点又移回到原来的位置。
二维变换矩阵分析
