题意:
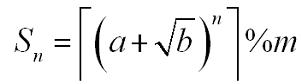
思路:
直接拿别人的图,自己写太麻烦了~
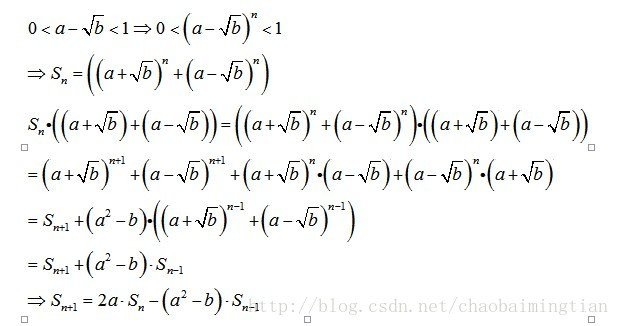
然后就可以用矩阵快速幂套模板求递推式啦~
另外:
这题想不到或者不会矩阵快速幂,根本没法做,还是2013年长沙邀请赛水题,也是2008年Google Codejam Round 1A的C题。
#include <bits/stdc++.h>
typedef long long ll;
const int N = 5;
int a, b, n, mod;
/*
*矩阵快速幂处理线性递推关系f(n)=a1f(n-1)+a2f(n-2)+...+adf(n-d)
*/
struct Matrix {
int row, col;
ll arr[N][N];
Matrix(int r=0, int c=0) {
row = r; col = c;
memset (arr, 0, sizeof (arr));
}
Matrix operator * (const Matrix &B) {
Matrix ret(row, B.col);
for (int i=0; i<row; ++i) {
for (int j=0; j<B.col; ++j) {
for (int k=0; k<col; ++k) {
ret.arr[i][j] = (ret.arr[i][j] + (ll) arr[i][k] * B.arr[k][j]) % mod;
}
}
}
return ret;
}
void unit(int n) {
row = col = n;
for (int i=0; i<n; ++i) {
arr[i][i] = 1;
}
}
};
Matrix operator ^ (Matrix X, ll n) {
Matrix ret; ret.unit (X.col);
while (n) {
if (n & 1) {
ret = ret * X;
}
X = X * X;
n >>= 1;
}
return ret;
}
int f[3], x[3];
int main() {
while (scanf ("%d%d%d%d", &a, &b, &n, &mod) == 4) {
double c = (double) a + sqrt ((double) b);
f[1] = ((ll) ceil (c)) % mod;
f[2] = ((ll) ceil (c*c)) % mod;
int d = 2;
x[1] = (2*a) % mod; x[2] = (-(a*a-b) % mod + mod) % mod;
if (n <= d) {
printf ("%d
", f[n]);
} else {
Matrix Fn(d+1, d+1), Fd(d+1, 1);
for (int i=0; i<Fn.row-1; ++i) {
Fn.arr[i][i+1] = 1;
}
for (int i=1; i<Fn.col; ++i) {
Fn.arr[Fn.row-1][i] = x[d-i+1];
}
for (int i=0; i<Fd.row; ++i) {
Fd.arr[i][0] = f[i];
}
Fn = Fn ^ (n - d);
Fn = Fn * Fd;
printf ("%d
", Fn.arr[d][0]);
}
}
return 0;
}