Codeforces Round #346 (Div. 2)

前三题水

Ａ

#include <bits/stdc++.h>

typedef long long ll;
const int N = 1e5 + 5;


int main() {
    int n, a, b; std::cin >> n >> a >> b;
    int bb = b;
    if (b < 0) bb = -b;
    while (bb--) {
        if (b < 0) {
            a--;
        } else {
            a++;
        }
        if (a == 0) {
            a = n;
        } else if (a == n + 1) {
            a = 1;
        }
    }
    std::cout << a << '
';

    return 0;
}

Ｂ

#include <bits/stdc++.h>

typedef long long ll;
const int M = 1e4 + 5;
struct Info {
    std::string name;
    int score;
    bool operator < (const Info &rhs) const {
        return score > rhs.score;
    }
};
std::vector<Info> vec[M];

bool same_three(int a, int b, int c) {
    return b == c;
}

bool same(int id) {
    return same_three (vec[id][0].score, vec[id][1].score, vec[id][2].score);
}

int main() {
    int n, m; std::cin >> n >> m;
    std::string str; int num, score;
    for (int i=0; i<n; ++i) {
        std::cin >> str >> num >> score;
        vec[num].push_back ((Info) {str, score});
    }
    for (int i=1; i<=m; ++i) {
        if (vec[i].size () < 2) {
            puts ("?");
            continue;
        } else {
            std::sort (vec[i].begin (), vec[i].end ());
            if (vec[i].size () > 2 && same (i)) {
                puts ("?");
            } else {
                std::cout << vec[i][0].name << " " << vec[i][1].name << '
';
            }
        }
    }

    return 0;
}

Ｃ

#include <bits/stdc++.h>

typedef long long ll;
const int N = 1e5 + 5;
std::map<int, bool> vis;

int main() {
    int n, m; scanf ("%d%d", &n, &m);
    for (int a, i=0; i<n; ++i) {
        scanf ("%d", &a);
        vis[a] = true;
    }
    std::vector<int> vec;
    int now = 1;
    while (m - now >= 0) {
        if (vis[now]) {
            now++;
        } else {
            m -= now;
            vec.push_back (now);
            now++;
        }
    }
    printf ("%d
", vec.size ());
    for (int i=0; i<vec.size (); ++i) {
        printf ("%d%c", vec[i], i == vec.size () - 1 ? '
' : ' ');
    }

    return 0;
}

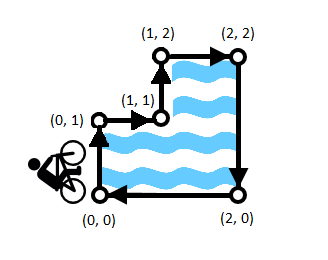
几何(叉积)　D - Bicycle Race

题意：一个人从最下面的位置逆时针沿着湖转一圈，当转角指向湖的方向认为是危险的，问有多少个危险的转角．

分析：分类讨论也就四种情况，但是注意出发点不一定是最左边的(最下面的)；也可以用叉积来判断，大于０表示是顺时针满足危险的定义．

#include <bits/stdc++.h>

typedef long long ll;
const int N = 1e4 + 5;
struct Point {
    int x, y;
};
Point point[N];

int main() {
    int n; scanf ("%d", &n);
    for (int i=0; i<=n; ++i) {
        scanf ("%d%d", &point[i].x, &point[i].y);
    }
    int ans = 0;
    for (int i=0; i<n-2; ++i) {
        if (point[i].x == point[i+1].x) {
            if (point[i+1].y > point[i].y) {
                if (point[i+2].x < point[i+1].x) {
                    ans++;
                }
            } else {
                if (point[i+2].x > point[i+1].x) {
                    ans++;
                }
            }
        } else {
            if (point[i].x < point[i+1].x) {
                if (point[i+1].y < point[i+2].y) {
                    ans++;
                }
            } else {
                if (point[i+1].y > point[i+2].y) {
                    ans++;
                }
            }
        }
    }
    printf ("%d
", ans);

    return 0;
}

#include <bits/stdc++.h>

typedef long long ll;
const int N = 1e4 + 5;
struct Point {
    int x, y;
    Point operator - (const Point &rhs) const {
        return (Point) {x - rhs.x, y - rhs.y};
    }
};
Point point[N];
typedef Point Vector;

int cross(Vector A, Vector B) {
    return A.x * B.y - A.y * B.x;
}

int main() {
    int n; scanf ("%d", &n);
    for (int i=0; i<=n; ++i) {
        scanf ("%d%d", &point[i].x, &point[i].y);
    }
    int ans = 0;
    for (int i=1; i<n; ++i) {
        if (cross (point[i-1] - point[i], point[i+1] - point[i]) < 0) {
            ans++;
        }
    }
    printf ("%d
", ans);

    return 0;
}

图论　E - New Reform

题意：ｎ个点，ｍ条边，每条边是单向的，问如何安排每条边的方向使得入度为０的点最少，最少是几个．

分析：进行ＤＦＳ，如果访问到已访问过的点表示该连通块有环，也就是可以满足每个点的入度大于等于１．

#include <bits/stdc++.h>

const int N = 1e5 + 5;

std::vector<int> G[N];
bool vis[N];
int n, m, add;

void DFS(int u, int fa) {
    if (vis[u]) {
        add = 0;
        return ;
    }
    vis[u] = true;
    for (int i=0; i<G[u].size (); ++i) {
        int v = G[u][i];
        if (v == fa) {
            continue;
        }
        DFS (v, u);
    }
}

int main() {
    scanf ("%d%d", &n, &m);
    for (int i=0; i<m; ++i) {
        int u, v; scanf ("%d%d", &u, &v);
        G[u].push_back (v);
        G[v].push_back (u);
    }
    int ans = 0;
    for (int i=1; i<=n; ++i) {
        if (vis[i]) {
            continue;
        }
        add = 1;
        DFS (i, 0);
        ans += add;
    }
    printf ("%d
", ans);

    return 0;
}

并查集　F - Polycarp and Hay

题意：ｎ＊ｍ的矩阵有不同高度的干草，现要割成高度相同的连通块，且其中至少一个干草的高度没有变化，以及连通块的高度和等于ｋ，求可行的方案．

分析：统计出每个可以高度不变化且被ｋ整除，且连通块数量不小于ｋ/a[i][j]，那么ＢＦＳ一次能的得到方案．按照高度从大到小排序，对于当前的干草累加上周围高度不小于它的连通块数量，ＤＰ思想或者说是求前缀，用并查集维护．

#include <bits/stdc++.h>

typedef long long ll;
const int N = 1e3 + 5;
int dx[] = {-1, 1, 0, 0};
int dy[] = {0, 0, -1, 1};
ll a[N][N];
bool vis[N][N];
int n, m;
ll k, num, aim;

int rt[N*N], rk[N*N];
int Find(int x) {
    return rt[x] == -1 ? x : rt[x] = Find (rt[x]);
}
void Union(int x, int y) {
    x = Find (x);
    y = Find (y);
    if (x == y) {
        return ;
    }
    rt[x] = y;
    rk[y] += rk[x];
}

struct Info {
    ll val;
    int x, y;
    bool operator < (const Info &rhs) const {
        return val > rhs.val;
    }
};
std::vector<Info> vec;

bool judge(int x, int y) {
    if (x < 1 || x > n || y < 1 || y > m) {
        return false;;
    }
    return true;
}

void BFS(int x, int y) {
    std::queue<std::pair<int, int> > que;
    que.push (std::make_pair (x, y));
    vis[x][y] = true; num--;

    while (!que.empty ()) {
        int nx = que.front ().first, ny = que.front ().second;
        que.pop ();
        for (int i=0; i<4; ++i) {
            int tx = nx + dx[i];
            int ty = ny + dy[i];
            if (num == 0) {
                continue;
            }
            if (!judge (tx, ty)) {
                continue;
            }
            if (vis[tx][ty]) {
                continue;
            }
            if (a[tx][ty] < aim) {
                continue;
            }
            vis[tx][ty] = true; num--;
            que.push (std::make_pair (tx, ty));
        }
    }
}

void print() {
    for (int i=1; i<=n; ++i) {
        for (int j=1; j<=m; ++j) {
            if (vis[i][j]) {
                printf ("%I64d ", aim);
            } else {
                printf ("0 ");
            }
        }
        puts ("");
    }
}

int main() {
    scanf ("%d%d%I64d", &n, &m, &k);
    for (int i=1; i<=n; ++i) {
        for (int j=1; j<=m; ++j) {
            scanf ("%I64d", &a[i][j]);
            vec.push_back ((Info) {a[i][j], i, j});
        }
    }
    std::sort (vec.begin (), vec.end ());
    memset (rt, -1, sizeof (rt));
    std::fill (rk, rk+N*N, 1);

    for (int i=0; i<vec.size (); ++i) {
        Info &r = vec[i];
        if (r.val == 0) {
            break;
        }
        for (int j=0; j<4; ++j) {
            int tx = r.x + dx[j];
            int ty = r.y + dy[j];
            if (!judge (tx, ty)) {
                continue;
            }
            if (a[tx][ty] >= r.val) {
                Union ((tx-1)*m+ty, (r.x-1)*m+r.y);
            }
        }
        int fa = Find ((r.x-1)*m+r.y);
        if (k % r.val != 0 || k / r.val > rk[fa]) {
            continue;
        }
        puts ("YES");
        num = k / r.val; aim = r.val;
        BFS (r.x, r.y);
        print ();
        return 0;
    }
    puts ("NO");

    return 0;
}